基于可信度小波神经网络的多传感器数据融合方法
陈 英, 董思羽
(南昌航空大学 软件学院, 南昌 330063)
传感器网络具有收集、 处理和传输数据等功能. 多传感器数据融合技术可提高处理数据的准确性和可靠性, 目前已有许多研究成果: 文献[1]利用支持向量机, 提出了一种异常值检测的隐私保护协议; 文献[2]基于加权融合方法, 提出了一种反馈信任模型计算节点权重的融合方法; 文献[3]利用Kalman滤波算法, 在TEEN(threshold-sensitive energy efficient sensor network protocol)路由协议的基础上提出了一种新的融合方案; 文献[4]考虑多元时空关系, 提出了一种基于多元回归方程的数据融合算法; 文献[5-7]利用Kalman滤波算法对监测数据进行滤波融合; 文献[8]结合距离评价技术和最大关联与最小冗余的耦合特征选择方案获取最优特征集, 提出了一种基于深度结构融合多传感器数据的方案; 文献[9-10]利用神经网络的自组织学习能力和模糊逻辑推理能力进行数据融合, 提高了数据精度; 文献[11]针对无法有效处理证据冲突的问题, 提出了一种基于改进证据理论的融合学习向量化神经网络和决策树的集成诊断模型, 通过进一步决策融合, 实现对轴承的故障诊断; 文献[12]使用粗糙集和反向传播网络, 提高了多传感器处理数据的精度和准确度; 文献[13]提出了自适应的模糊Kalman融合算法, 提高了GPS(global position system)定位数据的精度; 文献[14]提出了一种基于证据的信念发散度测度和信念熵的多传感器数据融合方法, 克服了对高度冲突数据进行融合时可能会出现违反常规结果的情况; 文献[15]利用模糊集对多传感器数据进行融合, 降低了传感器数据的不确定性; 文献[16]基于连续隐Markov模型对运动控制和体感传感器数据进行融合算法设计, 实验结果表明, 该算法能有效降低传感器数据的不确定性, 并在此基础上提出了手语识别框架; 文献[17]利用随机有限集在对多传感器数据进行融合的同时, 对后续的传感器数据也进行了预测. 上述这些单一的数据融合方法可部分达到融合的目的, 但鲁棒性较低, 融合结果缺乏稳定性和准确率. 如: Kalman滤波法不能满足实时性; 小波技术在实际应用中去噪效果较差; 加权均值法虽然实现计算简单, 但实时性较低. 而且部分算法未考虑到时间序列上传感器收集数据的波动性, 未体现数据融合的准确性. 因此, 本文将多种融合技术和方法进行综合运用, 结合小波技术和神经网络的优点, 利用传感器的可信度进行数据融合. 实验结果表明, 本文方法体现了整个时间序列上数据的波动和传感器的稳定性, 提高了数据精确度和融合结果的可靠性.
1 相关理论
1.1 小波阈值去噪
小波变换将包含噪声的信号分解为高频分量和低频分量, 低频分量也称为近似分量. 因为软阈值得到的小波系数连续性较好, 具有使估计信号不产生附加震荡的优点, 所以本文算法选用软阈值进行阈值处理. 若|s|≤λ, 则s=0, 否则s=s-λ, 其中:s为分层后获取的分解系数;λ为设定的阈值. 软阈值处理公式为
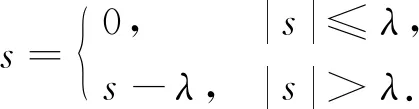
(1)
小波阈值去噪步骤如下:
1)对包含噪声的信号进行小波变换, 通过对信号进行层数分解, 得到一系列小波分解系数;
2) 通过软阈值函数对小波分解系数进行阈值处理, 得到估计小波系数;
3) 利用估计后的小波系数进行小波重构, 重构后的信号即为去噪后信号.
1.2 神经网络
BP神经网络学习过程如下.
1) BP神经网络初始化: 为各连接权值赋予初值, 确定误差函数e、 计算精度ε和最大学习次数M, 采用Sigmoid函数为激励函数.
2) 计算隐含层各神经元的输入uj和输出hj:
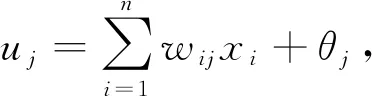
(2)

(3)
其中:θj为隐含层第j个神经元阈值;wij为权重.
3) 计算输出层第k个神经元的输入vk和输出yk:
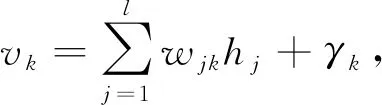
(4)
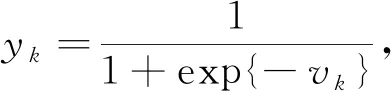
(5)
其中γk为输出层第k个神经元阈值.
4) 计算全局均方误差:
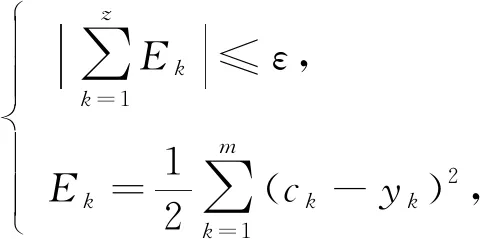
(6)
其中:Ek为均方误差;ε为预设精度.
1.3 可信度融合
将传感器i和j的采样数据si与sj之间差值的绝对值定义为绝对距离disij, 计算公式为
disij=|si-sj|.
(7)
定义1当时间为t时, 传感器i和j的采样数据si与sj的融合程度cij为

(8)
定义2当时间为t时, 样本数据的融合度矩阵为

(9)
定义3当时间为t时, 传感器i的一致融合度ui(t)计算公式为
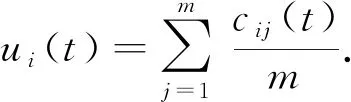
(10)
定义4当时间为t时, 传感器i的分布均衡度τi(t)计算公式为
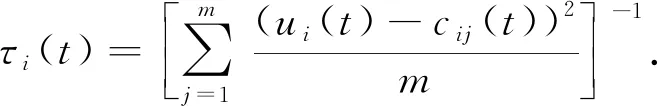
(11)
定义5当时间为t时, 传感器i的可信度系数ωi(t)计算公式为
ωi(t)=ui(t)×τi(t),
(12)
归一化处理后得
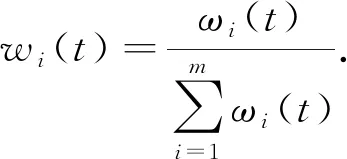
(13)
所以在t时刻, 最终的融合结果表达式用可信度表示为
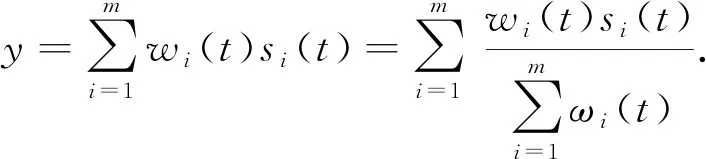
(14)
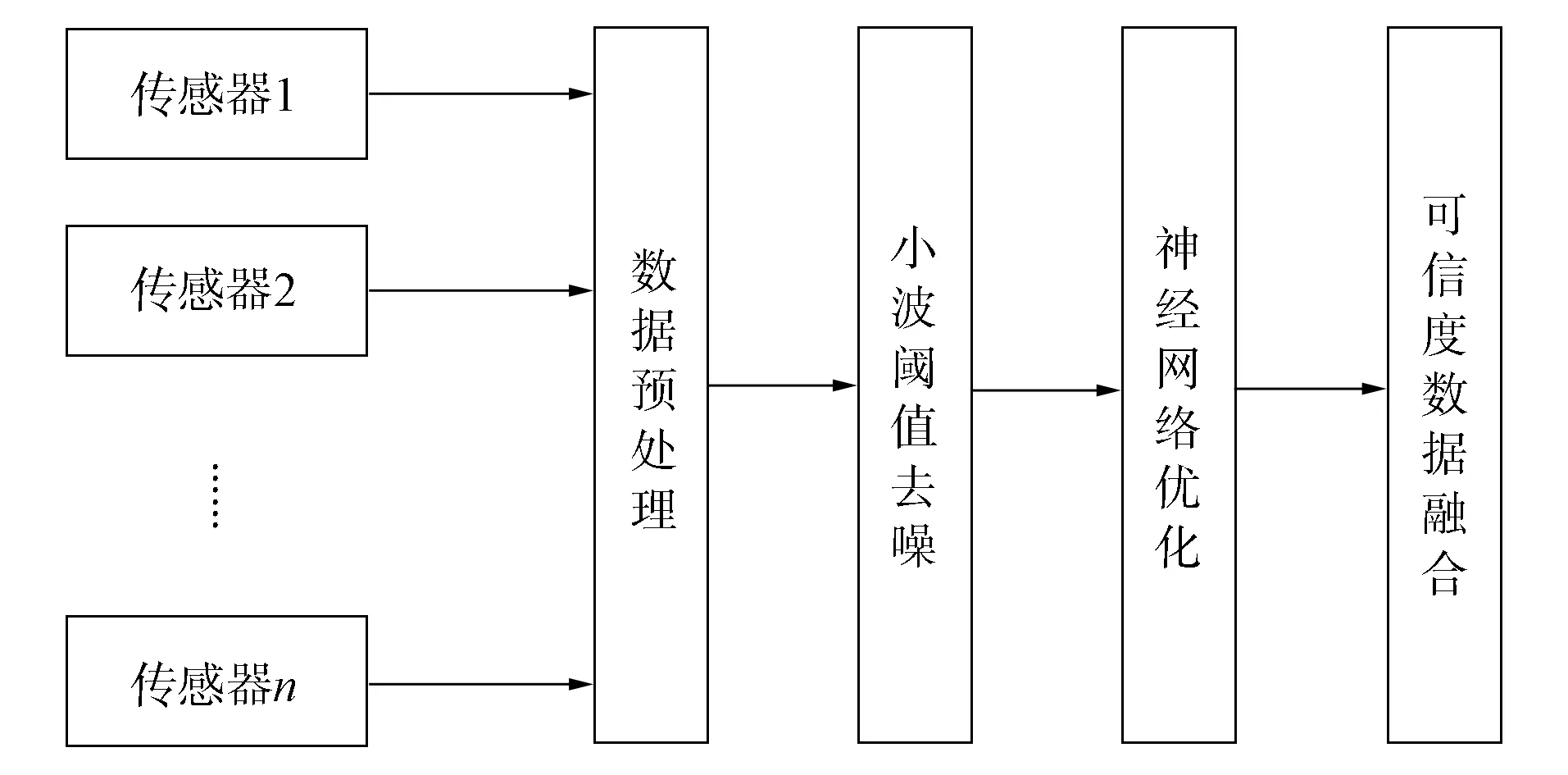
图1 改进融合方法对数据的预处理和融合过程
2 改进的融合方法
本文改进的融合方法对数据的预处理和融合过程如图1所示. 改进融合方法的融合过程步骤如下:
1) 通过拉依达准则等对传感器收集的数据进行预处理, 包括数据的清洗、 替换异常值等;
2) 利用小波阈值去噪对预处理后的数据进行去噪处理, 对小波分层后的高频系数进行阈值处理, 对获取的低频系数使用神经网络进行优化;
3) 对变换和规约后的数据进行神经网络优化;
4) 通过传感器的可信度进行数据融合, 得到最后的融合结果.
2.1 数据预处理
数据预处理主要包括对数据进行野值检测、 缺失值填补和数据转换等, 步骤如下:
1) 对收集数据使用拉依达准则等检测异常数据, 用插值法对异常值或缺失值进行填补;
2) 对更改后的数据值进行归一化处理, 原始数据的归一化关系为
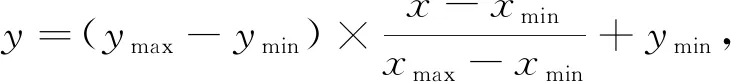
(15)
其中:x为样本原始数据值;xmax,xmin分别为样本原始数据中的最大值和最小值;y为归一化后映射在[ymin,ymax]内的结果值;
3) 得到归一化的样本数据后, 对其进行规约处理, 用较小的数据替换或估计原始数据, 从而减少数据量.
2.2 基于可信度的小波和神经网络融合
基于传感器可信度的小波和神经网络融合步骤如下:
1) 利用小波技术对样本数据进行分层处理, 得到各层的低频系数和高频系数;
2) 先对得到的各部分高频系数进行阈值处理, 然后使用神经网络对低频系数进行优化, 获取优化后的低频系数;
3) 用小波技术处理后的高频系数对优化后的低频系数进行重构;
4) 用样本数据计算各时刻数据的融合度矩阵和传感器的一致融合度, 并利用二者计算出传感器的可信度;
5) 利用神经网络对各传感器数据进行优化处理, 最终通过传感器可信度获得融合结果.
3 实验结果分析
3.1 数据来源
本文的实验数据来源于美国Berkeley-Inter实验室所提供的开放数据集(http://db.csail.mit.edu/labdata/labdata.html), 该数据集共包含约230万条记录, 使用gz格式压缩后的文件大小约为34 MB, 解压缩文件大小约为150 MB; 使用54个Mica2Dot传感器, 传感器的部署位置如图2所示, 所有传感器每31 s进行一次数据采集, 采集的数据包括温度(℃)、 湿度(校正后的相对湿度, 范围为0~100%)、 光照度(lx)和电压(2~3 V), 采集时间为2004-02-28—2004-04-05. 该数据集中某些Mica2Dot的数据存在丢失或截断的情形.
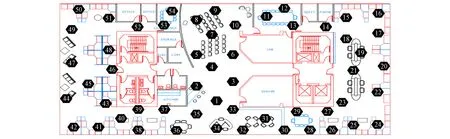
图2 Berkeley-Inter实验室的传感器部署示意图
本文随机选择其中6个传感器收集的部分数据作为实验数据进行分析处理, 样本数据的属性列于表1.

表1 样本数据属性
3.2 数据融合结果
温度、 湿度和光照传感器数据的融合结果如图3所示, 其中: (A),(B),(C)分别为温度、 湿度和光照全部实验数据的融合结果, 横坐标表示时间序列(数据量条数), 一个刻度表示31 s, 纵坐标表示相应时刻所对应的数据值; (D)为放大(A)中编号为1050~1065时间段内16个数据的融合结果, 黄色、 青绿色、 黑色、 绿色、 洋红色、 蓝色线段分别表示传感器节点1~6在1050~1065时间段内采集的数据曲线, 红色曲线表示6个传感器节点在1050~1065时间段内采集数据融合后的曲线; (E)为放大(B)中编号为75~90时间段内16个数据的融合结果, 黄色、 青绿色、 黑色、 绿色、 洋红色、 蓝色线段分别表示传感器节点1~6在75~90时间段内采集的数据曲线, 红色曲线表示6个传感器节点在75~90时间段内采集数据融合后的曲线; (F)为放大(C)中编号为495~510时间段内16个数据的融合结果, 黄色、 青绿色、 黑色、 绿色、 洋红色、 蓝色线段分别表示传感器节点1~6在495~510时间段内采集的数据曲线, 红色曲线表示6个传感器节点在495~510时间段内采集数据融合后的曲线. 由图4可见, 本文的数据融合算法波动性较小, 具有很好的稳健性, 融合结果和原始数据贴近度较高.
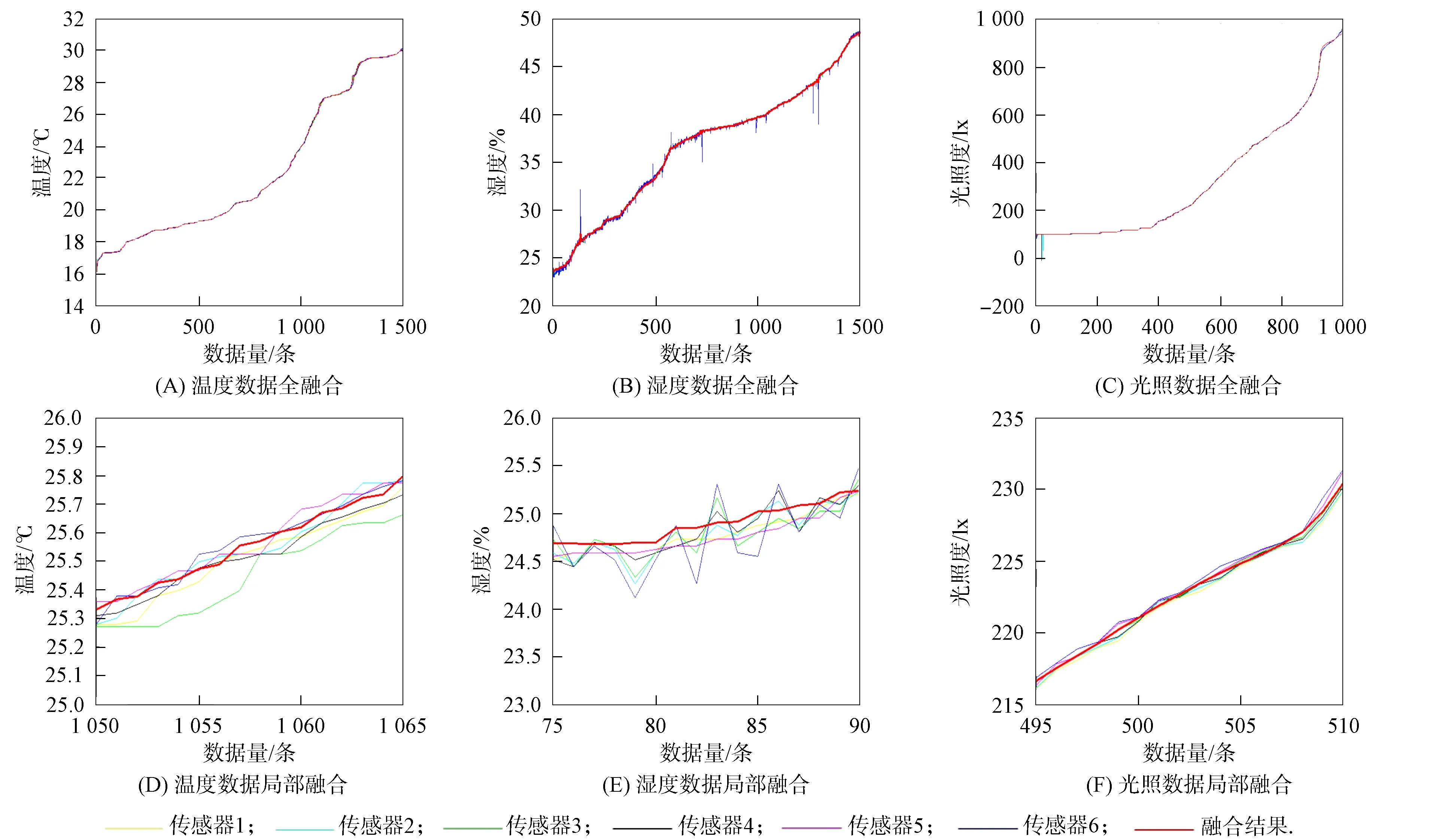
图3 温度、 湿度、 光照数据的融合结果
本文采用均值、 方差、 极差和离散系数等评价指标对4种数据融合算法(本文算法(A), 基于权值的融合方法(B), 基于小波的融合方法(C), 基于Kalman的融合方法(D))的稳健性进行评价. 其中: 方差是衡量一组数据离散程度的度量; 极差表示统计资料中变异量数最大值与最小值之间的差距; 离散系数是测度数据离散程度的相对统计量, 用于比较不同样本数据的离散程度. 上述评价指标的数值越大, 说明融合算法的稳健性越差; 反之, 评价指标的数值越小, 说明融合算法的稳健性越好. 温度数据、 湿度数据和光照数据的比较结果分别列于表2~表4. 由表2和表3可见, 对于温度数据和湿度数据, 本文的融合算法无论是针对全部数据还是局部数据, 方差、 极差、 离散系数这3个评价指标的数值均最小. 由表4可见, 对于光照数据, 本文的融合算法在针对全部数据时, 方差、 极差、 离散系数这3个评价指标的数值均最小; 而对于局部数据, 方差、 极差、 离散系数这3个评价指标的数值均最小. 综合分析可知, 本文的融合算法无论是针对全部数据还是局部数据, 性能均好于其他对比算法.

表2 不同算法对温度数据的融合结果性能对比

表3 不同算法对湿度数据的融合结果性能对比

表4 不同算法对光照数据的融合结果性能对比
综上所述, 本文在分析多种融合方法的基础上, 提出了一种基于可信度的小波神经网络的融合算法, 该算法结合小波和神经网络的优点, 利用传感器的可信度对数据进行融合. 实验结果表明, 本文算法的融合结果在方差、 极差和离散系数等评价指标上均优于其他对比算法, 在数据处理和融合上具有较好的稳定性和可行性.

