Hom-Jordan李超代数的交换扩张
马丽丽, 李 强
(齐齐哈尔大学 理学院, 黑龙江 齐齐哈尔 161006)
1 引言与基本概念
当Hom李代数的扭曲映射为恒等映射时, Hom李代数即为传统的李代数. 目前, 关于Hom李代数的研究已有很多成果[1-2], 且Hom李代数的某些成果已推广到Hom李超代数[3]和Hom李色代数[4]. 文献[5]介绍了Hom李超代数理论, 刻画了Hom李超代数并给出了一个构造定理; 文献[6]得到了Hom李超代数的上同调结构; 文献[3]研究了Hom李超代数的算子和T*-扩张结构; 文献[7-9]讨论了Hom-Jordan李(超)代数的导子、T*-扩张和各种形变. 文献[9]研究了Hom-Jordan李代数的交换扩张, 本文进一步研究Hom-Jordan李超代数交换扩张的性质及其等价交换扩张.
下面先给出Hom-Jordan李超代数的定义和表示, Hom-Jordan李超代数是Hom李代数和李超代数的推广. 符号|·|表示元素·的2-阶化次数.
定义1[8]Hom-Jordan李超代数(L,[·,·]L,α,δ)由超空间L和一个满足
[x,y]=-δ(-1)|x||y|[y,z],δ=±1,
(1)
的二元双线性运算[·,·]L:L×L→L构成.
显然, 当α=I时, Hom-Jordan李超代数即为Jordan李超代数.
定义2[8]1) 若α为态射, 满足α([x,y])=[α(x),α(y)], 则Hom-Jordan李超代数(L,[·,·]L,α,δ)称为保积的;
2) ∀x∈η,y∈L, 若α(η)⊆η并且[x,y]∈η, 则超子空间η⊆L称为Hom-Jordan李超代数(L,[·,·]L,α,δ)的Hom理想.
定义3[8]Hom-Jordan李超代数(L,[·,·]L,α,δ)的表示为向量超空间V上关于A∈pl(V)的线性映射:
ρA:L→pl(V),
使得任意的u,v∈L, 满足
ρA([u,v]L)∘A=ρA(α(u))∘ρA(v)-δ(-1)|u||v|ρA(α(v))∘ρA(u).
(3)

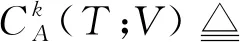
这里
f(x1,…,xi,xi+1,…,xk)=-δ(-1)|xi||xi+1|f(x1,…,xi+1,xi,…,xk).
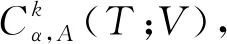
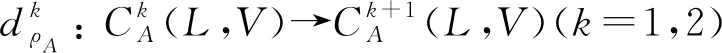
2 主要结果
定义4设(T,[·,·],α,δ)是Hom-Jordan李超代数, (V,ρA,δ)为T-模, 则线性映射ω: ⊗2→V称为2-上圈, 满足:
ω(u0,u1)=-δ(-1)|u0||u1|ω(u1,u0),
定义51) Hom-Jordan李超代数T的理想是超子空间I, 使得[I,T]⊆I;
2) 若满足[T,I]=0, 则理想I称为交换理想.
定理1设ρA是保积Hom-Jordan李超代数(T,[·,·],α,δ)在V上的表示, 这里V是由(T,[·,·],α,δ)全体线性变换构成的超空间. 线性映射ω:T×T→gl(V)满足
ω([x,y],α(z))=-(-1)|z|(|x|+|y|)ω(α(z),[x,y]),
且
ω(x,y)∘α=-(-1)|x||y|α∘ω(x,y).
双线性运算定义为
[x+f,y+g]T⊕V=[x,y]+ω(x,y)-(-1)|x||y|g∘ρA(x)+δf∘ρA(y),
(4)
α′(x+f)=α(x)+f∘α, ∀x,y∈T,f,g∈gl(V).
(5)
则T⊕V关于式(4),(5)定义的运算构成保积Hom-Jordan李超代数当且仅当ω为2-上圈.
证明: 首先验证式(1)成立.
其次验证运算满足式(2).
同理
且
从而

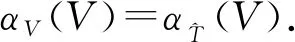
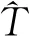



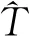
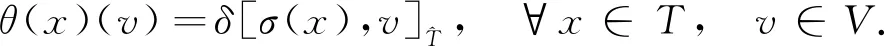
(6)
定理2(V,αV,θ,δ)是(T,α,δ)的表示, 且不依赖于σ的选取, 从而等价交换扩张可给出相同的表示.
p(σ(xi)-σ′(xi))=xi-xi=0⟹σ(xi)-σ′(xi)∈V⟹σ′(xi)=σ(xi)+ui,

表明θ不依赖σ的选取.
其次, 证明(V,αV,θ,δ)是(T,α,δ)的表示. 通过计算可知,
αV(θ(x))(v)=δαV[σ(x),v]=δ[αV(σ(x)),αV(v)]=δ[σ(α(x)),αV(v)]=θ(α(x))αV(v).
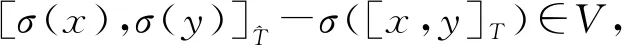
θ([x,y])∘αV(v)=δ[σ[x,y],αV(v)]=δ[[σ(x),σ(y)],αV(v)],
且
从而可知式(3)成立. 于是, 可知(V,αV,θ,δ)是(T,α,δ)的表示.

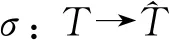
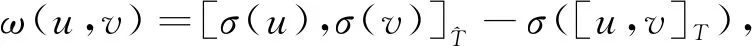
(7)
其中u,v∈T.

证明: 由式(6)和式(7)得,

