工业机器人动力学参数辨识与自适应控制方法研究

徐建明，赵 帅

(浙江工业大学 信息工程学院，浙江 杭州 310023)

工业机器人广泛应用于工业生产过程中的搬运、装配、涂装等方面，并且正向着高速、高精度、高智能化的方向发展，加之产业需求的不断扩大与提升，诸如新型的激光焊接、激光切割、多机器人协作等任务对机器人的控制精度提出了更高要求[1-2]。设计基于机器人动力学模型的控制器是实现高速高精度运动控制的有效途径[3]，但该类控制器的设计需要已知机器人的动力学参数。一般情况下，机器人的动力学参数难以直接测量，需采用特定的辨识实验获得[4]。Atkeson等[5]选择关节空间的五次多项式作为激励轨迹，采用最小二乘法作为参数估计的方法。Swevers等[6]首次提出了采用基于傅里叶级数的激励轨迹进行辨识实验，该方法产生较大影响，在随后的辨识研究中，基本均采用傅里叶级数作为激励轨迹[7]。傅里叶级数是指由不同幅值和周期的三角函数构成的非线性函数，该函数具有连续的多阶导数，其二阶导数具有较大幅值，能充分激发系统的动态特性；并且通过合理设置参数，能保证函数起始和结束时刻具有相同值，便于机器人重复执行激励轨迹。但传统傅里叶级数形式的激励轨迹无法保证各关节的角速度和角加速度在轨迹的起始和停止时刻为零，导致机器人在执行激励轨迹时存在抖动。文献[8]在此基础上提出了一种基于改进的傅里叶级数的辨识方法，该方法考虑速度、加速度边界条件，保证激励轨迹起始阶段的稳定性，提高了辨识精度。目前，确定激励轨迹参数有两种应用较多的方法，一种是基于回归矩阵的条件数最小化方法[9]；另一种是基于对数行列式的优化方法[10]。参数估计的方法也有很多，其中应用较多的两种方法为最小二乘法[11]和最大似然估计法[8]。其他的方法包括扩展卡尔曼滤波法[12]，加权最小二乘法[12]，非线性最小二乘法[13]等。在机器人控制方面，Slotine等做了大量深入的研究，提出了直接自适应、间接自适应、复合自适应等控制算法[14-17]；针对机器人工作环境限制、负载变化等问题，提出将自适应理论结合阻抗控制，并证明了控制系统的稳定性[18]；焦晓红等[19]将自适应结合鲁棒控制，针对误差扰动上界确定和不确定两种情况提出控制律，并通过仿真证明了控制算法的可行性。文献[20]提出了自适应神经网络控制算法。利用径向基神经网络来调整滑模控制增益，消除滑模控制输入抖动并优化系统性能。

笔者以ZCR07S六自由度工业机器人为实验研究对象，基于Codesys平台完成机器人动力学参数辨识实验与自适应控制实验。辨识出一组动力学参数并实现了自适应控制算法。

1 机器人动力学模型与参数辨识

1.1 机器人动力学特性

n连杆刚性机器人动力学方程可由二阶非线性微分方程[21]描述为

(1)

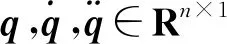
机器人系统的动力学结构特性如下：

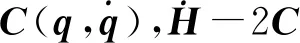
(2)

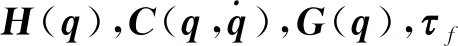
(3)

式(3)中Y的有些列恒为零，有些列间存在常值线性关系，所以不是所有惯性参数都对力矩有影响，通过线性关系重组标准惯性参数[11,22]或数值解析方法[23]获得可辨识的最小惯性参数集amin。式(3)可重写为

(4)

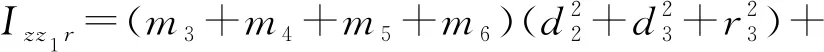
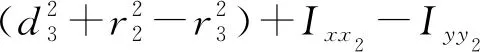
Ixz2r=Ixz2-d3(m3+m4+m5+m6+mz3)r3

mx2r=d3(m3+m4+m5+m6)+mx2

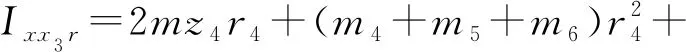
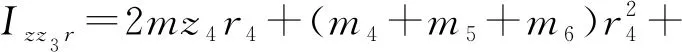
my3r=my3-mz4-(m4+m5+m6)r4

Ixx4r=Ixx4-Iyy4+Iyy5

Izz4r=Iyy5+Izz4

my4r=Imy4+Imz5

Ixx5r=Ixx5-Iyy5+Iyy6

Izz5r=Iyy6+Izz5

my5r=Imy5-Imz6

Ixx6r=Ixx6-Iyy6

表1 最小惯性参数Table 1 Minimum inertial parameters

1.2 动力学参数辨识原理及实验

为实现基于动力学模型的控制，需要对结构已知的模型参数进行辨识，获取机器人的一组最小惯性参数值，即式(4)中的amin。机器人的参数辨识是一个复杂的系统工程，包括运动学与动力学建模、激励轨迹的选取、实验设计、数据采集与处理、参数估计、模型验证等环节，其流程图如图1所示。

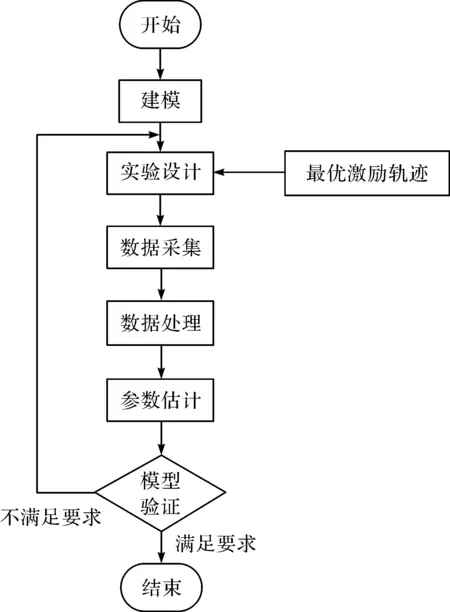
图1 辨识实验流程图Fig.1 Flow chart of identification experiment

ZCR07S机器人6 个关节均为旋转关节，本体如图2所示，运动学模型的建立采用文献[11]中的方法，连杆坐标系如图3所示，MDH参数如表2所示。

图2 实验机器人本体Fig.2 Experimental robot body

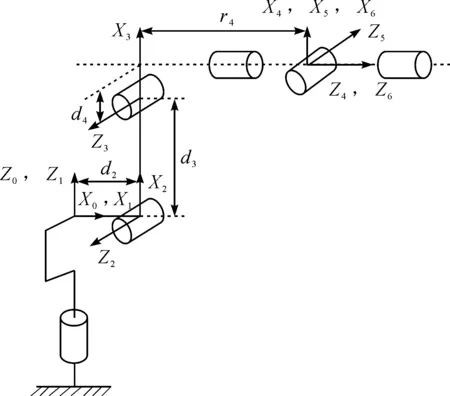
图3 连杆坐标系Fig.3 Connecting rod coordinate system

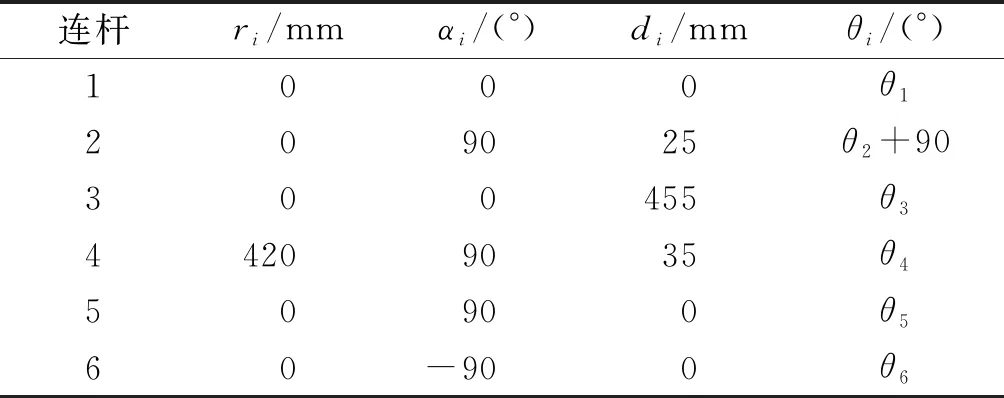
表2 MDH参数Table 2 MDH parameters

动力学模型由SYMORO+[24]软件推导，以自定义符号表达式形式在robot-name.dyn文件中给出，由于篇幅限制，文中不再给出。

各关节激励轨迹为N次谐波的正弦和余弦函数有限项和，激励轨迹关节角位置表达式为

(5)

关节角速度、角加速度分别为一阶、二阶导数。实验中：基频为0.1 Hz；周期为10 s；N为5；qi0为位置偏移量；al，bl确定了三角函数的幅值。

确定激励轨迹参数al,bl,qi0的问题可描述为非线性约束优化问题：

优化目标为

q*(t)=argmin(J)

(6)

约束条件为

(7)

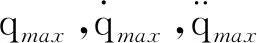
表3 各关节位置、速度限位Table 3 Position and speed limitation of joints

式(7)中后面的3 个约束条件保证了激励轨迹起始和终止位置、速度、加速度为零。根据Hadamard不等式，正定矩阵的行列式小于等于其对角项的乘积，可计算det(YTY)上界，可最小化矩阵条件数。目标函数J[25]为

式中Y为m×n的回归矩阵，Yij为矩阵Y的第i行第j列元素。通过MatlabFunction函数计算目标函数参数，将目标函数与式(7)中的约束条件代入到Matlab fmincon函数计算激励轨迹参数。激励轨迹如图4所示。

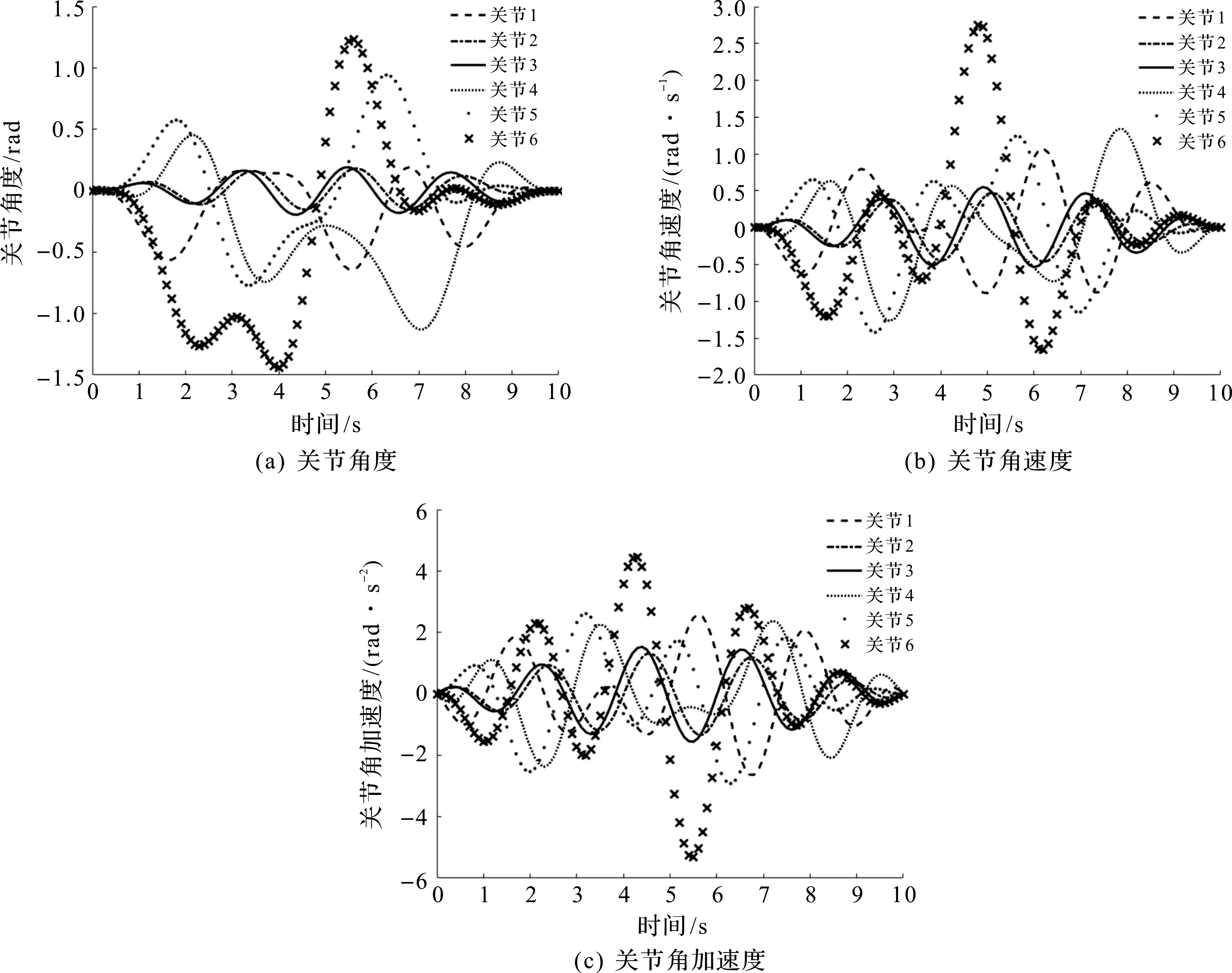
图4 激励轨迹Fig.4 Excitation trajectory

辨识实验设计与数据采集通过Codesys平台完成，同时采集关节角位置、速度和力矩，采样频率为250 Hz。由Codesys采集到的力矩经过如下转换关系换算为机械臂端力矩：机械臂端力矩=采集的力矩相对值×电机额定力矩×减速器减速比/1 000。实验所用电机额定力矩和减速器减速比如表4所示。

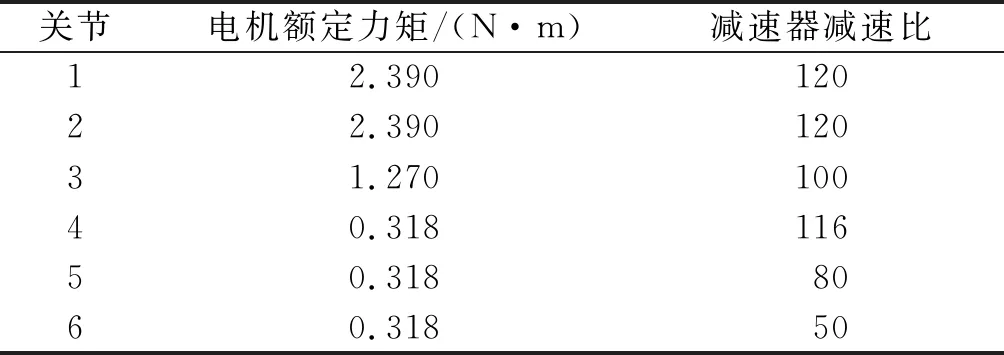
表4 电机额定力矩和减速器减速比

实验中采集的关节位置轨迹光滑，无需滤波处理，关节速度、加速度通过中心差分算法计算得到，并通过Matlab smooth函数对关节加速度、力矩进行平滑处理。

最小惯性参数值的估计采用标准最小二乘法，去除掉一些相对标准偏差较大(RSD>30%)的惯性参数后，得到29 个描述6 个关节机器人动力学模型的最小惯性参数，如表5所示。

表5 最小惯性参数值Table 5 Minimum inertial parameter values

通过比较实测力矩与由辨识模型所估计的力矩的均方根误差来判断所辨识的模型是否符合精确度要求。图5为重新生成的一组验证轨迹。

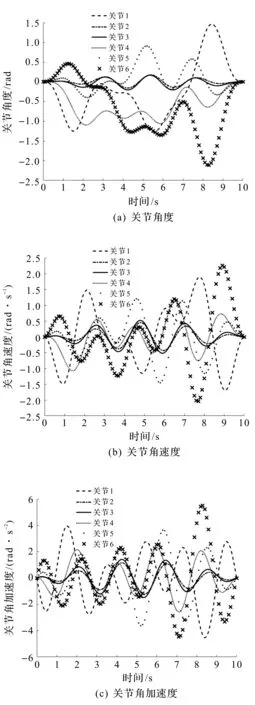
图5 验证轨迹Fig.5 Verification trajectory

图6，7分别代表激励轨迹和验证轨迹下的实测力矩与估计力矩。

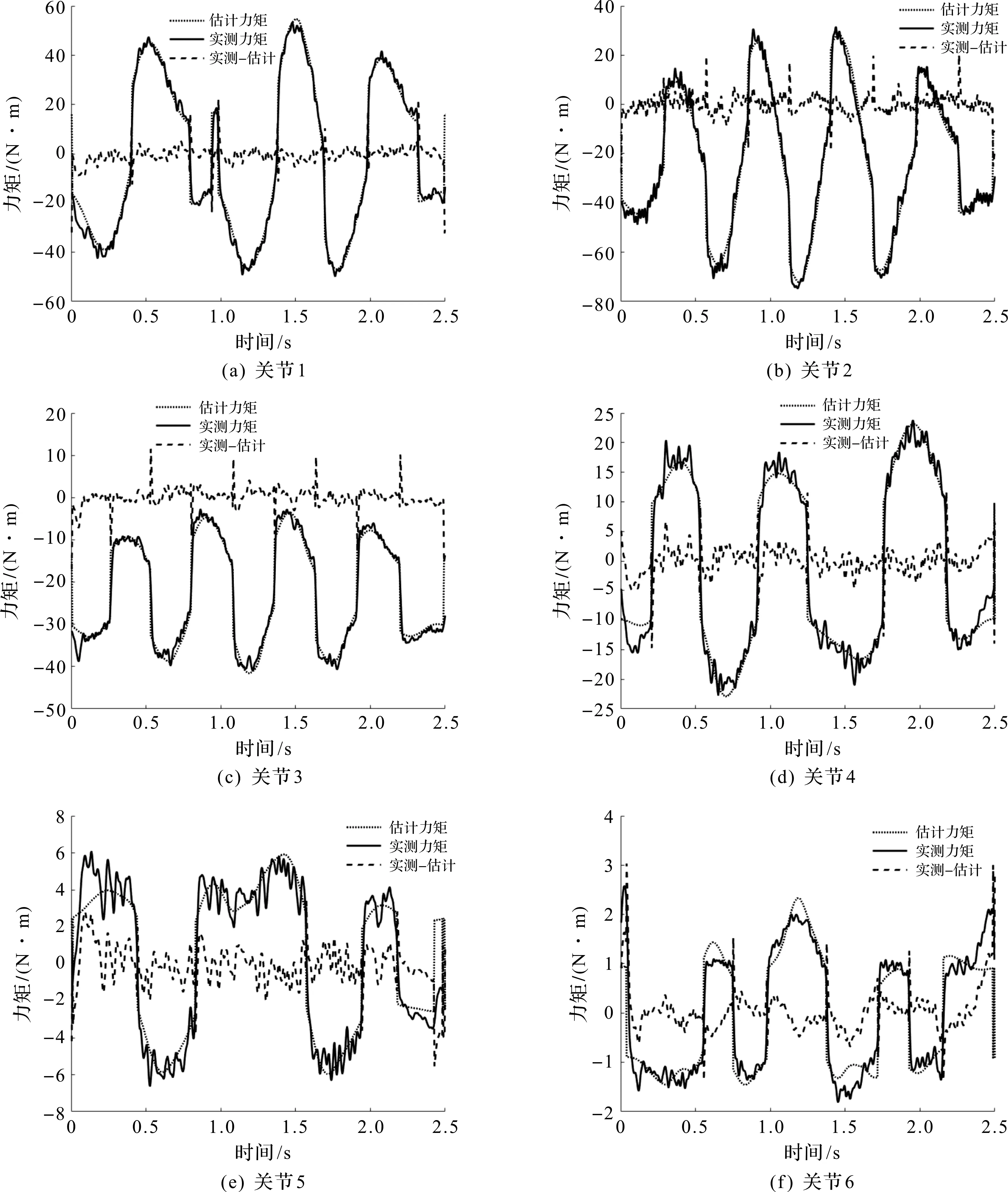
图6 6 个关节激励轨迹下实测力矩与估计力矩图Fig.6 Measured and estimated torque diagrams under 6 joint excitation trajectories

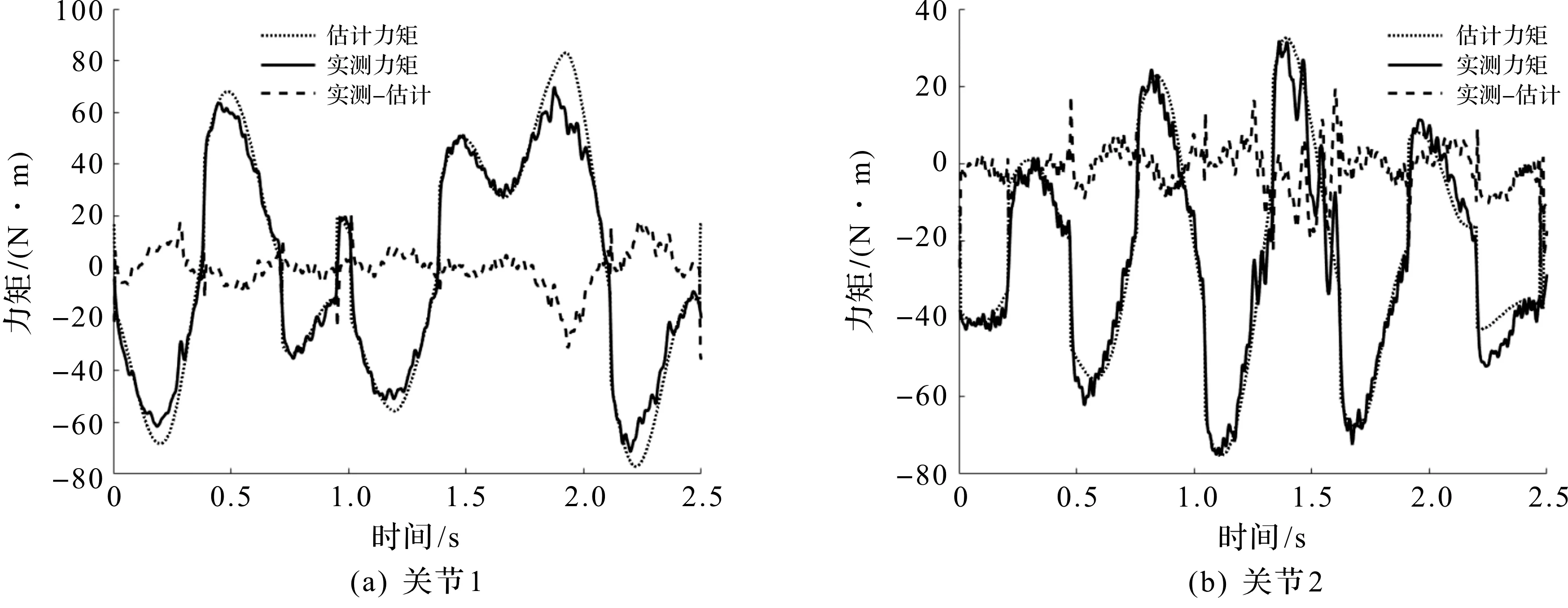
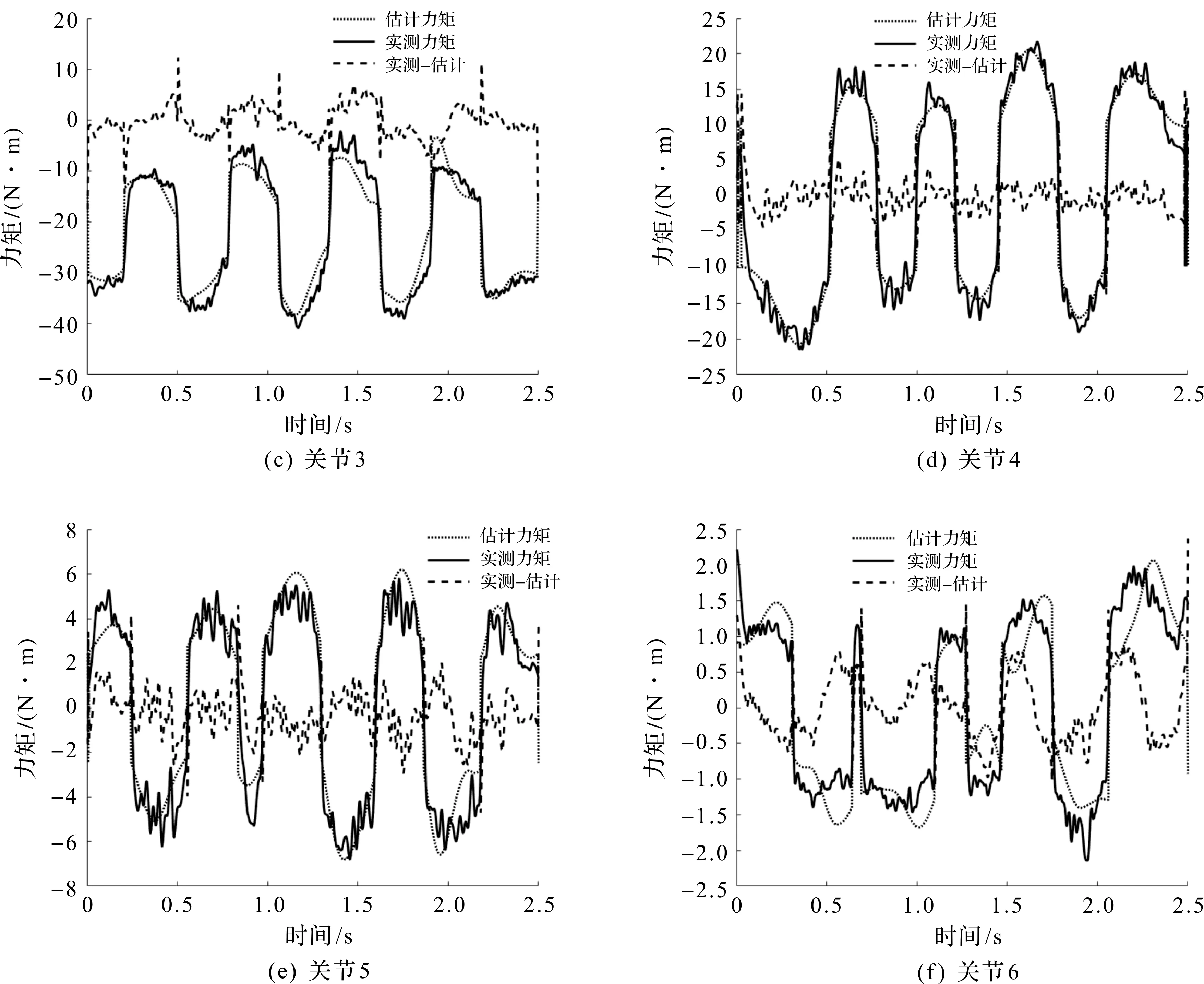
图7 6 个关节验证轨迹下实测力矩与估计力矩图Fig.7 Measured and estimated torque diagrams under 6 joint verification trajectories

表6为激励轨迹和验证轨迹下的实测力矩与估计力矩的均方根误差，误差值较小，辨识的模型可用。

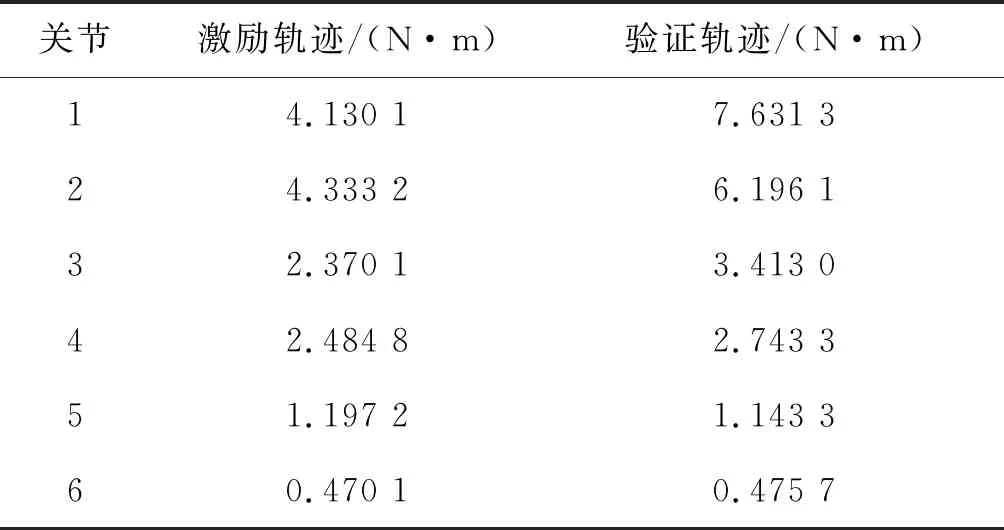
表6 均方根误差Table 6 RMS error

2 自适应控制算法实验

2.1 自适应控制器的实现

选择控制律和自适应律[14]为

(8)

(9)

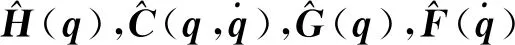
(10)

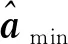
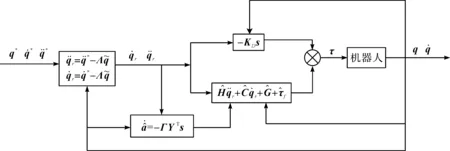
图8 自适应控制器结构图Fig.8 Structure diagram of adaptive controller

2.2 实验装置

研究中使用的六轴工业机器人控制系统采用一主多从的控制模式，主站采用ARM+Linux控制方案，从站采用带EtherCAT接口的高创CDHD系列伺服驱动，主站与从站、从站与从站之间的通讯采用工业以太网EtherCAT技术，软件平台以Codesys作为开发环境，以ST和CFC作为主要编程语言实现机器人动力学控制，机器人控制系统结构如图9所示。

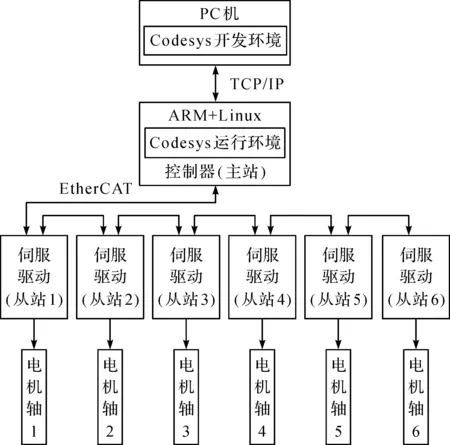
图9 控制系统结构Fig.9 Control system architecture

2.3 实验结果

实验的期望轨迹为

程序运行采样周期为4 ms，自适应增益均为1，在实际的调节过程中，根据系统的稳定性与跟踪性能之间的权衡，确定KD=diag[400,350,130,22,9,2]，Λ=diag[10,10,10,30,30,25](KP=ΛKD)。实验结果如图10所示，图10中曲线由上至下分别代表期望位置y1,实际位置y2,期望速度y3,实际速度y4,位置误差y5,速度误差y6。跟踪过程中，关节1至关节6最大位置误差分别为-0.06°，0.22°，0.34°，-0.29°，0.45°，0.85°。关节1至关节6位置定位误差分别为-0.06°，0.02°，0.04°，-0.11°，-0.11°，0.09°。

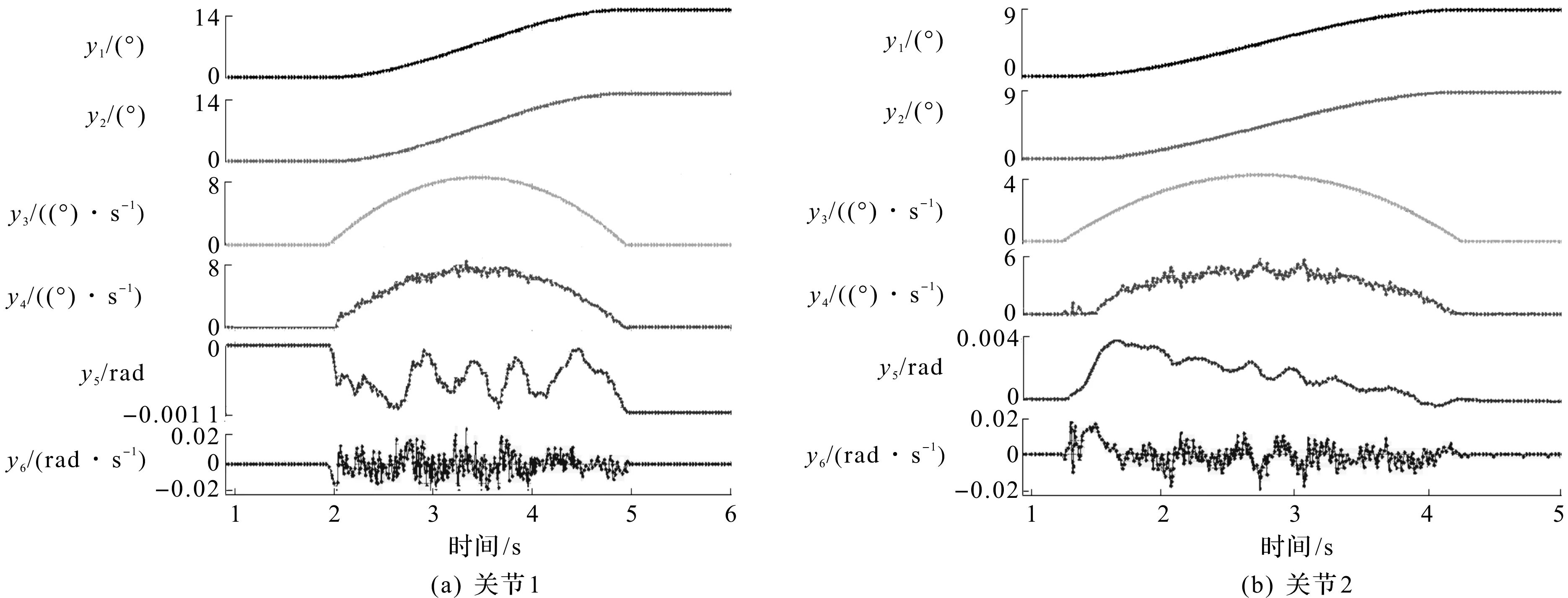
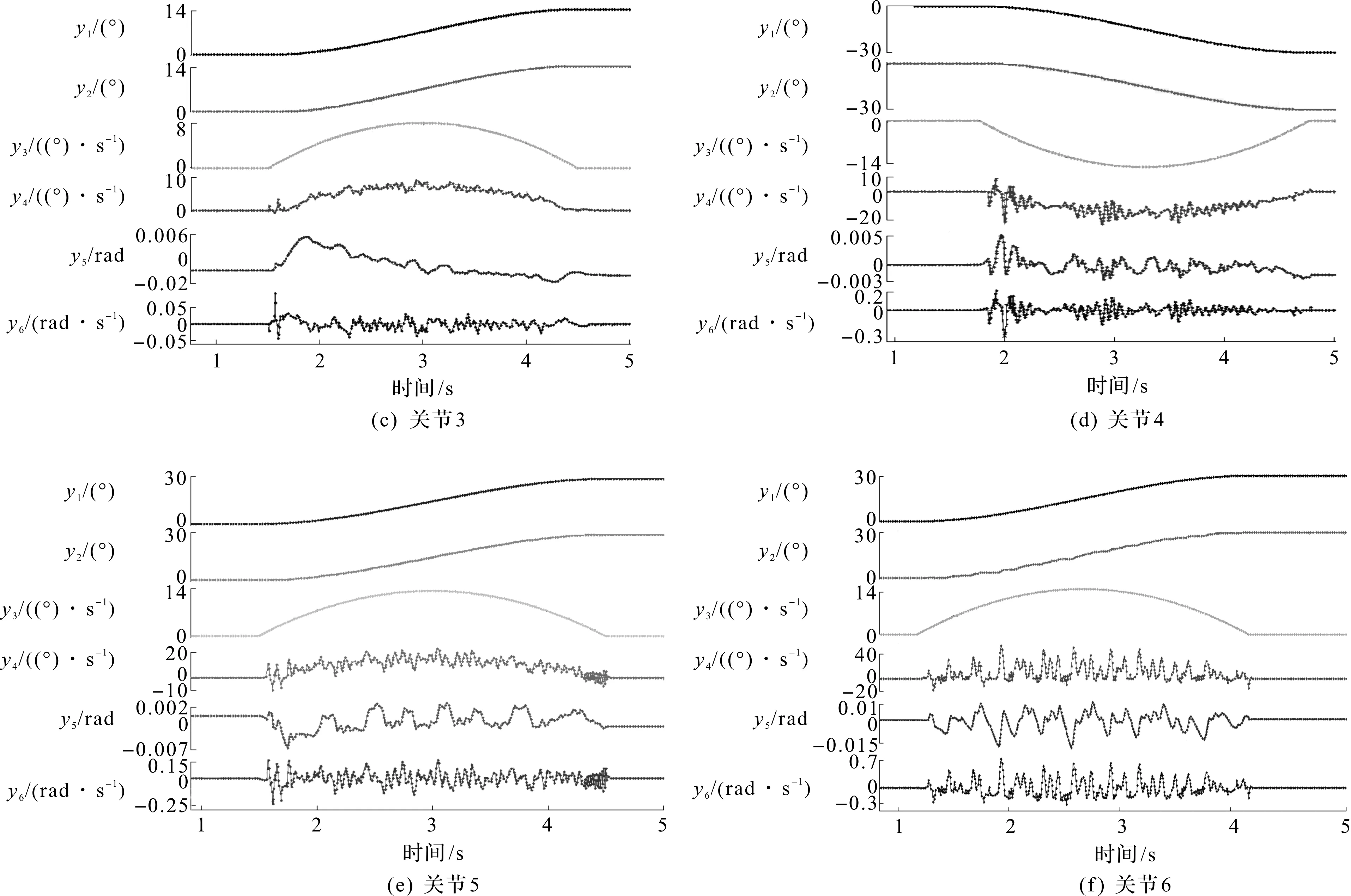
图10 关节1至关节6的跟踪结果图Fig.10 Tracking results of joint 1 to joint 6

3 结 论

采用一种计算效率高的优化准则设计辨识实验的激励轨迹，通过Codesys平台完成辨识实验，去掉相对标准偏差较大的惯性参数后，得到29 个描述机器人动力学特性的最小惯性参数，并通过验证轨迹验证了辨识参数的精确性；接着基于所辨识的最小惯性参数和机器人动力学模型，将一种自适应控制算法应用于六自由度工业机器人轨迹跟踪控制，通过实验验证了所研究方法的有效性。主要体现为应用创新：第一个创新点是辨识出了ZCR07S工业机器人动力学参数；第二个创新点是将自适应控制算法应用于ZCR07S工业机器人，并取得了良好的控制效果。