结合先验知识和稀疏表示误差的感知矩阵设计

何熊熊，姜倩茹，李 胜，常丽萍，张 霓

(浙江工业大学 信息工程学院，浙江 杭州 310023)

大数据[1-2]时代对如何实现节约数据存储空间和提高数据传输效率提出了巨大的挑战。压缩感知技术[3-8]能够将可被稀疏表示[9-10]的数据通过一个感知矩阵[11-13]进行压缩，并通过求解欠定方程从低维观测值中成功重构原始数据[14-16]。该技术现已被广泛应用于医学图像处理[17]、深度学习[18]、人脸识别[19]以及无线传感网络[20]等领域。在传统的感知矩阵设计方法[21-22]中，通常将字典的Gram矩阵逼近单位矩阵，如Duarte-Carvajalino等[21]在2009年提出将等效字典Gram矩阵近似逼近单位矩阵，但是此算法的物理意义不明确。Li等[22]在2013年提出将Gram矩阵直接逼近单位矩阵，但是没有考虑稀疏表示误差对系统的影响，使得该算法不适用于存在不可忽略的稀疏表示误差的图片数据中。Li等[23]在2015年又提出在感知矩阵设计中考虑稀疏表示误差对系统的影响，增加了系统的鲁棒性，但是稀疏表示误差中巨大的数据量会给系统带来过大的运算负担。因此Hong等[24]在2018年提出了通过对感知矩阵映射下的稀疏表示误差进行估计的感知矩阵设计方法，与文献[23]提出的算法具有相似的恢复效果，但大大降低了其计算复杂度。Li等[25]在2017年提出将等效字典Gram矩阵逼近单位矩阵的代价函数中，引入根据稀疏系数幅值产生的先验知识设计感知矩阵，虽然在数据恢复的精确度上有所提高，但该设计不适用于图片恢复。因为图片[26]列与列之间的稀疏系数的非零幅值千差万别，采用此方法则需要不停地设计感知矩阵，增加了计算负担。

为了提高图片数据恢复的精确度并降低计算负担，笔者结合从图片中提取先验知识和对感知矩阵映射下的稀疏表示误差进行估计这两方面来设计感知矩阵。首先将图片样本在字典下进行稀疏表示获得稀疏矩阵，然后通过统计稀疏矩阵行的非零元素分布率来提取先验知识，该先验知识反映的是字典(或者等效字典)原子被使用的程度。利用该先验知识设置一个对角权重矩阵来构造感知矩阵设计模型，在此权重矩阵作用下使得等效字典Gram矩阵无限接近单位矩阵来减小等效字典的平均互相关系数[11]，尤其是那些被频繁使用的等效字典原子的平均互相关系数。与此同时对感知矩阵映射下的稀疏表示误差进行估计并用合适参数配置下的感知矩阵的佛罗贝尼乌斯(Frobenius)范数进行替代。可总结为：1) 从大量图片样本的统计信息中提取先验知识，利用先验知识构造一个权重矩阵用于感知矩阵设计；2) 在感知矩阵设计模型中考虑稀疏表示误差对数据恢复的影响，对感知矩阵映射下的稀疏表示误差进行估计并用合适参数配置下的感知矩阵的佛罗贝尼乌斯范数进行替代来减小计算复杂度[27]；3) 该感知矩阵设计算法分别用于合成数据和实际场景图片可获得良好的恢复效果。

1 问题描述

传统的感知矩阵设计模型可表示为

(1)

式中：‖·‖F为矩阵的佛罗贝尼乌斯(Frobenius)范数；IK为K维单位矩阵；G为等效字典的Gram矩阵，被定义为G=DTD=ΨTΦTΦΨ，其中Φ∈RM×N为感知矩阵，Ψ∈RN×K为字典，D∈RM×K为等效字典。分析式(1)可知：

(2)

式中：G(i,j)表示矩阵G的第i行，第j列的元素。要使得等价函数最小，可将等效字典进行归一化使得Gram矩阵对角元素为1，还需将Gram矩阵的非对角元素值逼近单位矩阵的零元素。Gram矩阵非对角元素表示等效字典对应原子之间的互相关性[11]，因此传统的感知矩阵设计是基于减小等效原子之间的互相关性而实现的。

在图片恢复的真实应用场景中，需要利用大量图片样本对字典进行训练[28-29]使得图片能够被更好地稀疏表示。字典训练模型可表示为

(3)

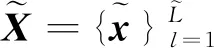
(4)

式中向量p为从图片样本中获取的关于稀疏矩阵行的非零元素分布率的先验知识。在感知矩阵设计模型中，根据字典原子被使用频率的不同，加入一个关于先验知识的权重矩阵，着重减小那些使用频率较高的原子之间的互相关性，使得数据恢复精确度被进一步的提高。关于先验知识的权重矩阵ΣW可表示为

ΣW(k,k)=τ+(1-τ)p(k)

(5)

可得式(5)的感知矩阵设计模型被优化为

(6)

由于图片中存在不可忽略的稀疏表示误差(SRE)[23]，可表示为

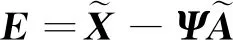
(7)

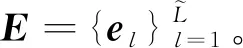
(8)

通过对代价函数式进行求解来设计感知矩阵，在该模型中同时考虑概率型先验知识和稀疏表示误差，求得的感知矩阵为解析解。

2 基于先验知识并考虑稀疏表示误差的感知矩阵设计

结合先验知识和稀疏表示误差对系统的影响，感知矩阵设计的代价函数可表示为

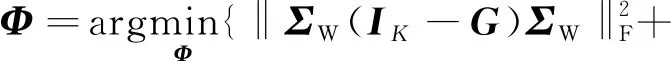
(9)

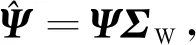
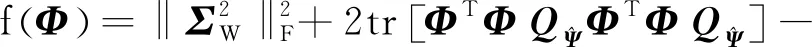
(10)

式中tr[·]表示矩阵求迹，其中

(11)

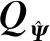
(12)

那么，式(9)可化简为

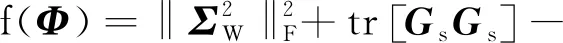
(13)

其中

(14)

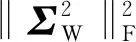
(15)

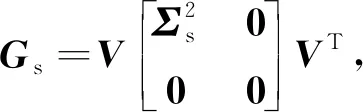
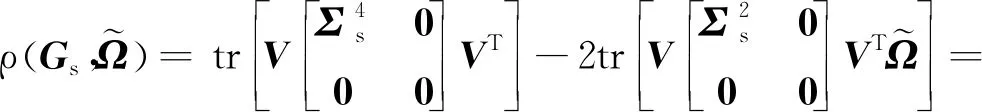
(16)

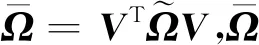
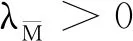
1) 当λM>0时，观察可得：

(17)

根据文献[30]附录B中的引理1可知：

(18)

(19)

(20)

(21)

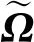
总结以上3 种情况，感知矩阵解的形式可表示为

(22)

式中：U为任意的正交矩阵；Σs,V11,V22分别根据以上3 种情况而设计。

3 仿真与实验结果分析

针对合成数据和真实应用场景图片对所提出的感知矩阵算法与现有算法进行仿真对比来验证算法的有效性。

3.1 数据恢复的评价指标

根据上述合成数据中非零元素的概率分布，利用平均二元熵(Average binary entropy, ABE)[31]，来测试稀疏系数信息的不确定性，以概率为p(k)的伯努利分布的熵定义为

(23)

式中H(p(k))=-p(k)logp(k)-(1-p(k))·log(1-p(k))是二元熵函数。稀疏系数非零元素概率分布越不均匀，平均二元熵就越小。

对于数据恢复的性能指标，将采用平方根误差(Mean square error, MSE)[30]，定义为

(24)

还对恢复的稀疏系数位置的准确率进行对比，将此性能指标定义为

(25)

针对图片数据的恢复，采用峰值信噪比(Peak signal-to-noise ratio，PSNR)[30]作为性能指标，其计算式为

(26)

式中每个像素点的r=8 bits。图片的均方根误差可写为

(27)

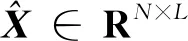
3.2 合成数据对比仿真

3.2.1 合成数据的产生

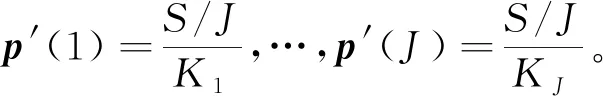
3.2.2 合成数据对比结果与分析

在此对比实验中，感知矩阵大小为M×200，字典大小为200×240。稀疏系数的维度为K=240，稀疏度为S。此向量被分成J=4段，每段元素个数为K1=160,K2=50,K3=20,K4=10。稀疏系数中的非零元素服从N(0,1)的高斯分布。测试数据x是含有一定稀疏表示误差的可压缩数据，其信噪比可表示为SNR，即x=Ψα+eSNR。此实验重复L=1 000 次。

笔者提出的感知矩阵设计方法为SMW-HT算法，对比算法分别是：感知矩阵为Φ0的SMRAN算法、SMDCS算法[21]、SMLG算法[23]以及SMHT算法[24]。采用的恢复算法为正交匹配追踪算法(OMP)[15]。

该实验首先对感知矩阵设计的代价函数的参数τ,δ进行选取，τ的取值从0到1，取值间隔为0.1。δ的取值从0到2，取值间隔为0.1。经过实验表明：当τ=0.6,δ=0.1时，测试数据的MSE最小。在以下对比实验中，SMW-HT算法的参数取值为τ=0.6,δ=0.1，SMHT算法的参数取值[24]为δ=0.1，SMLG算法的参数取值[23]为δ=1。

实验1表1分别列出了5 种对比算法的Gram矩阵与单位矩阵的接近程度、感知矩阵映射下的稀疏表示误差、互相关系数以及平均互相关系数[11]。该实验中感知矩阵维数M=50，稀疏度S=12，表示误差信噪比为SNR=20 dB。从表1可以看出：笔者提出的SMW-HT算法在以上4 种性能指标中均与同类算法SMLG，SMHT表现相似，下面实验将对数据的恢复效果作进一步的验证。

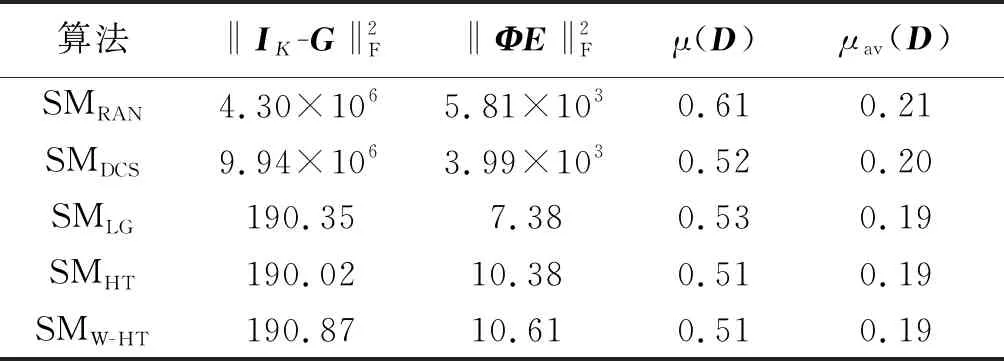
表1 5 种感知矩阵设计算法的性能评估Table 1 Performance evaluated with five sensing matrices

实验2将5 种观测矩阵设计算法在测试数据包含不同信噪比的稀疏表示误差下进行对比来验证合成数据的恢复效果，图1显示的是SNR从15 dB到40 dB变化下的均方根误差(MSE)，图2显示的是稀疏系数非零元素位置恢复准确率。此实验的参数为M=50,S=12。

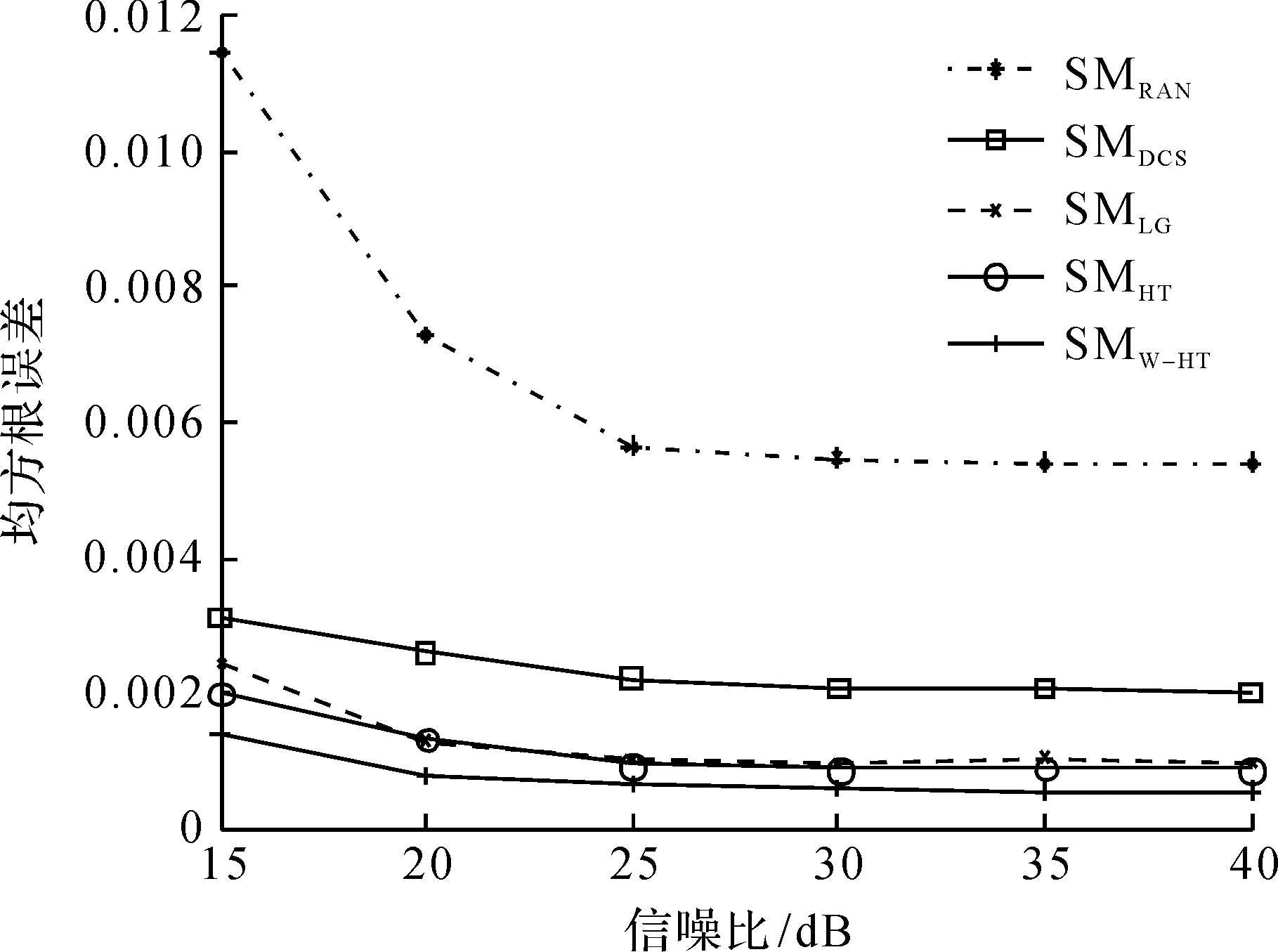
图1 不同信噪比下5 种感知矩阵设计算法的均方根误差Fig.1 The MSE versus different level SNR for sensing matrices

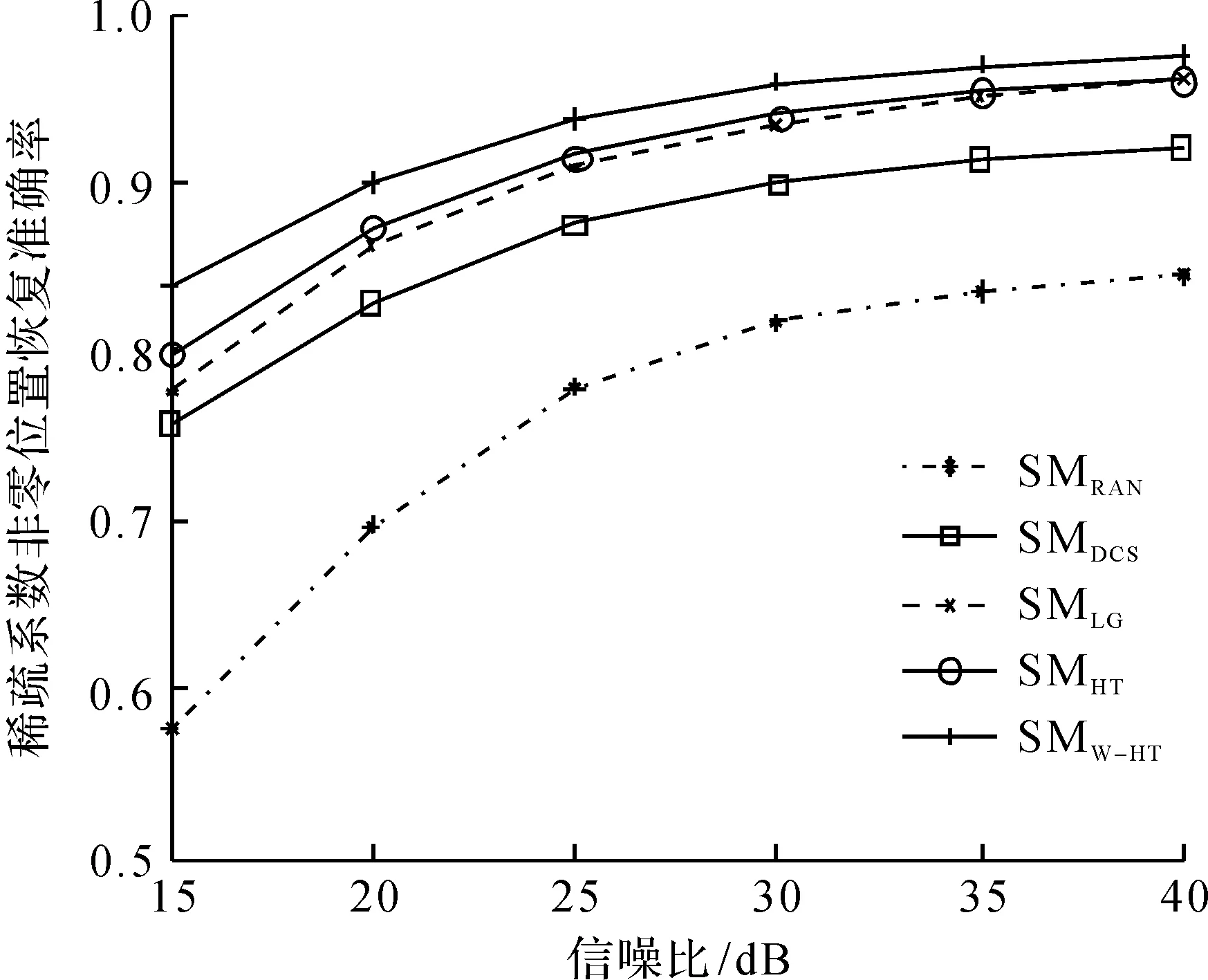
图2 不同信噪比下5 种感知矩阵设计算法的稀疏系数非零元素位置恢复准确率Fig.2 The proportion of successful recovery coefficients five versus different level SNR for five sensing matrices

实验3将5 种观测矩阵设计算法在不同稀疏度下进行对比来验证合成数据的恢复效果，图3显示的是稀疏度从8到24下的均方根误差(MSE)，图4显示的是稀疏系数非零元素位置恢复准确率。此实验的参数为M=50,SNR=20 dB。

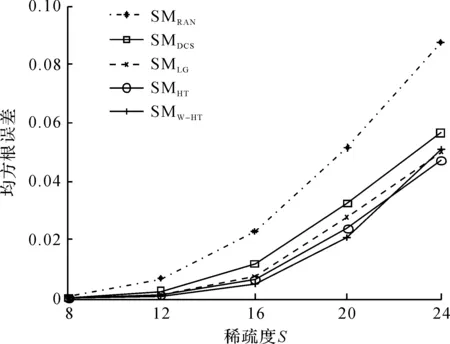
图3 不同稀疏度下5 种感知矩阵设计算法的均方根误差Fig.3 The MSE versus different sparsity for five sensing matrices

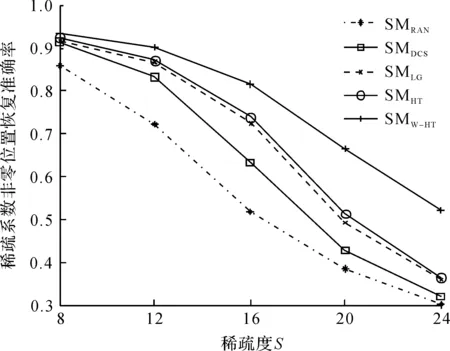
图4 不同稀疏度下5 种感知矩阵设计算法的稀疏系数非零元素位置恢复准确率Fig.4 The proportion of successful recovery coefficients versus different sparsity for five sensing matrices

实验4将5 种观测矩阵设计算法在不同压缩维度下进行对比来验证合成数据的恢复效果，图5显示的是观测矩阵维度从35到65下的均方根误差(MSE)，图6显示的是稀疏系数非零元素位置恢复准确率。此实验的参数为S=12,SNR=20 dB。

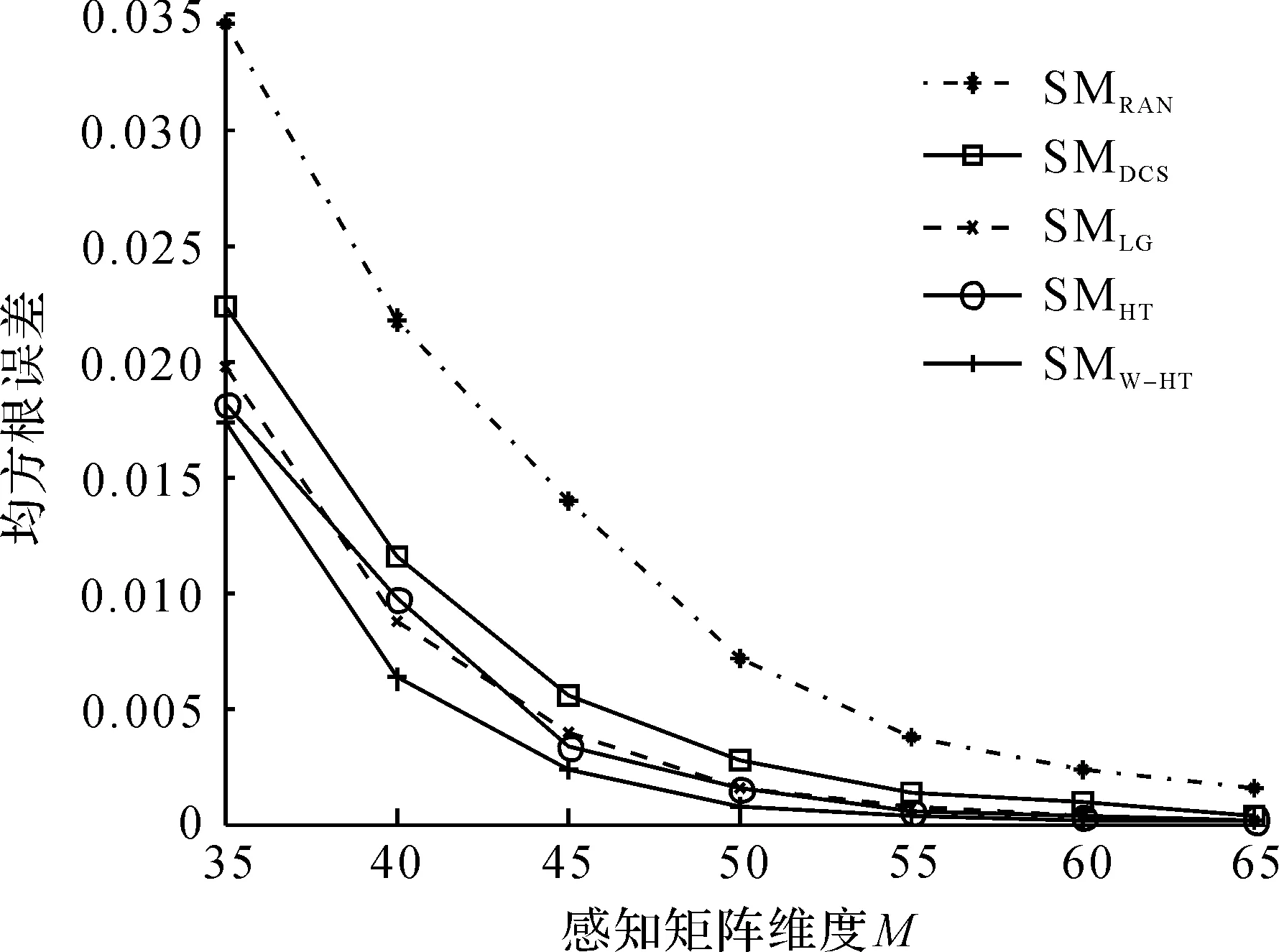
图5 感知矩阵不同维度下5 种感知矩阵设计算法的均方根误差Fig.5 The MSE versus different dimension of sensing matrix for five sensing matrices

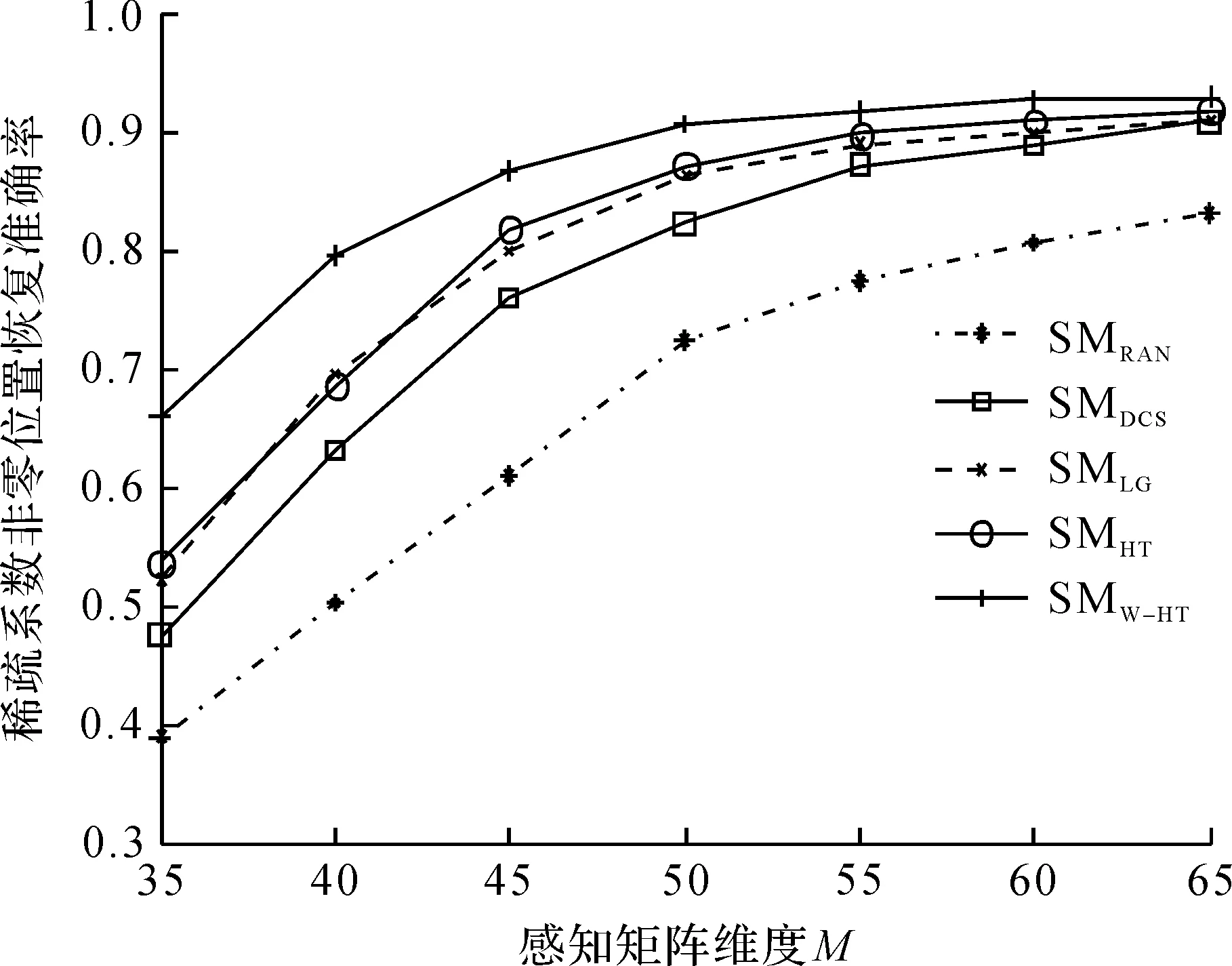
图6 感知矩阵不同维度下5 种感知矩阵设计算法的稀疏系数非零元素位置恢复准确率Fig.6 The proportion of successful recovery coefficients versus different dimension of sensing matrix for five sensing matrices

从图1～6可以看出：笔者提出的SMW-HT感知矩阵设计方法在均方根误差和稀疏系数非零元素位置恢复准确率这两方面的性能指标上较其他4 种感知矩阵设计方法具有最好的性能。此外，当测试数据的表示误差、稀疏度、数据压缩比(即感知矩阵维度)等这3 个参数分别变化时，笔者提出的SMW-HT感知矩阵设计方法始终保持性能最好。分析文献[24]可得：在数据量不大的情况下(L=1 000)，SMLG算法，SMHT算法性能相似，这在仿真结果中也得到了验证。

实验5为了验证数据所包含信息的不确定性而产生不同先验概率对信号恢复精确度的影响，将稀疏系数进行不同的分段，分段方案如表2所示。

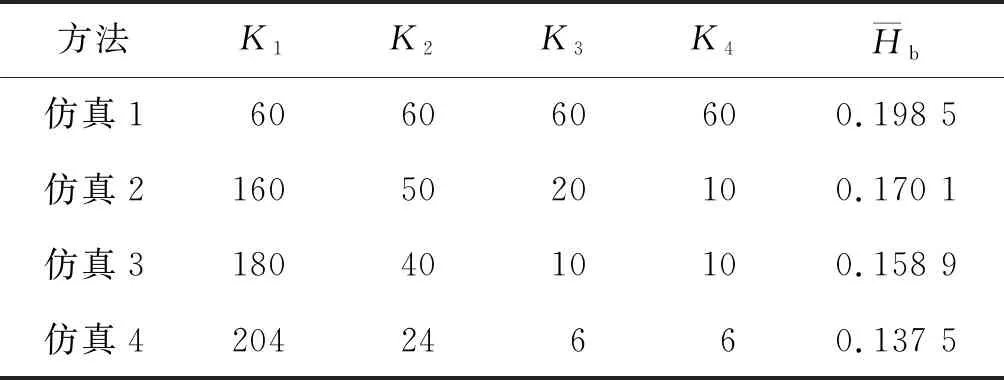
表2 稀疏系数的不同分段中每段所含元素个数Table 2 The length of every group in each simulation

图7，8分别展示了不同先验知识作用下的SMW-HT感知矩阵将测试数据进行压缩后通过OMP算法恢复的效果。根据平均二元熵(ABE)的定义可知：平均二元熵越小，则概率分布越不均匀，也就是所含先验知识的信息量越大。从仿真结果看：先验知识所含的信息量越大，对感知矩阵的设计帮助越大。

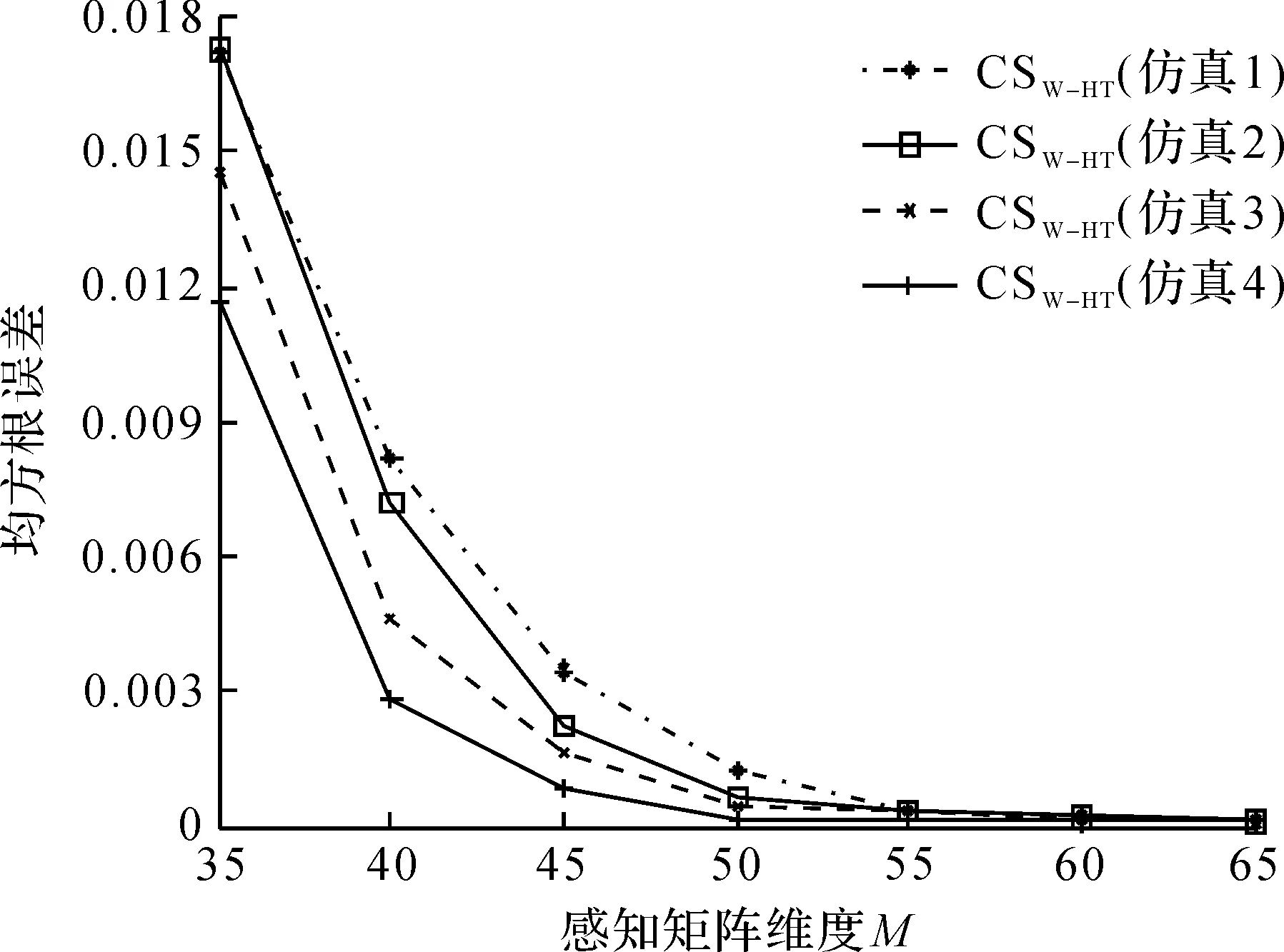
图7 感知矩阵不同维度下对于不同先验知识作用下的感知矩阵设计算法的均方根误差Fig.7 The MSE versus different dimension of sensing different probability distribution of non-zero sparse coefficient

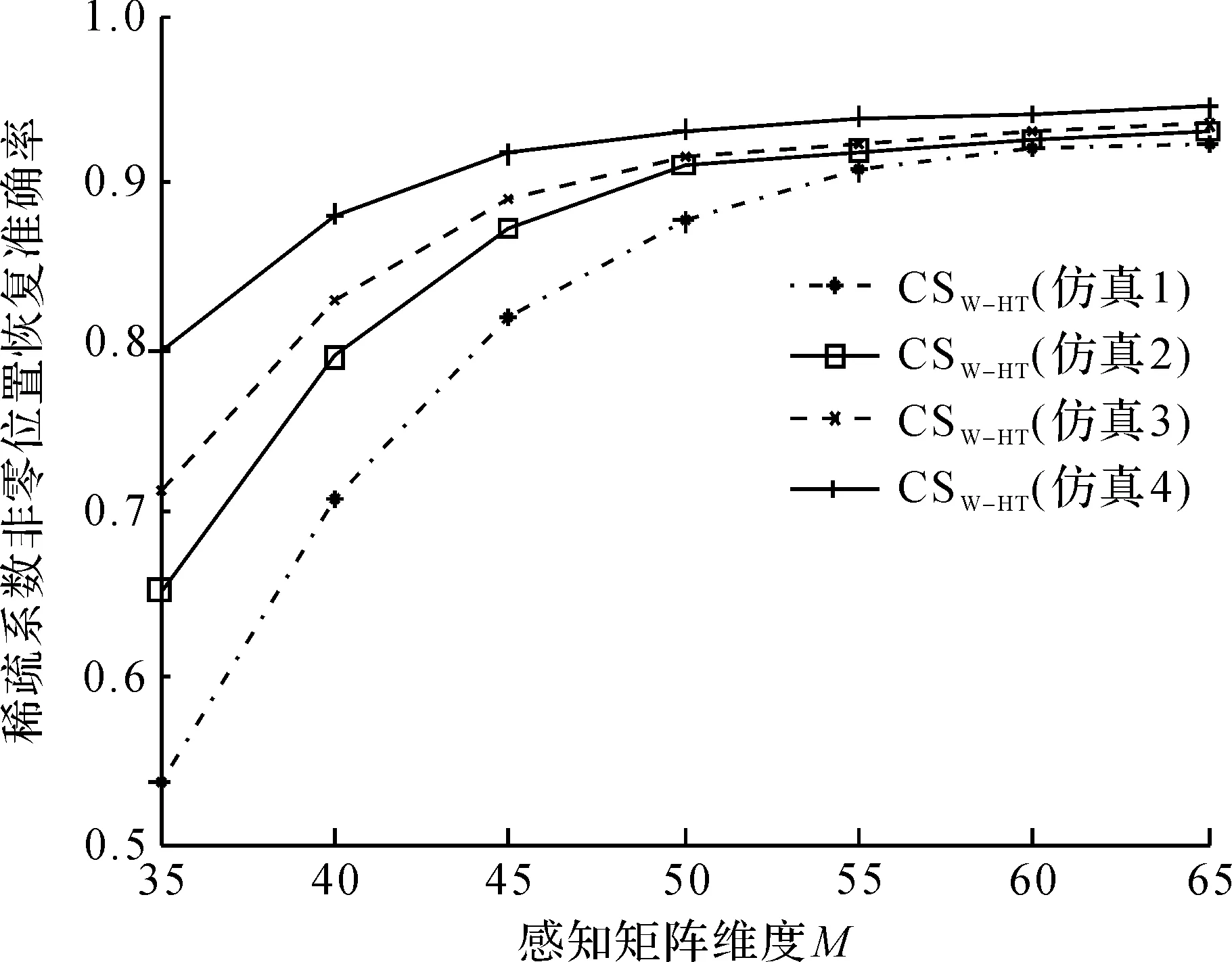
图8 感知矩阵不同维度下对于不同先验知识作用下的感知矩阵设计算法的稀疏系数非零元素位置恢复准确率Fig.8 The proportion of successful recovery coefficients matrix for versus different dimension of sensing matrix for element in different probability distribution of non-zero element in sparse coefficient

3.3 实际应用场景图片对比实验

将笔者提出的算法和对比算法用于实际应用场景图片来验证图片的恢复效果。与合成数据中的对比算法相同，采用感知矩阵为Φ0的SMRAN算法、SMDCS算法[21]、SMLG算法[23]和SMHT算法[24]与新提出的SMW-HT算法进行对比。从LabelMe图片训练库[32]中随机选取400 张图片，又从每张图片中随机选择15 个8×8的块，排列成64×6 000的列作为训练样本。字典选用64×100的离散余弦变换(DCT)字典为起点，利用这些样本采用KSVD算法[29]对字典进行训练。该实验采用的恢复算法为OMP算法[15]。将峰值信噪比(PSNR)作为评价图像恢复效果的性能指标。

实验6计算图片恢复的峰值信噪比验证感知矩阵设计的性能。表3对12 张自然图片进行恢复，并计算它们的峰值信噪比。其中，感知矩阵维度为M=20，稀疏度S=4。根据文献[24]关于算法中参数的选择，SMLG算法、SMHT算法的参数设置为δ=0.1，因此将SMW-HT算法中的参数也设置为δ=0.1，以及关于先验知识的权重矩阵的参数设置为τ=0.5。图9展示的是图片“Elaine”在各种算法下的恢复的视觉效果。

表3 12 张图片在不同感知矩阵算法下恢复的峰值信噪比Table 3 The PSNR of twelve images for different sensing matrices

图9 图片“Elaine”在不同感知矩阵设计算法中恢复的视觉效果Fig.9 The visual result for the recovery of “Elaine” using different sensing matrix algorithms

从以上实验可以看出：对于没有考虑稀疏表示误差的算法SMRAN和SMDCS，图片恢复的峰值信噪比较差。SMLG算法与SMHT算法考虑了稀疏表示误差对于压缩感知系统的影响使得图片恢复的峰值信噪比结果相似，且优于SMRAN和SMDCS算法。SMW-HT算法因为加入了先验知识且考虑了稀疏表示误差，使得峰值信噪比最好且计算复杂度较低。实际应用场景的仿真实验也说明了利用先验知识并同时考虑稀疏表示误差来设计感知矩阵能够提高图片的恢复效果。

4 结 论

对压缩感知系统中的感知矩阵进行设计，设计过程中加入先验知识并同时考虑稀疏表示误差对数据恢复的影响。该先验知识从图片的稀疏表示矩阵中获得。此外，考虑到稀疏表示误差数据量巨大，还对感知矩阵映射下的稀疏表示误差进行估计，以减小计算负担。通过对合成数据和真实应用场景的图片进行仿真实验，证明笔者提出的感知矩阵设计方法可提高数据恢复的准确度。