埋深对双丝拉拔试件动态破裂性能的影响

张亚芳，郭中祥，刘 浩，2，何 娟

1)广州大学土木工程学院，广东广州 510006；2)深圳市市政设计研究院有限公司，广东深圳 518029

钢纤维增强混凝土是由多种材料组合而成的一种典型复合材料. 复合材料的力学性能并不是其各组分材料的简单相加，而是多种材料相互弥补产生的一种协同效应，界面是产生这种效应的主要原因[1-2]. 纤维增强复合材料的整体性能取决于纤维和基体界面的性质，对复合材料的整体力学性能起着至关重要的作用[3]. 在钢纤维增强复合材料中，钢纤维对混凝土的增强效果主要取决于钢纤维-混凝土基体的界面黏结性能[4-5]. CUNHA等[6]研究了纤维埋入长度和角度对纤维拔出行为的影响，通过界面黏结模型逆向分析得到了黏结和滑移的关系. 纤维埋深对水泥复合材料的黏结性能影响显著[7-8]. HONG等[9]研究了纤维与砂浆的界面黏结性能，结果表明，界面的剪切强度随着压应力的增加而增大. ABRISHAMBAF等[10]研究了纤维在持续荷载作用下传递应力的有效性，发现纤维-基体界面预滑移层引起的损伤对纤维长期拉拔行为影响较大. ISLA等[11]研究了不同类型和不同倾角单根钢纤维在不同基体中的拉拔试验，结果表明，纤维倾角和埋深对纤维拉拔强度影响较大.

现有研究主要以静态纤维拉拔的数值模拟和物理实验为主，且多是关于单根纤维拉拔性能的研究[12-14]. 钢纤维增强混凝土破坏是多根纤维被拔出或断裂的复杂过程，在此过程中纤维与纤维间存在着强耦合效应[15]. 由于考虑界面控制的纤维混凝土试件的性能极其复杂，钢纤维双丝拉拔的研究成果较为少见，在动荷载作用下钢纤维双丝拉拔的研究成果更少. 本研究从材料细观非均匀角度出发，利用RFPA2D-dynamics动态分析软件，建立动载作用下不同埋深的钢纤维增强混凝土数值模型，研究埋深变化对动态双丝拉拔过程的影响，可为后续分析多根纤维在混凝土中的耦合效应和作用提供基础.

1 理论分析

本研究从细观角度分别考虑了骨料、水泥基体、钢纤维及界面四相材料的非均匀分布，引入Weibull统计分布函数，描述各相材料物理力学性质的非均匀性，其分布密度函数[16]为

(1)

其中，m为材料的均质度，均质度越高，材料越均匀；x为满足该分布函数的参数(强度、弹性模量和泊松比等)；x0是一个与所有单元参数平均值有关的参数，但其数值并不是平均值.

混凝土材料的损伤过程实质上是能量耗散过程或不可逆热力学过程. 本研究根据Lemaitre应变等效原理，认为受损材料的本构关系[17]可表达为

(2)

σ=E0(1-D)ε

(3)

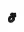
2 数值模型的建立

采用材料破坏过程分析软件RFPA2D-dynamics，用细观力学方法研究复合材料变形和破裂的宏细观行为. 材料破坏准则采用拉伸截断的摩尔库伦准则，其中，最大拉应力准则具有优先权[17].

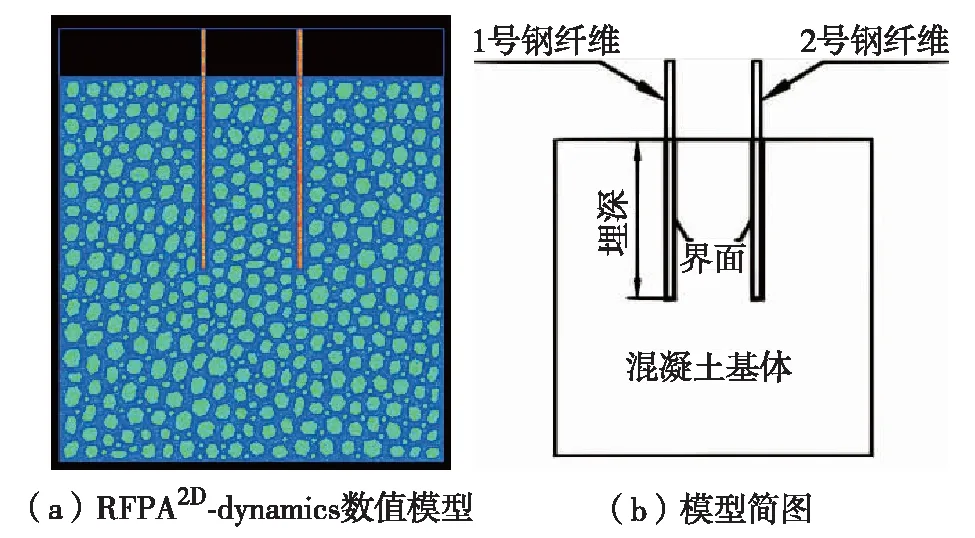
图1 数值模拟模型简图Fig.1 (Color online) Sketch of numerical model

表1为双丝拉拔混凝土试件各相材料的宏观力学参数及均质度[17].

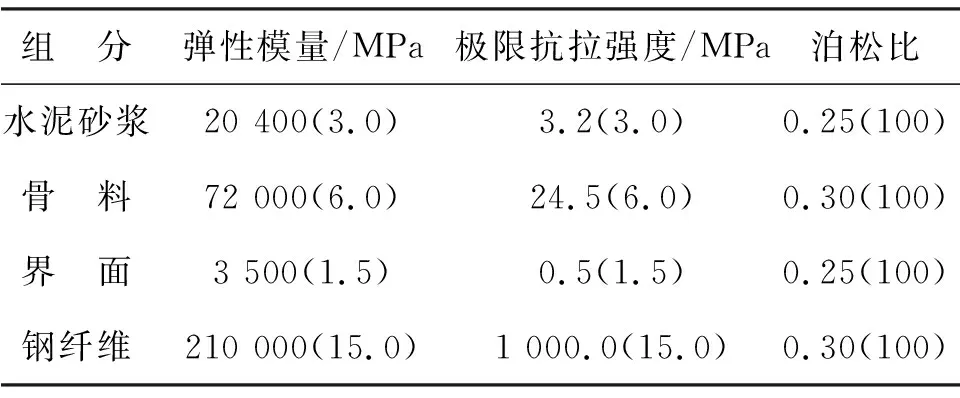
表1 各相材料宏观力学参数及均质度[17] 1)

1)括号内数值代表材料的均质度

图2为动态三角形拉伸应力波，总加载时长20 μs，应力峰值为48 MPa，应力波抬升时间为5 μs，加载速率为9.6 MPa/μs，时间步长为0.1 μs/步，总加载200步.

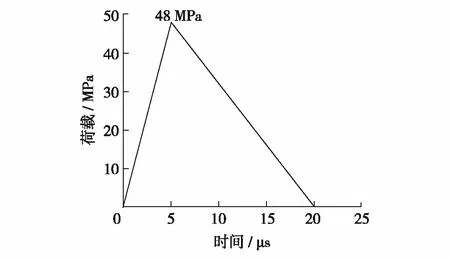
图2 动态加载曲线Fig.2 Dynamic loading curve

3 数值模拟结果分析

3.1 不同埋深下试件的破环过程分析

图3显示了动荷载作用下试件M2、M4和M6的拉拔破坏过程. 在钢纤维顶部施加三角形动荷载，其动荷载在钢纤维内以应力波的形式传播. 钢纤维内的应力波通过界面传至混凝土基体，在内部以圆弧形式不断扩散. 图中越亮区域表示该位置应力值越大. 在加载结束后，由于基体内部还存在残余应力，故基体中光亮处的应力波纹未完全消失.

对动荷载作用下双丝拉拔全破坏过程进行分析可知，该破坏过程大致可分为3个阶段：① 弹性阶段，此阶段时间短暂，界面黏结和传递应力能力良好；② 界面脱黏阶段，此时界面黏结力小于界面剪应力，界面由局部脱黏逐渐到完全脱黏破坏；③ 纤维拔出阶段，界面完全脱黏破坏，小埋深试件双丝各自独立拔出，大埋深试件双丝及双丝间基体共同拔出破坏[18]. 上述破坏过程与赵燕茹[18]在静载作用下界面脱黏的物理实验结论吻合. 通过对试件的破坏全过程图和文献[15]分析对比可知，双丝在拉拔试件动载作用下的破坏模式与静载作用下一致，这与文献[19]的描述吻合. BHUTTA等[19]分别研究了准静态和动态荷载作用下，钢纤维对复合材料基体中界面黏结滑移行为的影响，结果表明，纤维在动态拉拔过程中的破坏模式与准静态拉拔过程没有明显区别.

图3(a)显示了小埋深试件M2的破坏过程. 加载初期(t=2.2 μs)，应力波在钢纤维内部迅速传播，双丝埋入端(钢纤维外露处)附近界面首先出现损伤. 随着应力波的传播，界面脱黏沿纤维纵深方向不断扩展. 由于钢纤维埋深较浅，所以应力波很快传递到钢纤维埋置端(钢纤维深入基体的末端). 在t=5.2 μs时，钢纤维埋置端附近的弱单元首先达到损伤阈值，发生零星破坏. 随着应力波的不断输入(t=7.8 μs)，钢纤维左右界面进一步脱黏，此时钢纤维埋置端已完全脱黏. 加载后期，双丝左右界面完全脱黏，拉拔荷载主要由钢纤维两侧界面的摩擦力承担，这与文献[20]描述一致. 文献[20]认为，纤维-基体界面的脱黏导致界面失效，只有摩擦力阻止纤维的拉拔. 钢纤维埋置端出现空腔，双丝各自被拔出. 小埋深试件承载力较差，破坏模式主要是界面脱黏，表现为双丝各自独立拔出破坏(t=20.0 μs).

图3(b)显示了中埋深试件M4的破坏过程. 双丝埋深变化对加载初期没有明显差异. 随着双丝埋深增加，应力波传至钢纤维埋置端时间(t=9.5 μs)和埋置端脱黏时间(t=11.6 μs)都延后. 在双丝左右界面脱黏的过程中，1号钢纤维的右侧和2号钢纤维的左侧都出现了垂直于钢纤维的裂纹，但是裂纹没有贯通. 由于耦合效应的作用，双丝间一些弱单元首先丧失承载力. 动荷载加载结束(t=20.0 μs)时，双丝间未形成贯通的裂纹，钢纤维埋置端出现空腔. 试件破坏模式主要是界面脱黏，表现为双丝各自独立拔出破坏.

图3(c)显示了大埋深试件M6的破坏过程. 动荷载作用下，加载初期和中期，应力波在试件内的传播和界面剪应力的变化情况与前述大致相同. 在加载后期，钢纤维埋置端附近有大量的弱单元被破坏. 随着埋深的增加，双丝间的耦合效应增强. 在强耦合效应作用下，双丝间的界面剪应力被削弱，1号钢纤维的右侧和2号钢纤维的左侧界面没有完全脱黏.相反，双丝外侧界面剪应力未被削弱，此处界面基本完全脱黏. 随着应力波的不断输入，双丝埋置端附近基体各自萌生一条裂纹，裂纹不断往基体内部横向扩展，最终贯通连接双丝埋置端. 双丝及双丝间的基体共同承担拉拔荷载，说明随着双丝埋深增大，试件破坏时耦合效应随之增强. 试件的破坏模式为双丝埋置端形成贯通的裂纹，双丝及双丝间基体共同拔出破坏.

目的论有三个指导原则，分别是目的原则，连贯原则和忠诚原则。这三个原则之间有先后等级之分，连贯的优先级高于忠诚，同时这两个原则要以目的原则为前提[2]。在该理论的视角下，一切翻译行为都必须首先服从“目的原则”，也就是译文应该根据所要达到的效果进行语言上的组织，同时还应该被目的语读者接受[3]。译文所要达到的效果是译者选择翻译技巧首要需要考虑的因素，也就是效果决定技巧[4]。连贯的核心思想是翻译成果被目的语读者理解，符合其阅读习惯和思维方式。在忠实原则视角下，译文应该最大限度地再现原文的内容和神韵，但是再现程度根据译文所要达到的功能而有所不同。

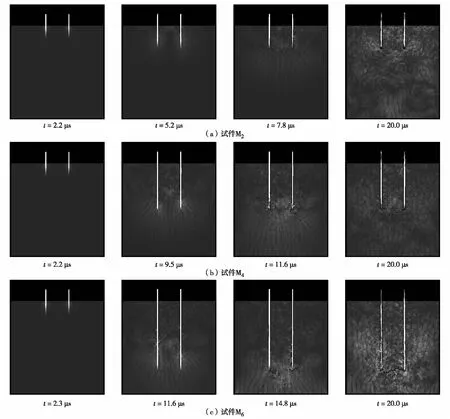
图3 不同埋深下的双丝拉拔试件破坏过程及应力变化Fig.3 Failure process and stress evolution of twin fibers pull-out specimens with various embedment depth

图4为在动载和静载作用下单丝拉拔与双丝拉拔试件的荷载-位移曲线. 由图4(a)和图4(b)拉拔试件分析对比可知，在动荷载作用下单丝和双丝荷载-位移曲线总体变化趋势基本相同，随着埋深的增加，钢纤维拔出位移逐渐减小，大埋深试件出现了振动回弹现象. 究其原因是大埋深试件界面还没有完全脱黏，而动荷载在加载后期是逐渐减小的，此时双丝拔出位移与前期相比较小，弹性变形部分发生了回缩从而产生振动回弹现象.

图4(a)为动载下双丝不同埋深试件的轴向荷载-位移曲线. 由图4(a)可见，不同埋深试件的弹性阶段均很短暂，曲线迅速达到峰值荷载. 曲线到达峰值荷载前，各试件的荷载-位移曲线基本重合，说明埋深变化对钢纤维双丝拉拔混凝土试件弹性阶段宏观力学性能和峰值荷载的影响不大，这与动载下单丝拉拔试件的研究结果[21]相似，如图4(b). 但动载的情况与静载作用却不相同，如图4(c)所示，在静荷载作用下，小埋深试件的曲线斜率小，随着埋深增加，试件整体刚度增大[15]. 同时不同埋深试件的峰值荷载差异显著，埋深越大，拉拔试件的峰值荷载越大；在曲线达到峰值荷载后的劣化阶段，不同埋深试件之间也呈现出不同的差异性[15].

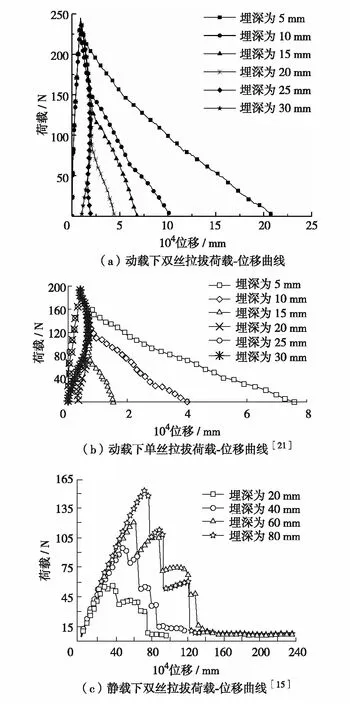
图4 不同埋深试件的荷载-位移曲线Fig.4 Load-displacement curves of specimens with various embedment depth

3.2 声发射行为分析

声发射是材料中局部区域应力集中，快速释放能量并产生瞬态弹性波的一种现象[22]. 声发射是检测材料在荷载作用下损伤和断裂的一种有效方法[23]. TSCHEGG等[24]用声发射技术研究了断裂过程带的范围，并解释了能量耗散的过程. 范向前等[25-26]利用声发射参数累计曲线的转折点，发现预制裂缝尖端粗骨料的存在致使裂缝并非沿着预制裂缝直接向前扩展,而是出现绕道扩展的现象.

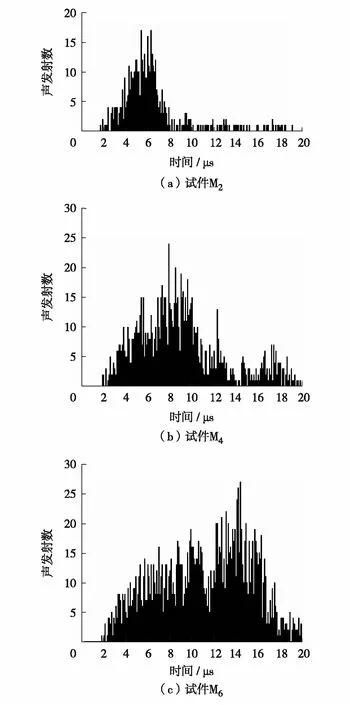
图5 不同埋深试件声发射柱状图Fig.5 Acoustic emission histogram of specimens with various embedment depth

图5为双丝埋深试件M2、M4和M6的声发射柱状图. 由图5可见，由于材料的非均匀性，不同埋深试件声发射柱状图在加载后期出现多个次峰值. 随着埋深增加，试件的声发射数显著增加，且峰值声发射数也不断增多，峰值声发射出现的时间也随埋深增加而延迟. 试件M2在t=5.4 μs出现的峰值声发射数为17，试件M4在t=7.9 μs出现的峰值声发射数为24，试件M6在t=14.4 μs出现的峰值声发射数为27. 说明试件埋深越大，峰值声发射出现的时间越晚，峰值声发射数也越多.

表2为不同埋深试件的峰值声发射数以及峰值出现的时间. 由表2可知，随着埋深增加，峰值声发射数逐渐变多，说明试件耗能效果更好. 双丝埋深增加能有效推迟首次声发射峰值出现的时间，达到试件增韧的效果.

表2 不同埋深试件的峰值声发射数和峰值出现时间

图6为两种不同加载模式下的声发射累积曲线图. 由图6可见，无论动载还是静载作用下，加载初期不同埋深试件声发射累积数量变化不大，加载后期都出现了平台段，声发射累积数量随埋深的增加而不断增多. 动载作用下不同埋深声发射累积数曲线只出现一个平台段，静载作用下声发射累积数曲线出现多处平台段[27]. 究其原因是动载作用下钢纤维附近弱单元大部分在同一个时间段内集中破坏，在加载中后期，虽然应力波在不断输入，但此时的荷载处于卸载状态，未达到单元破坏强度阈值，所以声发射累积数曲线未出现突变和多处平台段. 静载作用下钢纤维附近的单元随着应力波的输入分批次破坏，所以声发射累积数曲线出现突变和多个平台段.

图6(a)为动载作用下的声发射累积数曲线.其中，ci(i=1,2,…,6)为平台转折点，di为加载步终点. 如图6(a)所示，每个试件曲线分为3个阶段：①ab段为应力波加载初期，试件处于线弹性阶段，曲线斜率为0，即各试件声发射累积数为0. ②bci段声发射累积数快速上升，随着埋深逐渐增加，bci段逐渐变长. 此时各试件bci斜率基本一致，即此阶段埋深变化对声发射累积数增加速度影响不大. ③cidi段声发射累积数趋于平缓，随着埋深逐渐增加，cidi段逐渐变短.

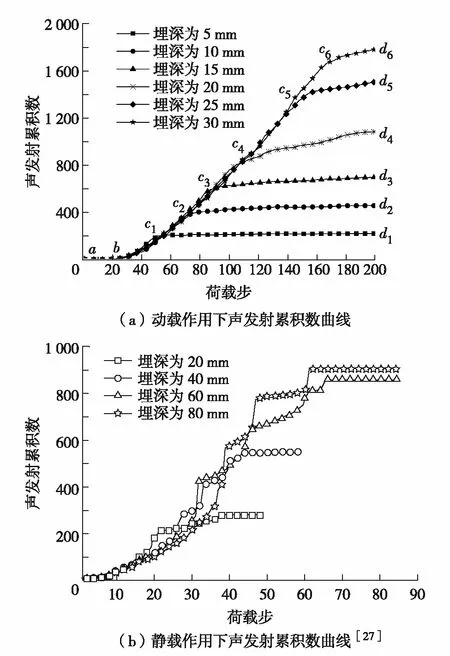
图6 动载和静载加载模式下的声发射累积数曲线Fig.6 Acoustic emission cumulative curves of various load pattern

动载作用下声发射累积数曲线出现平台段，原因是双丝拉拔试件界面基本完全脱黏，钢纤维附近和基体内部没有新的单元破坏. 钢纤维完全脱黏后导致界面失效，动荷载只需要克服滑动摩擦阻力便能把双丝各自拔出使这部分能量消耗掉，这与文献[28]的描述一致.文献[28]认为直线形纤维在脱黏后界面作用力以滑动摩擦为主，拉拔荷载只需克服滑动摩擦产生的阻力便能把纤维拉拔出试件. 声发射累积数随着埋深增加逐渐上升，原因是埋深较大试件在基体内部出现了大量的损伤单元，尤其是大埋深试件更多在纤维埋置端形成一条贯通的裂纹损伤单元. 从能量耗散角度分析，双丝与基体的接触面积增加，拔出过程需要消耗的能量更多. 界面黏结力及滑动摩擦力增加，双丝及双丝间的基体共同受力，混凝土基体单元不断出现损伤，造成试件声发射累积数增加，从整体上提高了试件的耗能水平，达到了增强增韧的效果.

结 论

通过改变试件埋置深度，研究了动载下双丝拉拔过程中埋深变化对试件力学性能的影响，可知：

1)双丝埋深变化对试件破坏模式影响较大. 随着埋深增加，试件破坏模式从双丝各自独立拔出转变为双丝及双丝间基体共同拔出，破坏耦合效应增强.

2)在加载初期双丝埋深变化对双丝拉拔试件的宏观力学性能影响甚微. 随着加载时间的持续，不同埋深试件荷载-位移曲线出现较大差异，大埋深试件出现了明显的振动回弹现象.

3)随着埋深的增加，双丝拔出过程需要消耗更多的能量，双丝及双丝间基体共同受荷，达到了增强增韧的效果.

4)动载作用下双丝埋深变化对试件的峰值荷载影响不大，这点与静载作用下双丝埋深变化对峰值荷载影响较大有显著区别. 在动载作用下随着埋深增加，试件的声发射累积数不断增加，这点与静载作用下双丝埋深变化对试件的影响是一致的.