高低塔斜拉桥辅助墩的优化分析

赵 越，黄平明，范肖波，蔡昌伟，刘修平

长安大学公路学院，陕西西安 710064

斜拉桥由于跨越能力强、主梁抗裂性能好、结构刚度大，已成为跨越大江大河以及深切峡谷的主要桥型. 传统斜拉桥对地形要求较高，难以适用于河谷和山区等边跨地形受限的区域. 高低塔斜拉桥凭借边跨不等跨特点，可有效解决地形受限区域的斜拉桥设置问题[1]. 大跨度斜拉桥一般通过设置辅助墩提高施工阶段稳定性，改善整体结构受力[2-3]，结构优化效果与辅助墩设置位置密切相关，因此对高低塔斜拉桥辅助墩设置进行研究很有必要[4].

目前，对于斜拉桥辅助墩的研究主要集中于传统独塔或等高双塔斜拉桥. 高金萍等[5-6]分析了成桥平衡荷载状态下辅助墩对结构状态的影响，指出大跨度等高双塔斜拉桥辅助墩的设置可以有效减小主梁中跨、边跨以及下塔柱的最大弯矩. 李永兴等[7-8]分析了地震及风荷载下，辅助墩对等高双塔斜拉桥的影响，指出辅助墩能够降低地震作用下的主梁竖向位移及主梁与支座的竖向碰撞力. 喻梅等[9]分析了设置辅助墩对2塔、3塔和4塔斜拉桥静力行为的影响，指出多塔斜拉桥在边跨设置辅助墩可改善结构的受力，提高整体刚度. 高低塔斜拉桥具有一般斜拉桥的基本特点，但由于主塔不对称，结构受力介于独塔斜拉桥与等高双塔斜拉桥之间，辅助墩的设置对结构产生的影响更为复杂. 裴炳志等[10]考虑高低塔斜拉桥的主梁弯矩和位移，指出辅助墩设置在0.3倍边跨跨径处可改善性能. 范肖波[11]研究了恒载以及移动荷载下，辅助墩对高低塔斜拉桥受力特性的影响，认为辅助墩最优位置为距高塔侧边墩0.4倍边跨跨径处. 总体来看，对高低塔斜拉桥的辅助墩设置已有较多研究，但研究选取的结构指标有限，且缺乏明确的综合评价体系. 本研究以高低塔斜拉桥为工程背景，分析移动荷载作用下辅助墩设置数量及位置对桥梁整体受力特性的影响，并选择响应较为明显的指标，基于变异系数法确定各指标权重，进一步通过回归分析拟合单个辅助墩位置对结构整体影响的变化规律，综合评价确定高低塔斜拉桥辅助墩的最优设置区间及最佳辅助墩位置，以期为同类型工程提供参考.

1 工程背景

本研究以一个主跨210.0 m的高低塔中央双索面斜拉桥为工程背景. 桥梁全长378.0 m，桥跨布置为(39.0+73.0+210.0+56.0)m，桥面宽33.5 m. 主梁为C55预应力混凝土箱梁，单箱5室斜腹板截面. 全桥共52对平行钢丝斜拉索，其中，高塔两侧各19对分别为GS1～GS19和GM1～GM19，低塔两侧各7对分别为DM1～DM7和DS1～DS7. 高塔为C55钢筋混凝土独柱塔，塔墩梁固结，高109.5 m. 低塔塔梁固结，桥面以上高度为47.0 m，墩顶设置活动支座，结构总体布置如图1. 其中，SJ1～SJ5为桥墩.

图1 高低塔斜拉桥总体布置(单位：m)Fig.1 Cable-stayed bridge with unequal height towers(unit:m)

为分析辅助墩个数及位置对结构的影响，基于工程背景建立基础有限元模型，进一步根据分析需要对有限元模型进行调整并计算. 采用梁单元模拟主梁及索塔，桁架单元模拟斜拉索并考虑垂度效应. 由于辅助墩位置的改变必然引起结构内力的变化，因此首先要确定合理成桥索力，继而实现合理成桥状态[12-14]. 弯曲能量最小法原理清晰，且确定的合理成桥索力分布均匀，本研究基于此方法确定合理成桥索力. 由于斜拉桥的结构体系确定后，斜拉桥的恒载内力可通过调整斜拉索索力实现内力重分布，但活载内力幅值随索力调整变化并不明显，因此活载作用下的结构受力和变形是影响辅助墩设计合理性的主要因素[9]. 本研究根据移动荷载作用下结构的响应进行辅助墩优化分析.

2 辅助墩对结构响应影响分析

2.1 辅助墩个数对结构响应的影响

首先研究辅助墩个数对高低塔斜拉桥结构受力的影响. 对于高低塔斜拉桥，由于矮塔边跨相对较小，一般辅助墩仅设置于高塔侧边跨内. 因此，结合目标桥梁跨径布置，设置边跨无辅助墩、单个辅助墩和2个辅助墩等3种辅助墩方案. 单个辅助墩方案以实际桥梁辅助墩位置进行计算，两个辅助墩方案参考一般斜拉桥辅助墩设置经验. 对3种方案的有限元模型在移动荷载作用下的响应进行分析，结果如图2至图4. 其中，主梁弯矩以向下为正，主梁位移以向上为正，主塔位移以向小边跨侧为正.

分析结果显示，辅助墩数量改变时，高塔侧边跨主梁弯矩和位移变化较大，中跨变化相对较小，矮塔侧边跨则无明显变化，主梁位移的变化规律与弯矩相似. 辅助墩的设置可有效减小高塔侧边跨和中跨的弯矩及位移. 高塔弯矩在塔根部以及靠近塔顶处差别较大，而低塔弯矩基本不受辅助墩的影响. 主塔位移方面，辅助墩的设置可有效减小高塔上部的位移，而低塔塔顶的位移变化较小，反而低塔塔底部位移有所减小.

图2 辅助墩个数对主梁的影响Fig.2 Influence of different number of auxiliary piers on girder

图3 辅助墩个数对高塔的影响Fig.3 Influence of different number of auxiliary piers on higher tower

图4 辅助墩个数对低塔的影响Fig.4 Influence of different number of auxiliary piers on lower tower

表1给出了不同辅助墩数量时部分响应变化较为明显的指标. 相比无辅助墩，单个辅助墩的主梁边跨最大正弯矩减小了57.4%，2个辅助墩减小了64.4%；单个辅助墩时，高塔侧边跨和中跨最大负位移分别减小了77.4%和13.6%，2个辅助墩时，分别减小了88.7%和15.2%；单个辅助墩的高塔最大弯矩减小了35.5%，2个辅助墩时减小了45.6%.单个辅助墩的高塔塔顶纵向最大位移减小了26.5%，2个辅助墩则减小了28.5%. 总体来看，辅助墩设置数量越多，对结构的改善效果越好，但随着辅助墩数量的增加，结构内力及位移改善幅度明显减弱. 由于辅助墩设置的工期和造价成本较高，综合考虑经济因素，设置单个辅助墩是高低塔斜拉桥受力优化的最经济选择.

表1 辅助墩个数对结构响应的影响

2.2 单个辅助墩对结构受力、变形的影响

为确定单个辅助墩位置不同对结构的影响以及最佳辅助墩设置位置，采取试算方法计算不同辅助墩位置时结构的响应.

由于辅助墩不能距边墩或高塔太近，否则便失去设置意义，因此在高塔侧边跨0.2l～0.8l(l为高塔侧边跨跨度)内， 每隔0.1l设置1个辅助墩，共7个方案进行计算.

图5至图8展示了单个辅助墩位置改变对移动荷载作用下主梁、主塔弯矩、位移以及斜拉索索力增量的影响. 由图5至图8可以看出，单个辅助墩位置的改变对边跨主梁正弯矩和位移影响比较明显，对负弯矩峰值影响相对较弱，边跨弯矩峰值位置随辅助墩位置改变而改变，中跨及矮塔边跨的弯矩位移受到的影响则不明显. 辅助墩位置的改变亦会对高塔塔根弯矩及塔顶位移产生影响，对矮塔的弯矩位移则基本没有影响. 高塔塔根弯矩随辅助墩与过渡墩距离的增大而减小，塔顶位移则随之而增大. 对于斜拉索，辅助墩位置不同时，索力增量变化基本相同，仅有高塔边跨侧最长索GS19的索力增量变化相对明显，但变化幅值也远小于斜拉索的索力.

表2给出了单个辅助墩位置改变时各指标的峰值响应. 由表2可见，各指标最优值出现的位置并不相同.高塔边跨正负弯矩最小值分别出现在辅助墩为0.4l和0.6l处，正负位移出现在0.5l处. 高塔塔根弯矩最小值出现在0.8l处，且与0.7l几乎重合，塔顶位移则在0.4l时最小. 其余指标受辅助墩位置改变的影响相对较弱. 根据分析结果可以初步判断，单个辅助墩位置在0.4l～0.6l较为合适.

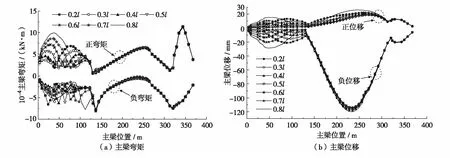
图5 单个辅助墩位置对主梁的影响Fig.5 Influence of different auxiliary pier position on girder

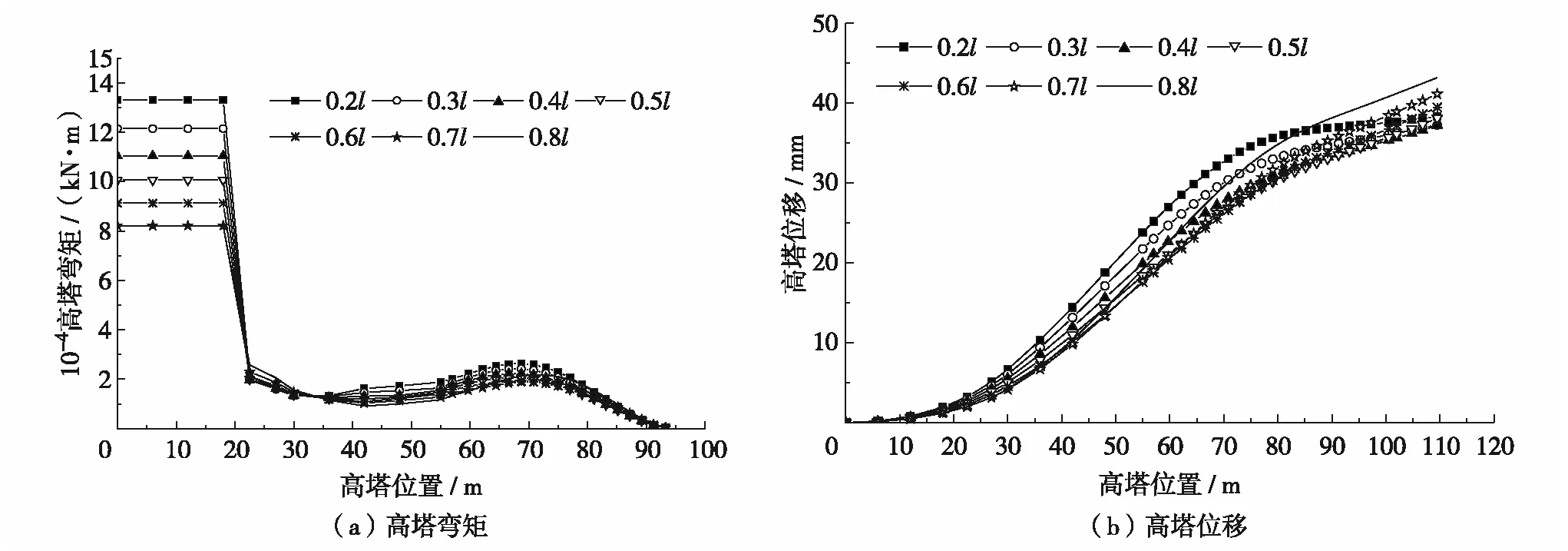
图6 单个辅助墩位置对高塔的影响Fig.6 Influence of different auxiliary pier positions on higher tower

图7 单个辅助墩位置对低塔的影响Fig.7 Influence of different auxiliary pier positions on lower tower

表2 单个辅助墩位置对结构内力的影响

Table 2 Influence of different auxiliary pier position on structure response

位置边跨最大正弯矩/(kN·m)边跨最大负弯矩/(kN·m)中跨最大正弯矩/(kN·m)中跨最大负弯矩/(kN·m)边跨最大正位移/mm边跨最大负位移/mm中跨最大正位移/mm中跨最大负位移/mm高塔塔底弯矩/(kN·m)低塔塔底弯矩/(kN·m)高塔塔顶位移/mm低塔塔顶位移/mm0.2l69 143-65 766114 325-78 08113.3-21.221.8-118.0133 18115 94338.3-36.00.3l58 283-59 601113 489-78 2589.8-15.319.8-115.5121 46015 94637.3-36.00.4l49 576-63 128113 019-78 5516.9-10.318.9-114.0110 36415 95237.2-36.10.5l57 903-60 134113 063-79 0334.8-8.419.0-113.8100 58515 96238.1-36.20.6l72 316-54 005113 531-80 0186.9-13.620.0-114.791 22715 97739.5-36.50.7l86 451-59 707114 425-81 60310.6-20.222.1-116.782 13516 00841.2-36.90.8l99 579-77 938115 779-83 55515.5-28.626.0-120.182 08415 94842.5-37.3

图8 单个辅助墩位置对斜拉索索力增量的影响Fig.8 Influence of different auxiliary pier position on cable tension force

2.3 结构动力特性的影响

结构自振频率反映了其基本的动力特性，斜拉桥的动力特性同样受辅助墩位置的影响[15]. 表3为辅助墩数量及位置对结构前5阶频率的影响.由表3可见，辅助墩的数量对高低塔斜拉桥结构频率产生较为明显的影响，辅助墩数量越多，结构的刚度越大. 单个辅助墩位置改变时， 0.4l～0.6l的结构一阶频率相对较大，呈现先增后降趋势，但结构频率的整体变化幅度较小.

3 最优辅助墩位置

目前针对辅助墩设置位置的相关研究虽有不少，但主要以试算方式进行. 由于计算工作量大，采用试算方法进行分析时选择的参数组合有限，最终位置选择的好坏与试算参数选取有很大关系. 并且，由于不同指标的响应情况不一致，无法单纯地以某一个指标的好坏进行选择，需要综合考虑结构各指标响应，给出最优辅助墩的位置. 因此，本研究采用结合麦考特法的全局优化算法[16]， 选取响应较为明显的指标，基于回归分析拟合目标函数，最终确定最优的辅助墩位置.

表3 辅助墩设置位置不同时结构频率的对比

选取受辅助墩位置改变影响较为明显的边跨最大正负弯矩及正负位移、高塔最大弯矩及位移作为控制指标，基于结构不同指标的响应情况，采用变异系数法确定各指标的权重[17]，如表4.

表4 指标变异系数及权重

然后计算关键指标响应的加权总计值.由函数自变量即辅助墩位置和对应的加权总计值，可得到拟合回归方程为

F(x)=-11 954.4+102 672.2x-9.3/x-

10.6x2-476.1/x2-214 448.0x3+

1 134.2/x3+179 208.3x4-163.1/x4

(1)

其中，F为各指标的加权总计值；x为辅助墩与边跨过渡墩的距离.

图9 拟合曲线与实际值的对比图9 Comparison of the weighted total value of the fitting function with the actual value

最终得到的拟合函数与实际加权总计值对比情况如图9. 由图9可见，拟合函数理论值与实际值拟合较好，相关系数为0.99，拟合度较高. 进一步利用优化算法，求得目标函数的最小值出现于辅助墩位置0.446l处，即辅助墩设置的最佳位置. 根据拟合曲线可看出，辅助墩位置在0.4l～0.5l时，目标函数的响应值十分接近. 在实际工程中受制于地形，根据辅助墩位置的分析结果在合理范围内进行选择，可以最大程度保证辅助墩设置的优化效果. 本研究工程项目受地形限制，且要保证通航需求，最终将辅助墩位置选择于距过渡墩0.348l处. 该处目标函数值相比最优辅助墩位置的目标值有一定差异，高出约3.71%.

4 结 论

综上研究可知：

1)设置辅助墩可以明显降低高低塔斜拉桥边跨主梁及高塔的弯矩和位移，对中跨及矮塔的影响则有限. 但增加辅助墩个数的改善效果相比单个辅助墩大幅减弱，综合考虑设置单个辅助墩是经济的选择；

2)单个辅助墩位置的改变对边跨主梁弯矩和位移影响比较明显，高塔的弯矩和位移亦受辅助墩位置的影响，高塔最大弯矩随辅助墩位置与过渡墩距离的增大而减小，高塔最大位移则随之增大而增大，结构频率及索力增量总体变化较小；

3)单个辅助墩最佳设置位置为与高塔侧距边墩0.446l处，但当辅助墩位置位于0.4l～0.5l内时，位置改变带来的优化效果变化并不明显；

4)针对试算方法参数组合有限的问题，选取响应明显的指标，基于变异系数和回归分析，确定最优辅助墩位置. 评价指标可根据需要灵活调整，研究结果可为同类型桥梁设计提供参考.