尺寸不规则度梯度分布参数对泡沫金属单轴拉伸力学性能的影响研究
胡和平,谢 帅,张晓阳,刘希文
(南华大学 土木工程学院,湖南 衡阳 421001)
0 引 言
泡沫金属兼有结构与功能材料的特性,具有质轻、高比强度和刚度以及优良的物理性能,在汽车、航空航天和建筑等行业具有广泛应用,其力学性能受到广泛关注[1-3]。目前,国内外泡沫金属力学性能的研究多集中在准静态压缩和冲击条件下的试验[4-7],对于泡沫金属拉伸性能方面研究较少。韩春光等[8]提出泡沫金属的拉伸破坏是由拉伸后期的细观结构破坏引起的,早期拉伸的非线性特征是由材料的非均匀性引起的。项苹[9]对泡沫金属的拉伸变形特征和机理进行实验研究,发现泡沫金属的拉伸变形特征具有较为明显的三阶段特征。
泡沫金属的细观结构对其力学性能有显著影响,为定量描述细观结构的胞孔形状、尺寸以及分布的随机程度,国内外学者提出了各自的不规则度参数定义[10-11]。L.Q.Tang等[11]首次对细观结构的每个胞孔提出两个不规则度变量:形状不规则度和尺寸不规则度,采用不规则度变量的统计参数描述细观结构的胞孔特征;根据该定义,细观结构越均匀,形状不规则度和尺寸不规则度均值越小;该定义能更好地反映泡沫材料细观结构的分布特征。L.Q.Tang等[11]等研究发现,影响泡沫金属压缩力学性能的是细观结构的形状不规则度,尺寸不规则度不影响泡沫金属单轴压缩的力学性能。然而,该结论缺乏三维模型的验证,尺寸不规则度是否影响泡沫金属单轴拉伸力学性能尚未研究。
Z.J.Zheng等[12]研究不同加载速率条件下细观结构不规则度对力学性能的影响,基于2D泡沫细观结构研究动态变形特征,提出了三类变形模式:准静态变形模式、过渡变形模式和冲击变形模式,并发现模型的细观结构不规则度显著影响变形模式的临界速率。王根伟等[13]研究负梯度的3D Voronoi在不同速度冲击下的力学性能,也发现模型变形符合郑志军提出的三类变形模式。L.Q.Tang等[14]研究了形状不规则度组合的2D Voronoi模型在不同速率冲击压缩条件下的力学性能,结果表明,不同形状不规则度组合结构对泡沫金属压缩应力-应变曲线和能量吸收影响显著,存在最优解。然而,不规则度连续梯度变化的三维模型的力学性能尚未明确。
泡沫金属实际应用时,往往承受多轴复杂加载工况,发生拉伸破坏、剪切破坏、屈曲等破坏形式,因此,泡沫金属拉伸力学性能研究必不可少。本文定量研究了泡沫金属尺寸不规则度梯度参数对其单轴拉伸力学性能的影响;对比形状不规则度相同尺寸不规则度不同的3D Voronoi模型结果,探究尺寸不规则度参数对泡沫金属力学性能的影响。这些研究将阐明尺寸不规则度是影响泡沫金属力学性能的重要因素,完善细观结构对多胞材料力学性能的影响研究,有助于多胞材料的优化设计。
1 模型建立及其合理性检验
1.1 模型的建立
本文尺寸不规则度连续梯度变化3D Voronoi模型的建模方法是:基于修改的voro++程序[15],改变种子数量和控制种子间最小间距函数d(x),例如沿着x方向梯度变化的模型,在坐标x数值处的种子间最小距离函数表达式如下:
d(x)=l0+a·x/w0
(1)
其中l0控制最小(或最大)距离;a控制梯度变化参数,当a=0时,表示非梯度变化模型,当a≠0表示连续梯度变化的模型;w0为模型沿梯度方向,即x方向的边长(本文取值w0=30 mm)。定义梯度参数k:
k=a/d0
(2)
其中d0表示3D Voronoi模型的平均等效直径,通过控制种子点数量N和模型体积V0实现,关系式如下:
(3)
梯度参数k越大,表示沿着梯度方向,细观结构胞孔尺寸不规则度差异越大。控制变量V0,N,a,l0,w0的不同取值,建立不同尺寸不规则度梯度参数的3D Voronoi细观模型。
1.2 合理性检验
泡沫金属单轴拉伸数值模拟采用Abaqus/Explicit,有限元模型如图1所示。采用一对解析刚体便于荷载施加,模拟加载装置,其中一块解析刚体以恒定速度(15 mm/s,0.5/s)加载,另一解析刚体固定。单轴拉伸时,泡沫金属内部接触设置为通用接触,摩擦系数为0.02,允许接触分离;泡沫金属与解析刚体接触设置为面面接触,摩擦系数为0.02,不允许接触分离。泡沫金属基体材料为纯铝,基体材料参数、计算参数和模型参数采用文献[16]推荐的数值,保证有限元既有较高的精度,又具有较快的计算效率。有限元模型的合理性已被泡沫金属单轴拉伸、单轴压缩、双轴拉伸试验结果验证[17]。
为了保证计算结果合理,伪应变能与内能的比值不能超过10%,动能与内能的比值不应超过5%。图2为梯度模型单轴拉伸能量比值曲线,从图2中可以看出,伪应变能/内能、动能/内能数值均小于5%,说明有限元模型数值模拟结果是合理的。
2 梯度参数单轴拉伸影响分析
表1为建模控制参数和不规则度统计参数,模型的形状不规则度和尺寸不规则度可以通过L.Q.Tang[11]对其提出的定义来计算,模型细观结构如图3所示。随着梯度参数k增大,泡沫金属的形状不规则度平均值和方差均减小;尺寸不规则度平均值和方差的绝对值均先减小后增大。形状不规则度与尺寸不规则度均值越小,说明模型的细观结构越均匀。图4为梯度参数(k=3/3.22)模型的单轴拉伸变形结果。图4(a)为初始状态下单轴拉伸变形图,继续拉伸发现模型先从胞孔较大的地方开始拉裂如图4(b),进一步拉伸形成一条横贯于加载方向的断裂带如图4(c),呈现明显的局部变形,变形并不均匀。图5为梯度参数(k=3/3.22)模型不同方向的尺寸不规则度空间分布图,从图5中可以看出,梯度方向(x方向)有明显的梯度空间分布,呈线性关系,其他两个方向无明显线性关系。
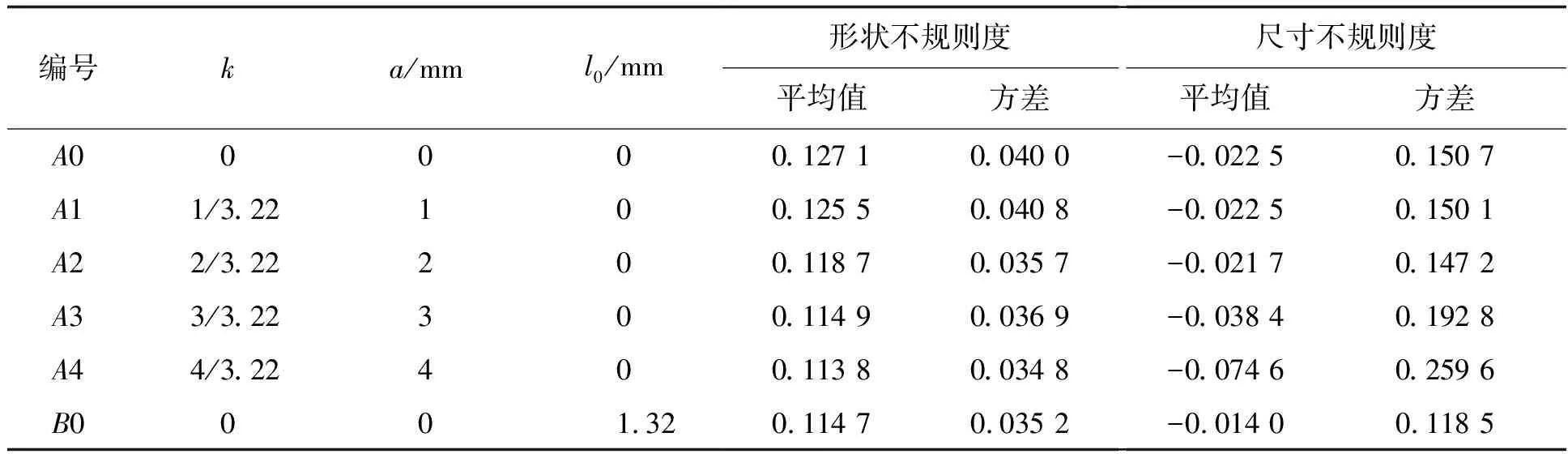
表1 建模控制参数和不规则度参数统计
图6为梯度参数(k=3/3.22)模型的三个方向单轴拉伸应力-应变曲线。可以看出x方向的屈服强度小于其他两个方向的屈服强度,y与z方向的屈服强度基本一致,这验证了模型的横观各向同性。
图7(a)为不同梯度参数模型x方向的单轴拉伸应力-应变曲线,表2为不同梯度参数模型屈服强度和破坏强度的单轴拉伸结果,沿着梯度方向,梯度参数显著影响模型的单轴拉伸屈服强度,但并非单调变化,存在最优解,梯度参数k为0~2/3.22时,屈服强度随着梯度参数的增加而缓慢增加,之后逐渐下降。梯度参数(k=0)模型的破坏强度明显大于梯度参数(k=3/3.22)模型的破坏强度,图8(a)、(b)为梯度参数(k=0)和梯度参数(k=3/3.22)模型x方向的拉伸破坏截面图,从图中可以看出颜色越亮,应力越大,越容易产生断裂带,且梯度参数(k=0)模型的应力分布较均匀,梯度参数(k=3/3.22)模型在断裂带处应力集中现象较为明显。梯度参数(k=0)模型的断裂带所经过的胞壁明显多于梯度参数(k=3/3.22)模型断裂带经过的胞壁,拉伸破坏强度比之更大。

表2 不同梯度参数模型的单轴拉伸结果
图9为x方向屈服强度和破坏强度的拟合曲线,拟合函数如下:
σs=3.75+1.26k-1.47k2
(4)
σb=4.09+1.31k-1.57k2
(5)
其中σs表示屈服强度,σb表示破坏强度。
图7(b)为不同梯度参数模型y方向单轴拉伸应力-应变曲线,发现尺寸不规则度梯度参数对其峰值应力有显著影响,梯度参数(k=3/3.22)模型的破坏强度明显大于梯度参数(k=0)模型的破坏强度。图8(c)(d)为梯度参数(k=0)和(k=3/3.22)模型y方向拉伸截面破坏图,两个模型的应力分布都较为均匀,梯度参数(k=3/3.22)模型的断裂带所经过的胞壁多于梯度参数(k=0)模型断裂带经过的胞壁,其拉伸破坏强度更大。
3 尺寸不规则度的影响分析
本文提及的A3和B0为形状不规则度相似而尺寸不规则度不同的模型。图10为两个模型的单轴压缩应力-应变曲线,发现A3模型x方向的应力应变曲线具有五阶段特征,分别为线弹性阶段、应力下降阶段、应力上升阶段、平台应力阶段和密实阶段,与随机分布模型的三阶段特征(线弹性阶段、平台应力阶段和密实阶段)相比,有明显的区别。梯度变化方向上,模型的应力-应变曲线差异明显,非梯度变化方向上,尺寸不规则度不同对其应力-应变曲线影响不显著。图11为两个模型的单轴拉伸应力-应变曲线,尺寸不规则度不同对其应力-应变曲线影响显著。梯度变化方向上,梯度模型的强度明显小于随机分布模型的强度,非梯度变化方向上,梯度模型的拉伸强度比随机分布模型的强度稍大,说明尺寸不规则度不同对模型的拉伸强度影响显著。图12为A3和B0模型不同方向的拉伸破坏截面图,可以看出A3模型梯度方向胞孔局部变形显著(图12(a)),而A3模型非梯度方向(图12(b))和B0模型y方向(图12(c))应力分布比较均匀,胞孔局部变形现象不显著。
4 结 论
1)不同梯度参数模型单轴拉伸时,沿梯度方向胞孔局部变形显著,梯度参数影响模型梯度方向和非梯度方向的单轴拉伸屈服强度和破坏强度,且对梯度方向影响尤其显著,呈二次函数关系,存在最优解。
2)形状不规则度相似尺寸不规则度不同的模型,单轴拉伸时,梯度方向胞孔产生局部变形,梯度方向受尺寸不规则度参数的影响比非梯度方向更明显,且比均匀模型和梯度模型非梯度方向胞孔变形更加显著;梯度泡沫金属单轴拉伸时胞孔局部变形显著,细观结构应避免过大胞孔结构或对大胞孔进行局部强化将显著提高其拉伸性能。
3)不同于单轴压缩,尺寸不规则度参数是影响单轴拉伸力学性能的重要结构参数。本文研究完善了多胞材料细观力学性能研究,有助于泡沫金属材料及其复合材料的优化设计。

