基于森林资源连续清查数据的西南地区云南松林分生长模型研究

涂宏涛，李 华，张成程，马国强，宋 放

(1.国家林业和草原局昆明勘察设计院，云南 昆明 650216；2.四川省林业和草原生态环境监测中心，四川 成都 610081)

云南松(Pinusyunnanensis)作为西南地区最主要的用材树种之一，分布在北纬23°～29°，东经98°～106°范围[1]，适宜海拔 1 000～3 200 m，主要分布区域在云南省。林分生长模型是反映林分生长与林分状态和立地条件的关系函数[2]。目前，林分生长模型主要分为平均胸径生长模型、平均树高生长模型和蓄积量生长模型等[3]。通过建立模型，可以模拟林分生长规律，预估林分生长和收获。本文以全国第九次森林资源连续清查云南省清查的云南松固定样地数据为研究对象，以林分胸径、树高、年龄、立地指数、林分密度为因子建立了云南松林分树高、林分立地指数、林分断面积生长和林分收获等模型，为科学合理地经营云南松林提供科学参考[4-7]。

1 数据来源与方法

1.1 数据来源

本研究实验数据采用2017年的全国第九次森林资源连续清查云南省清查568块云南松纯林的固定样地数据，该固定样地是从云南省范围内按6 km×8 km均匀布设的边长28.28 m、面积0.08 hm2的 7 974 块正方形固定样地中选取的。

1.2 模型的选取

目前，全林分生长模型是通过林分调查因子林分平均高H、林分优势木平均高HT、林分平均胸径D、林分每公顷株数N、林分平均年龄A等来拟合林分密度指数SDI模型、林分立地指数SI模型、林分总断面积G模型和林分收获(蓄积)M模型。选取以下模型进行拟合[8-10]。

1)林分平均胸径—林分平均树高模型：

①H=a·Db；②H=a·ebD；

③H=a·D2+b·D+c；④H=a·ln(D)+b

2)林分优势木平均高HT模型：

①HT=a+b·A+c·A2；②HT=a+b·A；

③HT=a·Ab；④HT=a·EXP(-b/A)

3)林分密度指数模型：

SDI=N·(Do/D)-b

4)林分立地指数模型：

SI=HT·EXP(-b/Ao)/EXP(-b/A)

5)林分总断面积G模型：

G=a·SIb·EXP(c·(SDI/1000)d/A)

6)林分收获(蓄积)M模型：

LnM=a+b/A+c·SI+d·LnG

式中：Do为标准平均直径；Ao为基准平均年龄；a、b、c、d为模型参数。

1.3 数据处理

云南松林固定样地按照不同龄级、不同郁闭度、不同林分平均高等选取，主要林分调查因子特征见表1。共收集568块云南松林样地数据，利用2/3(379块)样地数据参与建模，1/3(189块)样地数据用于模型检验。

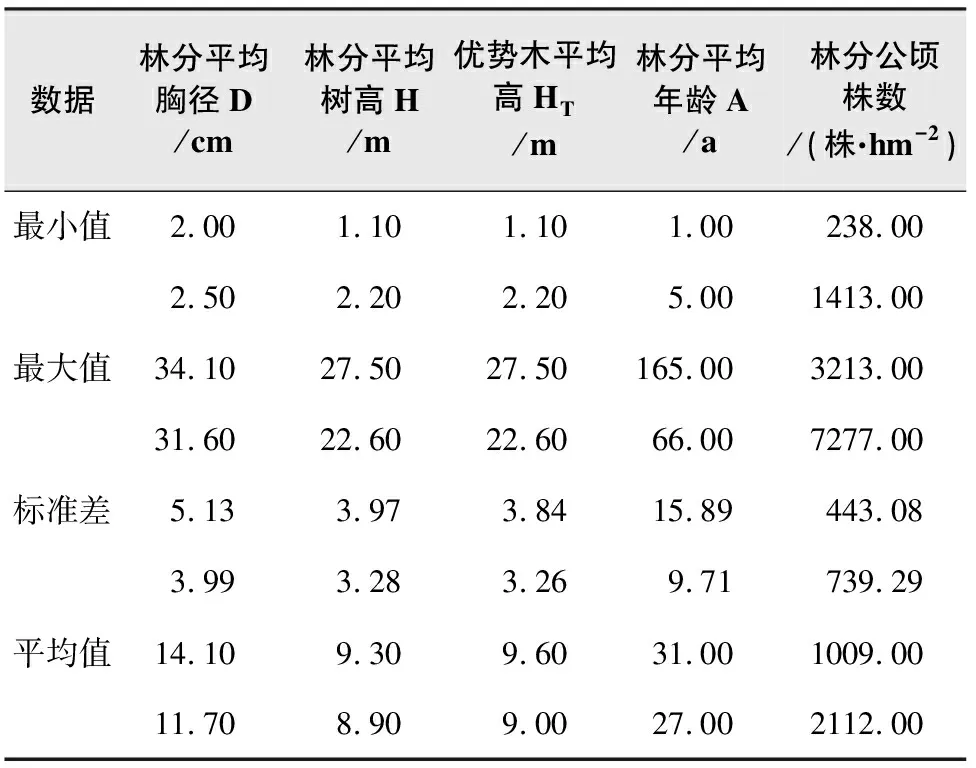
表1 云南松林主要林分调查因子

1.4 模型评价与检验

对建模样本进行检验，计算检验指标，评价模型优度。用于模型评价与检验的指标主要有R2(拟合优度或判断系数)、P(预估精度)、SEE(剩余标准差)、平均相对误差(E)、平均相对误差绝对值(e)。R2、P越接近1越好；SEE、E、e越接近0越好[11-12]。

(1)

(2)

(3)

(4)

(5)

2 结果与分析

2.1 胸径—树高模型

树高和胸径是林分测树中最基本的因子，通过建立二者之间的关系模型，可以反映林分树木的动态生长变化，其模型如图1：

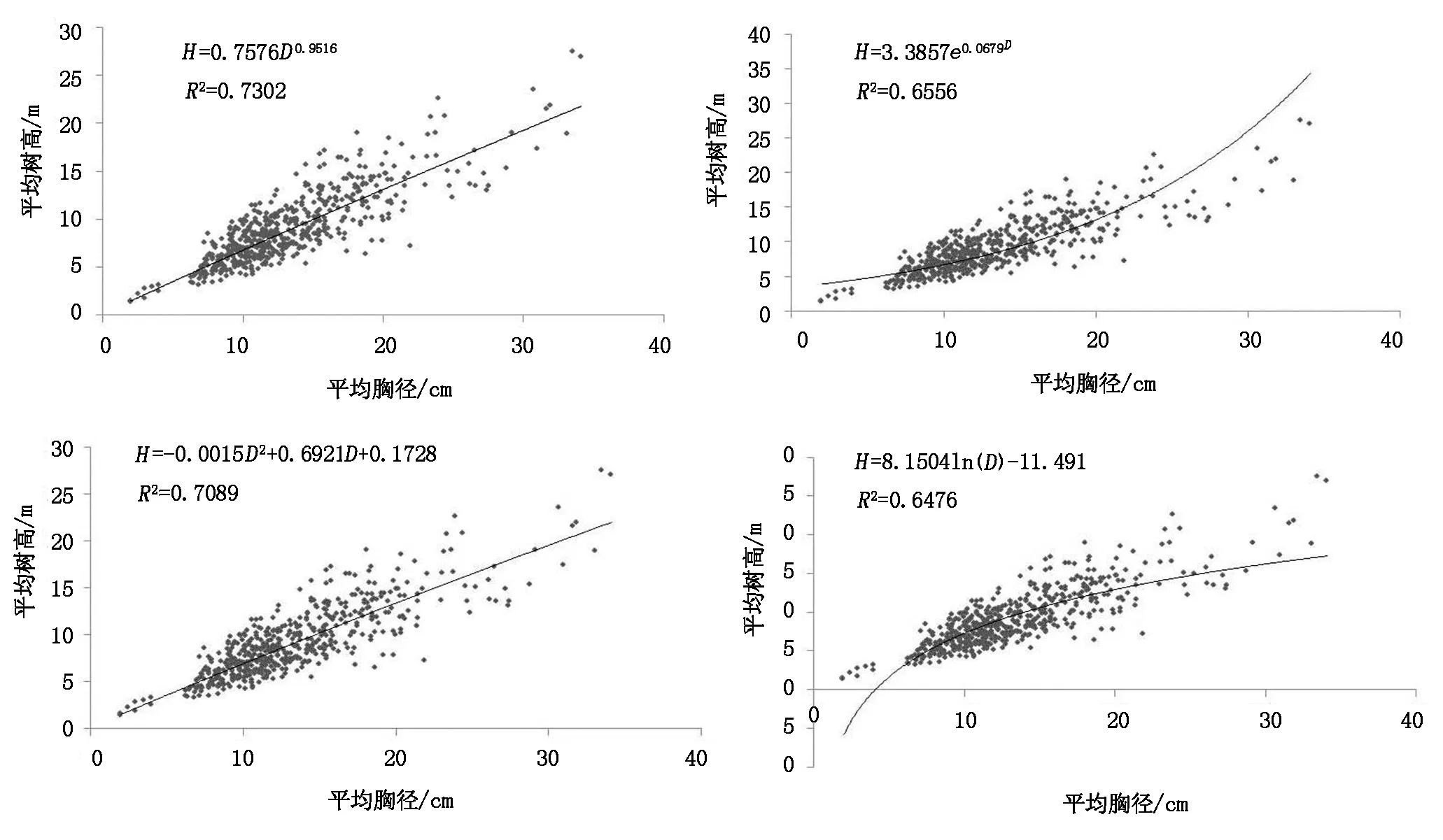
图1 云南松林样木胸径与树高模型

由图1可以看出,H=0.757 6D0.951 6模型的R2值最高，其模型拟合效果最佳，这也与目前研究发现胸径与树高的幂函数模型拟合效果最佳相一致。

2.2 林分密度指数模型

林分密度指数SDI是指林分的现实株数转化为标准平均直径D0时所具有的单位面积林木株数。根据图1胸径—树高散点图及拟合模型，可得其大致趋势，并研究得出其标准平均直径D0=10 cm。

林分密度指数计算函数为：SDI=N(10/D)b

式中：N为林分公顷株数，D为林分平均胸径，b为参数(根据赖内克研究认为同一树种、同一经营历史的林分，林分完满立木度株数和平均直径之间的关系函数均有相同的斜率，b=-1.605，因此，本研究中林分密度指数函数b也取-1.605)；即SDI=N(10/D)-1.605。

2.3 林分优势木平均高模型

优势木平均高是重要的林分调查因子，是表现林分生产潜力的重要数据，是林分立地条件好坏的重要指标，因此可通过林分优势木平均高模型来倒推林分立地指数(表2)。

表2 林分优势木平均高模型因子

由表2可知，优势木平均高最优模型为：

HT=1.5364×A0.5456

式中：HT为林分优势木平均高，A为林分平均年龄。

优势木平均高的Schumacher模型为:

HT=17.2316×EXP(-15.378/A)。

对以上2模型的优势木平均高实际值与理论值进行T检验，结果如表3。

表3 林分优势木平均高实际值与理论值T检验

注：t为实际值与理论值T检验的检验值；df为自由度；p为显著概率值。

由表3看出，林分优势木平均高实际值与理论值T检验t值为 0.720 2、1.411，自由度=189-1，显著性概率p为 0.472 3、0.159 9均大于0.05，差异性不显著，因此，本研究所建立的林分优势木平均高模型检验值符合精度要求。

2.4 立地指数模型

立地指数是在某一立地上特定基准年龄时林分优势木平均高度值，是直观地反映立地质量的数量指标。林分立地指数可通过优势木平均高来体现，一般采用林分优势木平均高Schumacher模型，林分优势木平均高与立地指数间的关系表达式为：

SI=(HT×EXP(-b/Ao))/EXP(-b/A)

b值取林分优势木平均高Schumacher模型中参数b值为15.378，基准年龄为10 a，最终林分立地指数模型方程为：

SI=(HT×EXP(-15.378/10))/EXP(-15.378/A)

式中：SI为林分立地指数，A为林分平均年龄。

2.5 断面积生长模型

林分断面积是直接反映林分收获量的重要指标，其预测值的多少直接影响森林经营决策，研究表明，一般以林分密度指数作为自变量的Schumacher模型的模拟精度最高，因此，本研究采用Schumacher模型对数据进行拟合，公式为：

G=a×SIb×EXP(c×(SDI/1000)d/A)

其中SI=(HT×EXP(-15.378/10))/EXP(-15.378/A)，SDI=N(10/D)-1.605

式中:HT为林分优势木平均高，A为林分平均年龄，N为林分公顷株数，D为林分平均胸径，a、b、c、d为参数。

将G(林分断面积)模型中SI、SDI求出后，利用R软件拟合各参数值，拟合结果为：a=12.080，b=0.82，c=-38.856，d=-1.15，R2=0.746，一般实际中G可通过G=π/40000×N×D2来计算。因此，对G模型方程进行T检验，结果表明：t值为-4.829 9，p=0.283﹥0.05，差异性不显著，模型检验值符合精度要求。

2.6 林分收获模型

林分收获模型通过林分立地指数、林分平均年龄和林分断面积三者之间的函数来反映林分蓄积量。本研究采用Schumacher模型方程对M(林分收获)模型进行拟合，公式为：

LnM=a+b/A+c×SI+d×LnG

式中：M为林分总蓄积量，SI为林分立地指数，G为林分断面积，A为林分平均年龄，a、b、c、d为模型参数。

林分总蓄积量一般采用计算式为：M=f·H·G

式中：f为形数，云南松平均形数f为0.45，H为林分平均高，G为林分断面积。

通过R软件对LnM模型各参数进行拟合，其结果为：a=0.902，b=-13.094，c=0.125 8，d=1.194，R2=0.953 2。

此外，对LnM模型进行T检验，结果表明：t值为 5.605 8，自由度=189-1，显著性概率p=0.730﹥0.05，差异性不显著，模型检验值符合精度要求。因此，林分收获模型表达式为：

LnM=0.902+(-13.094)/A+0.125 8×SI+1.194×LnG。

3 结论与讨论

本研究以森林资源连续清查云南松固定样地林分调查数据为基础，系统研究了西南地区云南松林平均树高、林分断面积、林分立地指数和林分蓄积量因子与林分平均年龄、林分优势木平均高、林分公顷株数等的关系，在此基础上，建立了云南松林分断面积和林分收获预估模型。

模型拟合结果表明，所有建立的模型T检验的p值均大于0.05，差异性不显著，其精度均符合要求。其中，林分收获模型的预估精度最高达到90%以上，模型具较高的精确度和稳定性，可以应用于本地区云南松林的经营管理和收获预估。能够为西南地区云南松林的科学经营提供理论基础，并对其营林措施的制定具有重要意义。

虽然建立的模型符合精度要求，但未区分人工林与天然林之间的差异，加之模型拟合数据量不够，可能会存在一定的差异，在今后的研究中有待进一步探究。