冻融条件下水工混凝土渗透性演化试验研究
谭 鹏,程庆超,童富果
(1.三峡大学水利与环境学院,湖北 宜昌 443002;2.浙江华东建设工程有限公司,浙江 杭州 310014)
0 引 言
混凝土面板作为混凝土面板堆石坝的重要防渗结构,大坝的安全稳定和运行寿命与面板的渗透性直接相关[1]。我国北方地区多个混凝土面板堆石坝工程实践表明,冻融破坏是促使混凝土防渗性能弱化和使用寿命缩短的原因之一[2-5],遭受冻融破坏的混凝土面板会表现出不同规模的表面剥落和裂纹损伤、张裂等情况[6]。混凝土面板的渗透性与其自身的水胶比、粉煤灰掺量以及引气剂含量等因素相关,同时也受到冻融作用的影响。
水渗透性测试相比透气性和离子渗透性检测,其测试方法简单、直观、较为可靠,且混凝土只要具有良好的抗水性,通常就可以满足抗渗性的要求[7],因此,国内外针对混凝土渗透性的研究着重于透水性。现行主要的水渗透试验方法主要有稳定流动法、抗渗标号法和渗透深度法。稳定流动法通过测定流过混凝土的流速以及流量,再依据达西定律求得其渗透系数,然而,由于该方法要求试验在稳定且缓慢的单向流中进行,致使试验误差较大[8];抗渗标号法是我国目前采用的抗渗指标,但该方法不便于在水工建筑物上使用[9];渗透深度法适用于低渗透性的混凝土,并且对于一些采用表面处理的混凝土并不适用[10]。近年来,Autoclam测试方法[11]因其耗时短,能快速、较好反应一般混凝土的渗透性能,得到了大量的应用。但是,该方法也存在一定的不足之处:测试接触面无法保证固定统一,对测试结果影响较大;该方法没有考虑测试试件的尺寸影响;由于冻融破坏的作用,导致仪器与混凝土表面的密封性得不到保证等。
基于此,本文采用室内快速冻融试验和Autoclam渗透性测试仪,解决了Autoclam渗透性测试仪与冻融后试件接触面的密封性无法保证等问题,对常见水工混凝土水胶比、加引气剂、掺粉煤灰等工况进行冻融循环下的渗透性试验,研究了受冻融破坏后混凝土的渗透性演化规律,探索了渗透性与抗压强度之间的相关性,为混凝土受冻融破坏后的特性测评提供参考。
1 水渗透性测试试验
1.1 试验原材料及混凝土配合比
根据谢凯军等人[12]提出的,寒冷地区坝体外部上、下游水位变化区及以上部位水工混凝土的水胶比应尽量控制在0.45~0.55范围内的要求,本文设计0.47、0.50、0.53三种水胶比工况,混凝土配合比见表1。
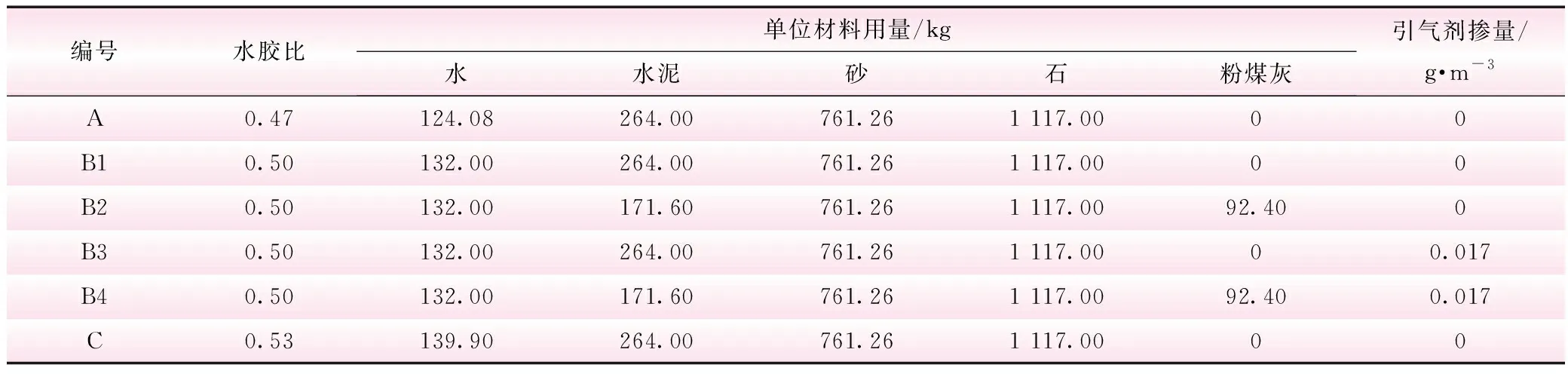
表1 混凝土设计配合比
水泥为P.O 42.5华新普通硅酸盐水泥;粉煤灰为襄阳发电厂生产的Ⅱ级粉煤灰;细骨料为人工砂,细度模数为2.71,属中砂;粗骨料为花岗岩碎石,粒径5~20 mm;减水剂为高效聚羟酸减水剂,引气剂为江苏苏博特新材料公司生产的AIR202型引气剂,取实验室自来水作拌和用水。
1.2 试验测试原理及方法
传统测试混凝土渗透性的方法多种多样,常见评价混凝土渗透性的方法主要以水、气、离子的渗透情况以及利用抗压强度来表征混凝土的渗透性[11,13]。本文采用依据达西定律推导的多孔介质渗流毛细管模型,运用稳定流态法推求材料的渗透系数,即
(1)
式中,Kq为相对渗透系数;Q为渗水量;a为混凝土吸水率;T为恒压所用时间;H为试件静水压力;A为测试试件横截面积。
按照表1所示设计配合比,结合GB/T 50081—2002《普通混凝土力学性能试验方法标准》,每组浇筑18个尺寸为100 mm×100 mm×100 mm 试块,成型后移入HBY-28B型水泥恒温恒湿标准养护箱中养护24 h后拆模养护28d(温度20 ℃,相对湿度95%)。
依据GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》规定的快冻法,养护28 d后将充分饱水的试件进行冻融循环试验,试件中心温度控制在-18~5 ℃(±2 ℃)范围内,每次冻融循环过程持续时间为3 h左右,在冻融过程中试件处于完全浸水状态。
每冻融循环25次(即当冻融次数N=0,25,50,75,100,125,150,175,200时)取出预埋设不透水钢环的混凝土立方体试块进行水渗透性测试,试验仪器为Autoclam渗透性测试仪。每冻融循环50次(即当冻融次数N=0,50,100,150,200时)每组任取3个未埋设不透水钢环试件进行单轴抗压强度测试,单次冻融循环过程在3 h左右完成,冻融过程中控制试件的中心温度在-18~5 ℃(±2 ℃)范围内,记录试验数据。
1.3 试验改进方法和措施
Autoclam混凝土渗透性测试仪在现场和实验室条件下均可使用,试验过程中该设备保持混凝土顶部的压力为恒定状态,并自动记录测试过程中试件的吸水量,最终得到混凝土的吸水率。为解决试件随冻融次数的增加而不断剥落等问题,本试验于混凝土试件内预埋不透水钢环,利用螺栓螺母将试件固定在仪器与底板之间以保证仪器与试件的接触稳定及密封性。
混凝土试件在冻融前,需将其充分饱和后再放置于快速冻融试验机内进行快速冻融。饱和过程通常为将养护好的试件完全浸没于水中4 d左右[14],耗时长且无法保证试件得到充分饱和。本试验利用真空泵和不锈钢耐压容器组装简易的真空饱和装置,基本方法是:设定数字压力控制表上下限,调节真空泵在低于下限值时自动工作,使耐压容器完全处于真空状态,维持12 h后打开水阀往容器内通水,使试件饱和。
2 试验结果和分析
2.1 水渗透性试验结果
不同冻融循环次数下各组试件每次水渗透性测试试验的测试时间为15 min,选取对应冻融次数下的10 min水渗透量,见表2。
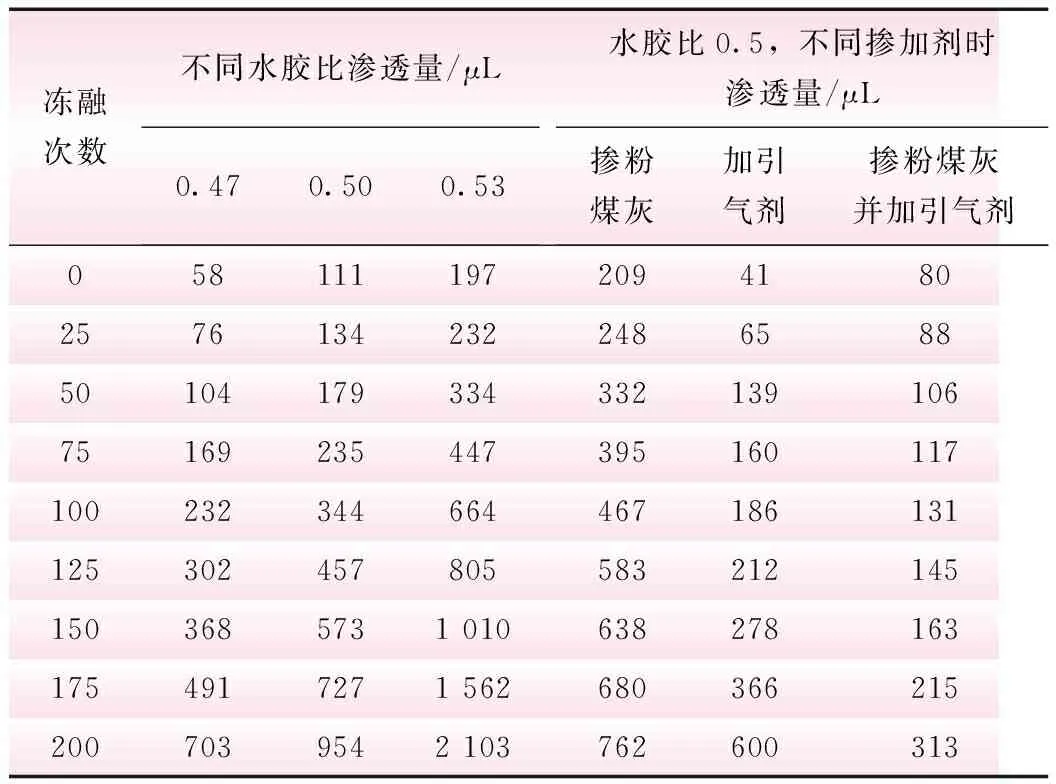
表2 混凝土试件平均水渗透量
2.2 水渗透系数的反演计算
在三维渗流有限元分析[15]的基础上,运用Seep3D构建试件1∶1三维模型,假定混凝土为材料1,不透水钢环为材料2,形状假设为六边形。按照1.0×10-10~1.0×10-6m/s输入材料1渗透系数,而材料2渗透系数设定为极小值1.0×10-14m/s,模拟钢环内部材料1的稳定渗流情况,0.5 m渗透水头截面云图见图1。渗水量与渗透系数之间的关系如图2所示,进而由实测试验渗水量内插得到相应的渗透系数。

图1 0.5 m渗透水头截面云图(单位:cm)
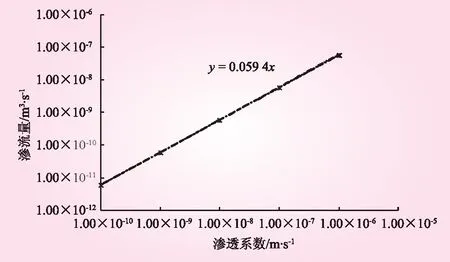
图2 渗透系数与渗流量关系
2.3 冻融作用下配合比对混凝土渗透性和抗压强度的影响
2.3.1水胶比对混凝土渗透性的影响
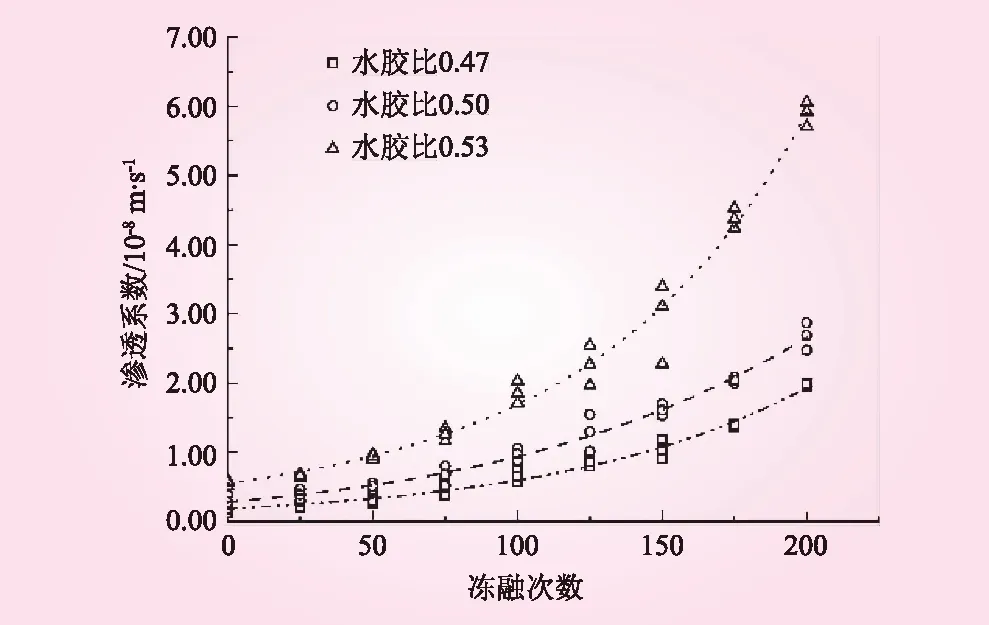
图3 3种水胶比混凝土渗透系数随冻融次数变化曲线
3种水胶比混凝土渗透系数随冻融次数变化曲线如图3所示。可以看出,水胶比为0.47、0.50、0.5的3组混凝土试件,其渗透系数随冻融次数的增加均表现为指数型式增长,经200次冻融循环后,渗透系数分别由冻融前的1.626 42×10-9、3.009 81×10-9、5.514 88×10-9m/s增加到1.971 33×10-8、2.695 75×10-8、5.898 11×10-8m/s。可见,在冻融循环作用下,相同条件下水胶比越小,混凝土的渗透性就越弱。对比水胶比0.47与0.50的渗透系数变化情况,同一冻融次数下,两者相差不是很大,说明仅采取降低水胶比的措施,对混凝土渗透性的改变不是很明显。
2.3.2粉煤灰对混凝土渗透性的影响
如图4所示,冻融循环约170次前,掺粉煤灰混凝土的渗透系数均高于不掺粉煤灰的,170次后则情况相反,且不掺粉煤灰的增长速率加快;另外,随冻融次数的增加,掺粉煤灰混凝土的渗透系数逐渐增大,增长速率先增大后减小。
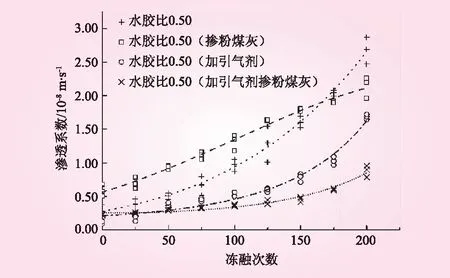
图4 水胶比0.5,不同掺加剂混凝土渗透系数随冻融次数变化曲线
2.3.3引气剂对混凝土渗透性的影响
从图4可以看出,在冻融循环150次以前,加引气剂混凝土的渗透系数增长不明显,其后,渗透系数才出现明显的增大,这表明掺引气剂能明显的改善混凝土的孔隙结构,增强其抗渗效果。进一步,在粉煤灰和引气剂双掺的情况下,冻融次数达到200次时,其渗透系数由未冻融前的2.233 99×10-9m/s增大到冻融后的8.786 41×10-9m/s,变化不是很明显。在冻融50次以前,双掺混凝土的渗透系数要大于加引气剂的,当超过75次后,双掺混凝土的渗透系数仅有略微的增长,直至冻融循环200次增加到8.786 41×10-9m/s。
3 混凝土渗透性与抗压强度的相关性分析
随着冻融次数的不断增加,试件微裂纹扩张、表面剥落等现象越来越严重,试件的抗压强度不断降低。
3.1 渗透系数与抗压强度相关性模型的提出
对冻融循环后混凝土水渗透性与抗压强度试验结果归一化处理后,相对抗压强度、相对渗透系数与冻融次数的关系如图5、6所示。从图5、6可见,相对抗压强度、相对渗透系数均随冻融次数的增加而逐渐增大。
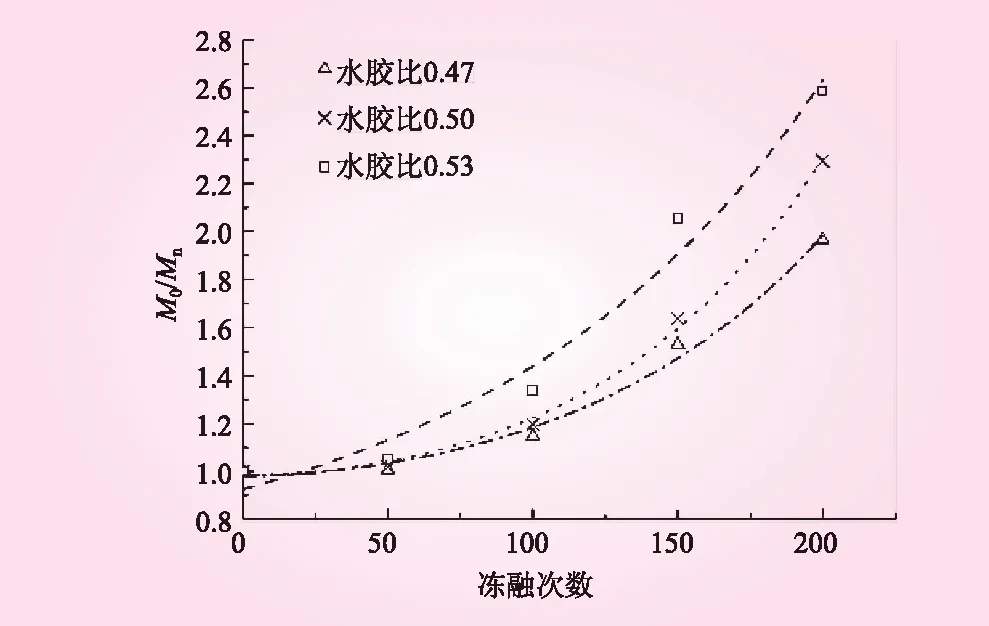
图5 相对抗压强度与冻融次数关系曲线
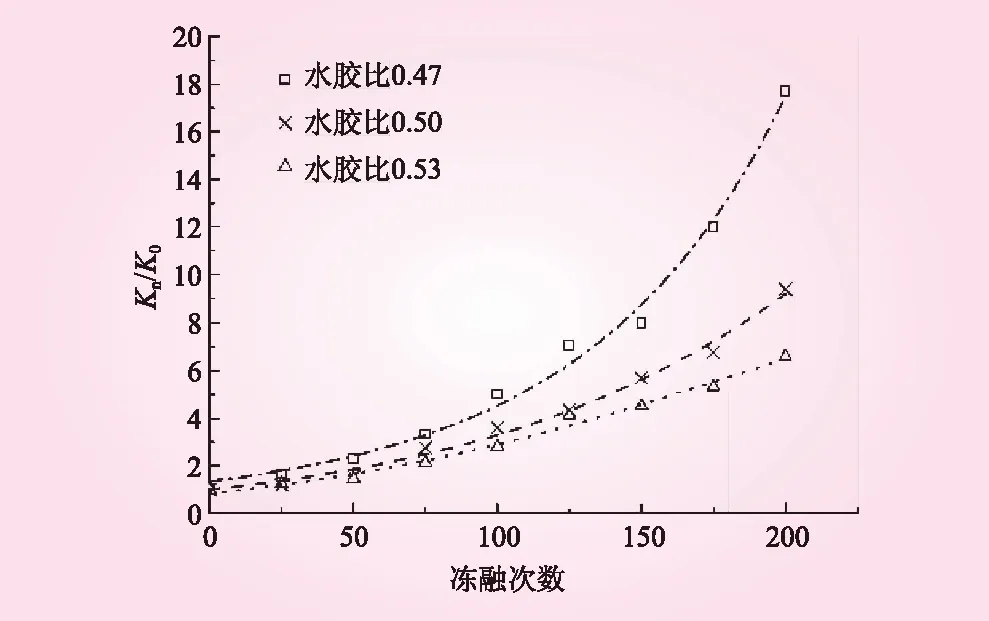
图6 相对渗透系数与冻融次数关系曲线
由图6可看出,渗透系数与冻融次数的变化存在指数关系,相关性系数分别为R2=0.984 9,R2=0.965 9,R2=0.968 5,其衰变速率dKn/dN与冻融循环的渗透系数差成正比,即
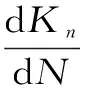
(3)
Kn=λ1K0eaN
(4)
式中,λ1为渗透系数衰变系数;Kn,K0为冻融后、未冻融前的渗透系数;a为待定系数;N为冻融循环次数。
以水胶比为0.50的混凝土试件水渗透性测试结果为基准,对试验测试所得结果进行最小二乘分析,求得渗透系数衰变系数λ1=0.983 2。则相对渗透系数与冻融循环次数的相关关系为
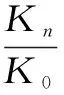
(5)
同理,相对抗压强度与冻融次数同样呈现出指数关系,即
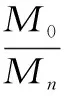
(6)
式中,λ2为衰变系数;b为待定系数;Mn,M0为冻融后和未冻融前的抗压强度。
以水胶比为0.50的混凝土试件测试结果作为基准值,对试验所得200次内冻融循环的抗压强度试验结果进行最小二乘分析,衰变系数λ2=0.876 8,相对抗压强度与冻融循环次数的相关关系为
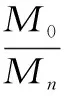
(7)
3.2 确定相关关系的修正系数
根据ω=0.47、0.50、0.53三种水胶比下的水渗透性测试结果,确定相对渗透系数与冻融次数关系的水胶比修正系数kω1=a,以ω=0.50 的试验结果为基准,对3种工况下的结果进行归一化处理。经回归计算,修正系数kω1与水胶比的关系为
kω1=0.077 3ω-0.026 1 (R2=0.97)
(8)
同理,根据3种水胶比下抗压强度试验结果,确定相对抗压强度与冻融次数关系之间的水胶比修正系数kω2=b,经回归计算得修正系数kω2与水胶比的关系为
kω2=0.032 8ω-0.012 4 (R2=0.99)
(9)
3.3 相关关系的建立
综上所述,在考虑水胶比修正情况下,由式(5)、(8)可得相对渗透系数与冻融次数的相关关系为
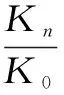
(10)
由式(7)、(9)相对抗压强度与冻融次数相关关系为
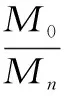
(11)
令
ρ1=Kn/K0,ρ2=Mn/M0
(12)
根据上述推导,修正后,相对渗透系数与相对抗压强度相关关系为
(13)
式中,m、n、d为3个待求参数。
根据渗透系数及抗压强度对应的试验数据,结合MATLAB最小二乘参数界定方法,结果为m=36.259 1,n=6.347 3,d=5.721 4,R2=0.968,回归均值总偏离接近1,得出的参数即为最优解,将参数代入得相对渗透系数与相对抗压强度相关关系为
ρ1=36.259 1e-6.347 3·ωρ2-5.721 4·ω
(14)
式中,ω为混凝土水胶比。
由式(14)可知,在水胶比一定的情况下,相对渗透系数与相对抗压强度之间呈现出良好的幂函数关系,将抗压强度试验数据带入式(12)、(14),计算得到的相对渗透系数与试验实测结果偏差情况如图7所示。
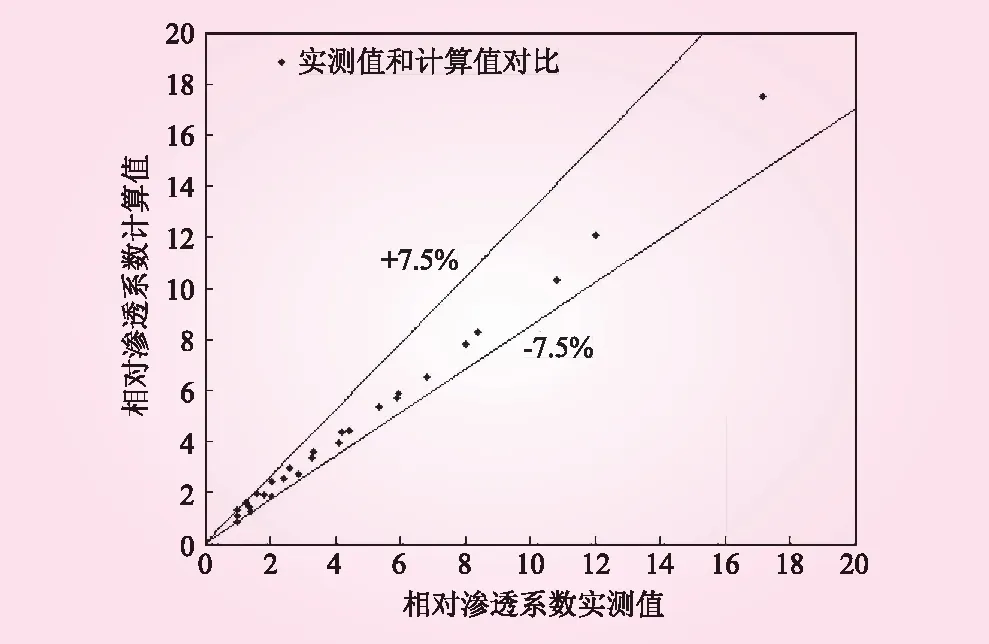
图7 相对渗透系数实测值与计算值对比
4 结 论
(1)采用Autoclam混凝土渗透性测试仪测定了冻融循环作用后流入混凝土试件的渗水量,通过真空饱和和植入圆形不透水钢环等方法,解决了试件饱和耗时长和冻融破坏造成的试件表面剥落、不平整问题。结合Seep3D软件,模拟了混凝土试件1∶1的三维渗流过程,得到了渗透系数与渗水量之间的关系,通过内插计算得到了与试验数据对应的渗透系数。
(2)随冻融循环次数的增加,混凝土的渗透系数呈现指数增长趋势,速率逐渐增大,高冻融次数下不掺外加剂混凝土的渗透系数变化幅度较为剧烈;其他条件相同情况下,水胶比越小,混凝土的抗渗性能越好;而同时掺加粉煤灰和引气剂能明显提升混凝土在整个冻融循环过程中的抗渗性。
(3)混凝土的相对渗透系数与相对抗压强度之间存在良好的相关性,本文建立了考虑水胶比修正的相对渗透系数与相对抗压强度关系,并对本试验数据进行了偏差验证,计算结果与实测结果吻合良好;在相关情况下,可以通过渗透系数推求冻融后混凝土的抗压强度。

