水工钢闸门模糊刚度可靠度进一步研究

郑鼎聪，冷 伟，周建方

(1.河海大学机电工程学院，江苏 常州 213022；2.四川省水利水电勘测设计研究院，四川 成都 610072)

0 引 言

对水工钢闸门结构进行模糊刚度可靠度分析时，由于缺乏足够的工程资料，无法通过模糊统计法及专家经验法等常见方法确定主梁相对变形模糊允许值的隶属函数。解决该问题的常见思路是依据研究对象的特点，选择常用的模糊分布形式为隶属函数。文献[1- 6]均是按照该思路将研究对象的隶属函数定为降半梯形分布。在确定降半梯形隶属函数后，问题的关键在于隶属函数的模糊上下限取值。目前，对水工钢闸门刚度可靠度进行研究的文献[3- 4]中对于模糊上下限的取值存在分歧。文献[3]主张将模糊下限值取为钢闸门设计规范[7]规定的主梁相对变形允许值，而文献[4]中的模糊下限值却小于允许值。两篇文献均未对取值的理由进行详细说明。因此，钢闸门主梁相对变形模糊允许值选用降半梯形隶属函数进行模糊刚度可靠度分析时，有必要对的模糊上下限取值进行进一步研究。

由于正态型隶属函数在工程运用中的普遍性，文献[8-9]中将研究对象的隶属函数假定为降半正态分布。为研究不同的隶属函数形式对钢闸门刚度可靠度结果的影响，本文也将计算钢闸门主梁相对变形模糊允许值隶属函数为降半正态分布时的可靠度指标，并对比两种隶属函数所得结果的差异。

1 极限状态方程的建立

由于主梁变形对闸门结构的变形起决定性作用，本文主要以主梁为例进行分析。主梁通常简化为受均布载荷的简支梁，其相对变形值为

(1)

式中，W为挠度；L为主梁跨度；q为荷载；EI为抗弯刚度。

将其改写为一般式可得

(2)

式中，S为荷载效应，S=qL2/8；C为与主梁端部约束条件、跨度有关的系数，C=384/(40L)。

根据钢闸门设计规范[7]对于变形验算的规定

f≤[f]

(3)

式中，[f]为规范规定的相对变形允许限值，露顶门为[f]=1/600、潜孔门为[f]=1/750。

由式(3)可建立闸门结构正常使用极限状态方程

[f]-f=0

(4)

在此极限状态方程中，荷载效应和抗弯刚度均在f中反映，与承载能力极限状态方程的表示不一致。为此，定义抗力R为

R=CEI[f]

(5)

将式(2)代入式(4)，并根据式(5)定义，有

R-S=0

(6)

此式与承载能力极限状态方程完全一致，可用JC法计算可靠度指标。

2 基本统计数据

2.1 荷载的统计参数

闸门结构所受荷载主要有静水压力、动水压力、波浪力和地震动水压力等。由于本文主要研究的是采用不同模糊隶属函数下的可靠度计算结果差异，为简化计算过程，只考虑闸门受静水压力的作用。露顶门与潜孔门的静水压力统计分析结果[4]如表1所示。

表1 露顶门与潜孔门的静水压力统计参数

2.2 抗力的统计参数

极限状态方程(6)式定义的抗力可改写成一般的表达式

R=KPKMKAK[f]RK

(7)

式中，RK为相对变形达到钢闸门设计规范规定标准值[f]时计算所得的抗力标准值；KP，KM，KA，K[f]分别为反映计算模式、材料性能、几何参数、[f]的不定性的随机变量。

抗力的不定性采用变量KR来描述

(8)

其平均值

μKR=μKPμKMμKAμK[f]

(9)

变异系数

(10)

由式(5)可知，材料性能指的是钢材的弹性模量，目前国内统计量为KM=1.0，δM=0.06。本文按文献[10]中有关规定对焊接工字钢截面统计参数分析的结果为KA=1.0，δA=0.022。由于主梁是受弯构件，根据文献[11]，受弯构件计算模式不定性统计参数为KP=1.0，δP=0.1。将[f]看作模糊变量(下文将规范规定的主梁相对变形允许限值表示为[f]K)，其模糊隶属函数的确定对模糊可靠度结果有较大影响。

图1 降半梯形隶属函数

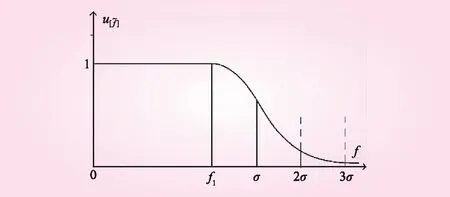
图2 降半正态型隶属函数

图1为降半梯形隶属函数图形，表达式为

(11)

图2为降半正态型隶属函数图形，表达式为

(12)

式中，f1，f2为相对变形允许值的模糊上下限值；k为待定系数。

降半正态型隶属函数需要两个已知隶属度的点确定其表达式。因此本文参照降半梯形分布中的f2，在降半正态分布中引入f2点并假定其隶属度分别为0.01、0.001、0.000 1以得到不同的k值(降半正态分布隶属度为0的点为正无穷)，计算在不同隶属度下的模糊可靠度结果并进行比较分析，以确定f2隶属度对可靠度结果的影响。

结构模糊失效域与模糊允许域互为补集，因此模糊失效域的隶属函数分别为升半梯形与升半正态型。

升半梯形隶属函数表达式为

(13)

升半正态型隶属函数表达式为

(14)

2.2.1升半梯形隶属函数对应的抗力统计参数

考虑到直接采用模糊随机事件概率模型计算可靠度时需要用到数值积分，过程较为繁琐，本文将采用当量随机化方法进行可靠度计算。参照文献[12]对模糊变量[f]进行随机化处理。当模糊隶属函数为升半梯形分布时，当量随机化后的均值和标准差分别为

(15)

为研究f1，f2变化对可靠度结果的影响，设

f1=α[f]K，f2=εf1

(16)

其中，分别取α为1，0.95，0.9，根据工程经验[13]，一般可取ε=1.05～1.3。

在确定μK[f]之后可求出K[f]为

K[f]=μK[f]/[f]K

(17)

由式(15)和(17)可得

(18)

(19)

由式(18)、(19)可知当隶属函数为升半梯形分布时，描述[f]不定性的统计参数K[f]、δK[f]的取值与[f]K无关，即与闸门类型无关，且δK[f]仅与ε有关。这是由于两类闸门所用的隶属函数形式相同，仅是起始点不同而已，即绝对值不同，而绝对值的控制是由安全系数决定的，K[f]、δK[f]与绝对值无关，且式(8)中其他参数也与闸门类型无关，所以最终统计参数就与闸门类型无关。结合式(8)、(10)、(18)及式(19)可得采用升半梯形分布时不同f1，f2取值情况下的钢闸门KR及δKR如表2，抗力分布为对数正态分布。

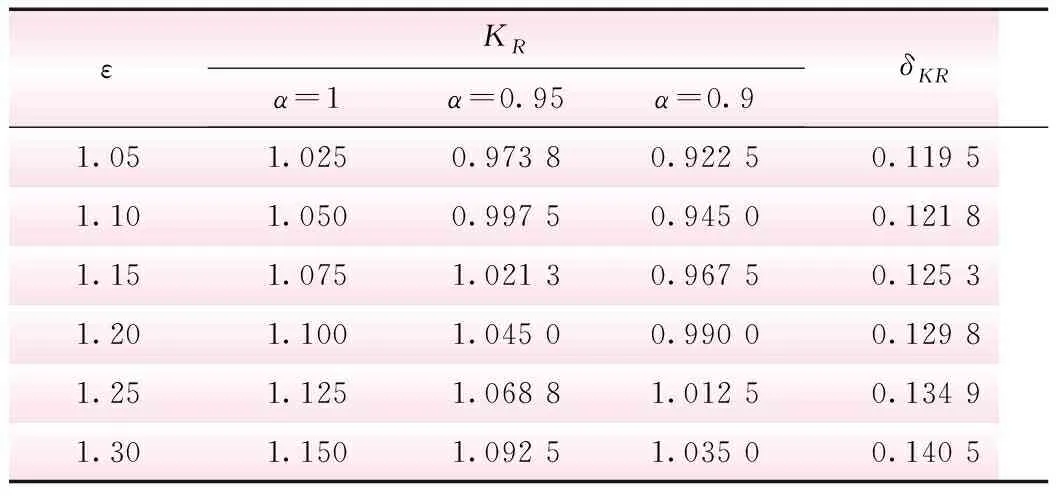
表2 升半梯形分布时α、ε不同取值情况下的钢闸门抗力统计参数

2.2.2升半正态型隶属函数对应的抗力统计参数

将升半正态分布看作概率分布函数，f1=[f]K，引入f2并假定其隶属度以确定k值。参考文献[14]中对于连续型随机变量已知分布函数求期望及方差的定理3并加以推导，可得升半正态型隶属函数当量随机化后的均值和标准差分别为

(20)

结合式(17)、(20)可得

(21)

3 模糊刚度可靠度指标计算与分析

计算模糊刚度可靠度时采用的极限状态方程为R-S=0，用JC法求得两类闸门不同隶属函数下的模糊刚度可靠度指标β见表4～7。

表3 升半正态分布 α=1时，f2不同隶属度情况下的钢闸门抗力统计参数

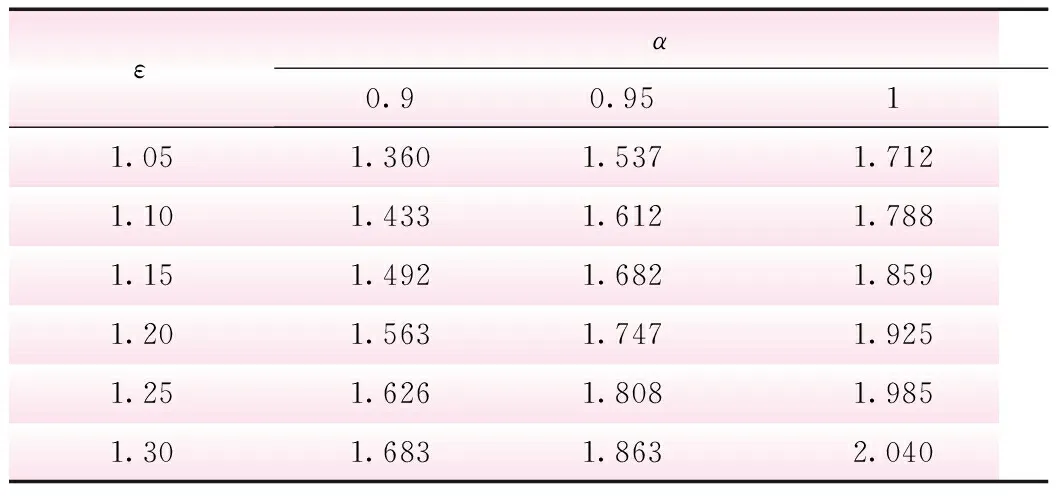
表4 露顶门升半梯形分布 α、ε不同取值情况下的可靠度指标

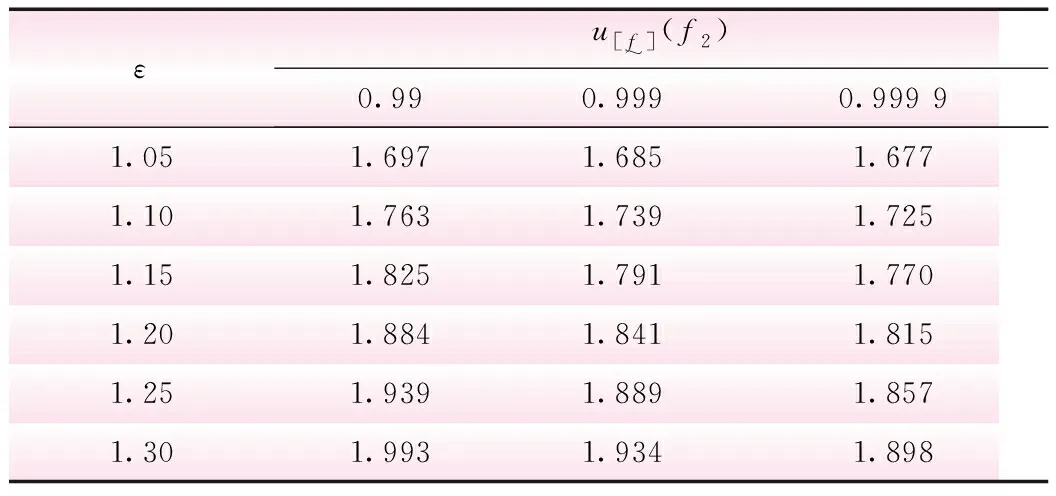
表5 露顶门升半正态分布 α=1，f2不同隶属度情况下的可靠度指标

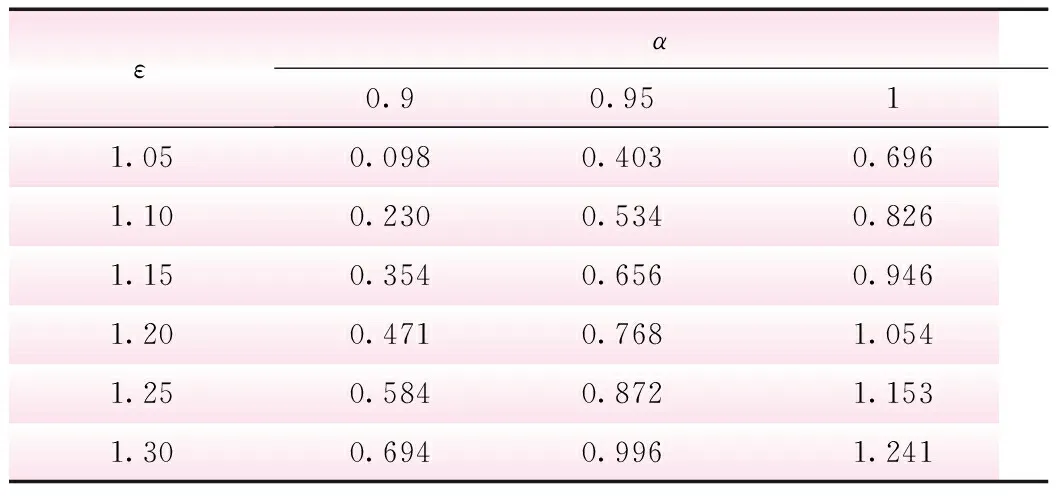
表6 潜孔门升半梯形分布 α、ε不同取值情况下的可靠度指标

表中，当α=0.9，ε=1.05时，可靠度指标仅为0.098。主要原因是在该情况下f2=0.945[f]K，即相对变形达到0.945[f]K时结构完全失效，这相当于提高了潜孔门主梁的刚度要求，因此得到较小的可靠度指标。

由表4、6可知，闸门主梁相对变形模糊允许值隶属函数选用降半梯形分布时，α与ε的取值对可靠度结果有较大影响。表6中潜孔门结构ε由1.05增大到1.10后，可靠度指标增幅较大。在未确定模糊上限真实值的情况下，出于安全性考量，应当将ε假定为1.05。表4中露顶门结构ε由1.05增大到1.10后，可靠度指标增幅较小。且由钢闸门设计规范[7]对于露顶门与潜孔门主梁相对变形允许值的规定可知，露顶门主梁较潜孔门对刚度的要求较低。同时结合安全性考虑，可将ε假定为1.10。在确定ε取值后，分析表6中α取0.9及0.95时的可靠度指标可知其数值过低，不符合实际工程要求。因此，统一将两类闸门的α定为1。

表7 潜孔门升半正态分布α=1，f2不同隶属度情况下的可靠度指标

由表5、7可知，露顶门结构f23种隶属度下的可靠度指标十分接近，而潜孔门结构可靠度指标存在一定差异。因此，出于安全性考虑，统一将钢闸门主梁相对变形模糊允许值采用降半正态隶属函数时引入的f2隶属度定为0.000 1。

将两类闸门主梁相对变形模糊允许值采用不同隶属函数时所得的可靠度指标进行对比见表8。

表8 两闸门不同隶属函数下的可靠度指标对比

由表8可知，两类钢闸门主梁相对变形模糊允许值采用不同隶属函数所得的可靠度指标差异并不显著。由于在采用降半梯形隶属函数时的计算工作量要比降半正态隶属函数小得多。因此，建议计算钢闸门模糊刚度可靠度时将主梁相对变形模糊隶属函数选为降半梯形分布。

4 结 论

(1)闸门主梁相对变形模糊允许值隶属函数选用降半梯形分布时，建议两类闸门的模糊下限都假定为钢闸门设计规范规定的主梁相对变形允许值[f]K，露顶门结构模糊上限取为1.1[f]K，潜孔门结构模糊上限为1.05[f]K。因此，文献[3]中的模糊上下限取值是正确的。

(2)闸门主梁相对变形模糊允许值隶属函数选用降半正态分布时，出于安全性考量，统一将引入的f2隶属度假定为0.000 1。

(3)由于两类闸门采用不同隶属函数计算模糊刚度可靠度所得的结果差异不显著，为降低计算工作量。建议将闸门主梁相对变形模糊允许值隶属函数选用降半梯形分布。