基于随机场理论的盾构隧道地表变形研究
孟建宇,秦拥军,谢良甫,阿卜杜海比尔·玉苏普
(新疆大学建筑工程学院, 新疆 乌鲁木齐 830047)
0 引 言
地铁隧道施工不可避免会对地层产生扰动作用,从而引起地表变形,并对城市周边环境造成重要影响,这种地表变形始终是工程建设中的重要问题。国内外众多学者[1-5]针对这一问题进行了大量研究,通过采用经验公式法[6-7]、模型试验法[8-9]和数值模拟法[10-11]得到了许多宝贵的成果。这些方法均假设土体为均质各向同性材料,认为划分为同一地层的土体性质完全相同,而忽略单一地层中土体性质的复杂性和非均质性。实际上,土体性质具有明显的随机性,同时在单一地层中又具有一定的连续性,这种复杂特点增加了地下工程建设的不确定性。考虑土体性质的随机性后,往往可以得到更切合实际的结论[12-17]。程红战等[18]分析砂土抗剪强度变异性对隧道开挖面失稳特点的影响;薛亚东等[12]计算了土体性质随机性对边坡失效概率的影响;张继周[13]在考虑土性不确定性条件下研究了基础沉降概率特征。
本文通过随机场理论,引入相关距离和变异系数来表现土体性质在一定空间内的连续性和不确定性,在考虑土体弹性模量的空间变异性基础上,结合随机分析对盾构隧道施工导致的地表变形进行了研究。
1 工程背景
乌鲁木齐地铁1号线在多个区间段施工中采用盾构法,来减小地铁隧道施工对地面建(构)筑物和交通的影响。施工主要阶段有掘进开挖、施加衬砌和注浆充填。在采用盾构机施工过程中,对土层进行开挖掘进,此时地应力部分释放,盾构机壳起到一定支撑作用,随后地应力进一步释放,拼装管片作为隧道支撑,在土体和管片接触过程中,地应力全部释放并重新达到平衡,地表变形趋于稳定。盾构法施工分析见图1。
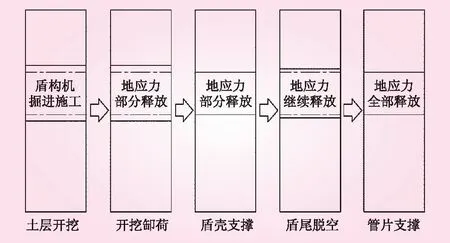
图1 盾构法施工过程分析示意
根据已有工程地质资料和施工资料,对乌鲁木齐地铁1号线某盾构区间进行建模,隧道直径取10 m,轴线埋深按18 m考虑。采用FLAC3D进行模拟,土体材料本构为摩尔-库伦,拼装管片材料本构为线弹性。本次主要分析单一地层中岩土体弹性模量空间变异性的影响,模型按单一地层计算,不同位置处土体弹性模量都不相同。模型整体尺寸取50 m×36 m,厚度为1 m。各部分材料属性见表1。表1中,null代表开挖部分的空值属性,各点弹性模量都不相同,表中给出均值。
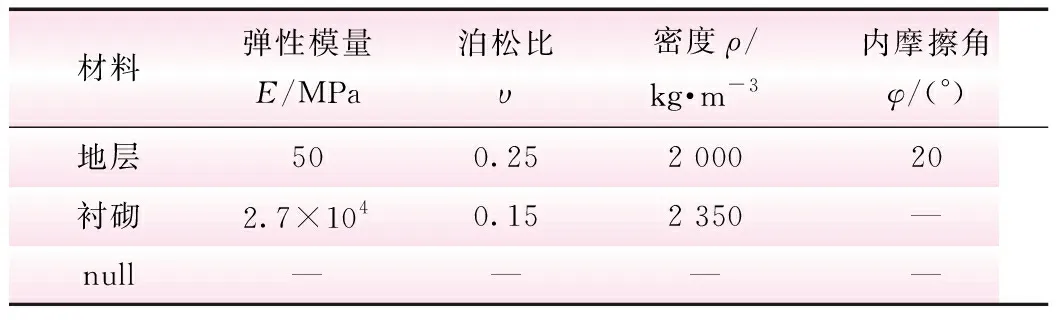
表1 模型材料属性
2 基于随机场理论的盾构隧道地表变形分析方法
2.1 随机场理论分析方法
利用随机场理论来表现土层剖面上土体弹性模量的随机性,即建立土体弹性模量随机场,用概率统计特征均值、方差等表述随机场参数。随机场理论用相关距离、自相关函数来反映土体性质在空间上的连续性,同时用变异系数反映随机性。本文采用Markov自相关函数反映地层中任意点的相关性,变异系数可以决定随机场数据概率分布形态变化。公式如下
(1)
(2)
式中,d为随机场中两点的距离;λ为相关距离;ρ(d)为自相关函数;Cv为变异系数;σ为标准方差;μ为均值。
2.2 随机场模型
此次通过协方差分解法建立弹性模量随机场模型,将FLAC3D模型单元信息代入自相关函数计算得到协方差矩阵C,矩阵C是n阶正定对称矩阵,对其做Cholesky变换,得到下式
C=XU=XXT
(3)
式中,X、U分别为下、上三角矩阵;XT为矩阵X的转置。
之后生成由n个相互独立且服从标准正态分布的随机数组成的列向量,记为Y,并进行随机场Z的一次实现,见下式
Z=XY
(4)
对Z进行数学变换得到所需的对数正态分布随机场,多次生成Y向量可生成不同的随机场。将对应弹性模量随机场一对一映射到数值计算模型中得到最终的随机场模型。盾构隧道地表变形随机性分析方法见图2。
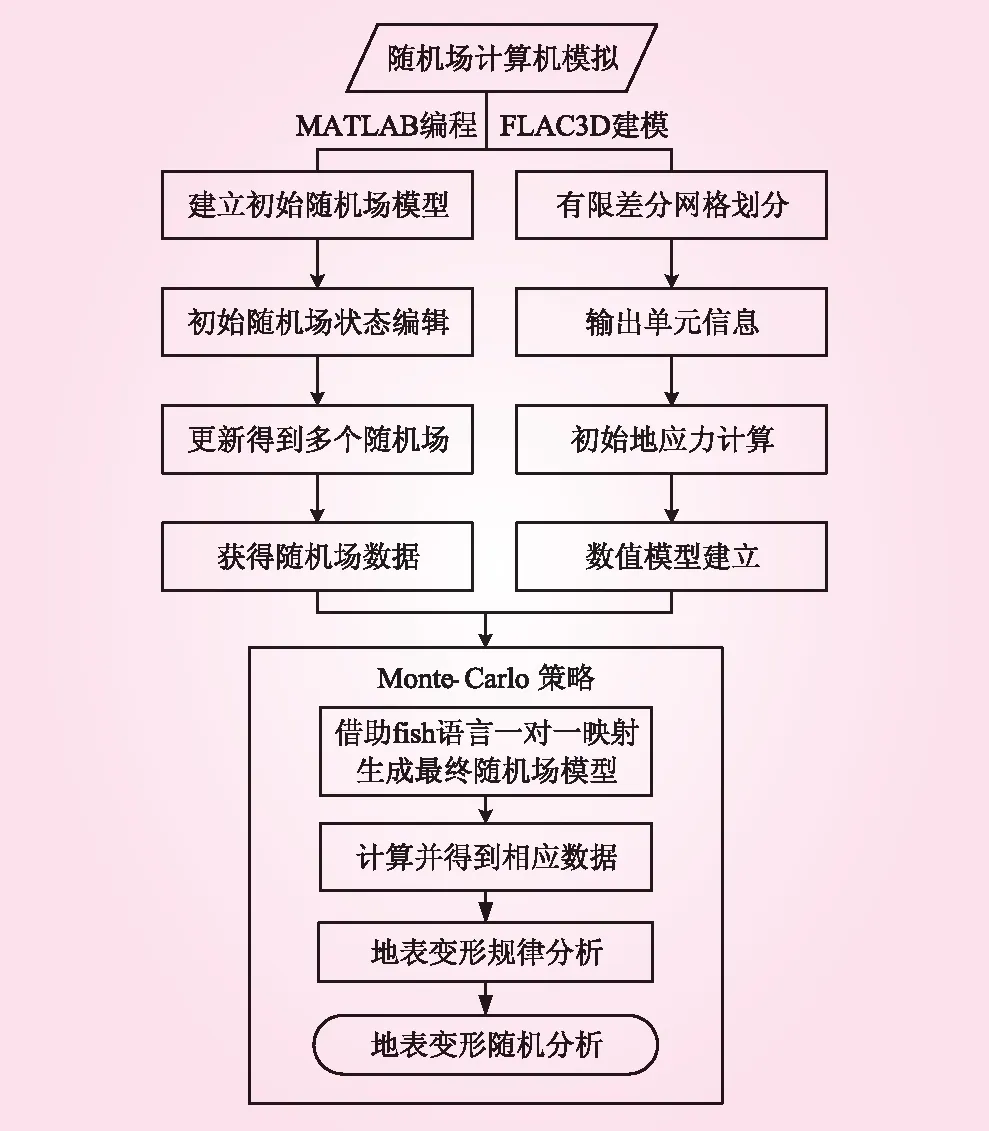
图2 盾构隧道地表变形随机性分析方法
3 地表变形确定性分析
利用建立的FLAC3D模型,在进行弹性模量随机场映射之前,按土性参数均值对地层进行赋值。目标区段隧道模型建立后,通过控制地层开挖后的地应力释放率来模拟土体与盾构机壳、管片支护接触过程。当管片拼装后,地应力全部释放,同时地层与管片支护重新达到平衡状态,此时的地表变形为最终状态。确定性分析中地表沉降见图3,图3中,虚线为隧道轴线位置。
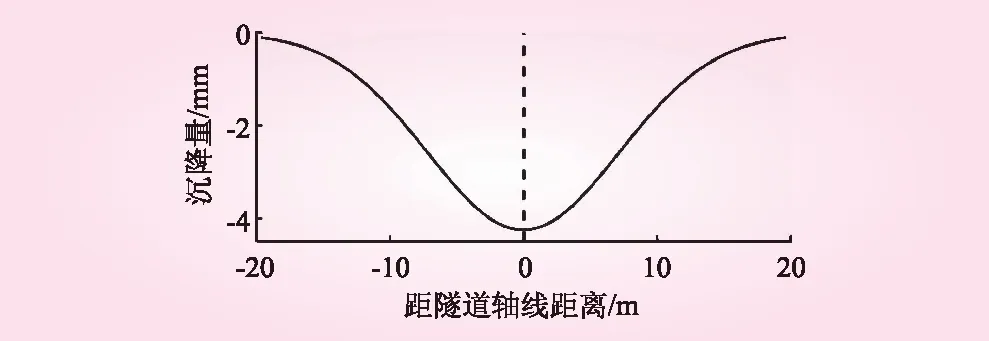
图3 确定性分析中地表沉降
从图3可知,地表变形曲线呈高斯分布,即与Peck曲线一致。同时,结合大量工程实例可以发现,隧道轴线上方土体受到扰动作用最大,沉降最大,随着向两边延伸,影响越来越小,地表变形趋近于零,即在考虑实际岩土体性质的不确定性后,Peck法反映的曲线仍是合理的。公式如下
(5)
(6)
式中,x为到隧道轴线距离;S(x)为地面沉降量;Smax为沉降量的最大值,在轴线上方;η为地层损失率;i为沉降槽宽度系数。η和i分别反映了隧道开挖对地表变形的影响程度大小和对地表水平方向影响范围的大小。
4 地表变形随机性分析
借助随机场生成方法,将弹性模量随机场映射到FLAC3D模型进行计算,模型中不同点处的弹性模量具有随机性,同时满足一定的概率分布特征,其他土性参数值为确定值。为分析相关距离和变异系数对地表变形的影响,考虑计算效率和结果准确性,设计6组试验。根据先前所做工作可知,每组计算次数取500次即可满足需要。变异系数Cv保持0.3不变,相关距离d取1、5、10 m和50 m;相关距离d保持10 m不变,变异系数取0.1、0.3和0.5。借助Monte-Carlo策略进行随机分析。
4.1 地表变形曲线随机分析
作出每组500次计算中地表变形曲线,见图4、5。图4、5中,粗实线是确定性分析中地表变形曲线,周围阴影区域由各组500次随机场计算得到的地表变形曲线组成,隧道轴线位置在图中x=0虚线处。从图4、5可知,在引入随机场后,各组试验的地表变形曲线仍满足高斯分布,曲线中间下凹、两端趋平;d=1m的地表变形曲线在确定性分析曲线周围较集中,随着相关距离的增大,曲线波动范围明显增大,即结果越来越离散;Cv=0.1时曲线在确定性结果附近非常集中,变异系数增大后结果明显趋于离散化。
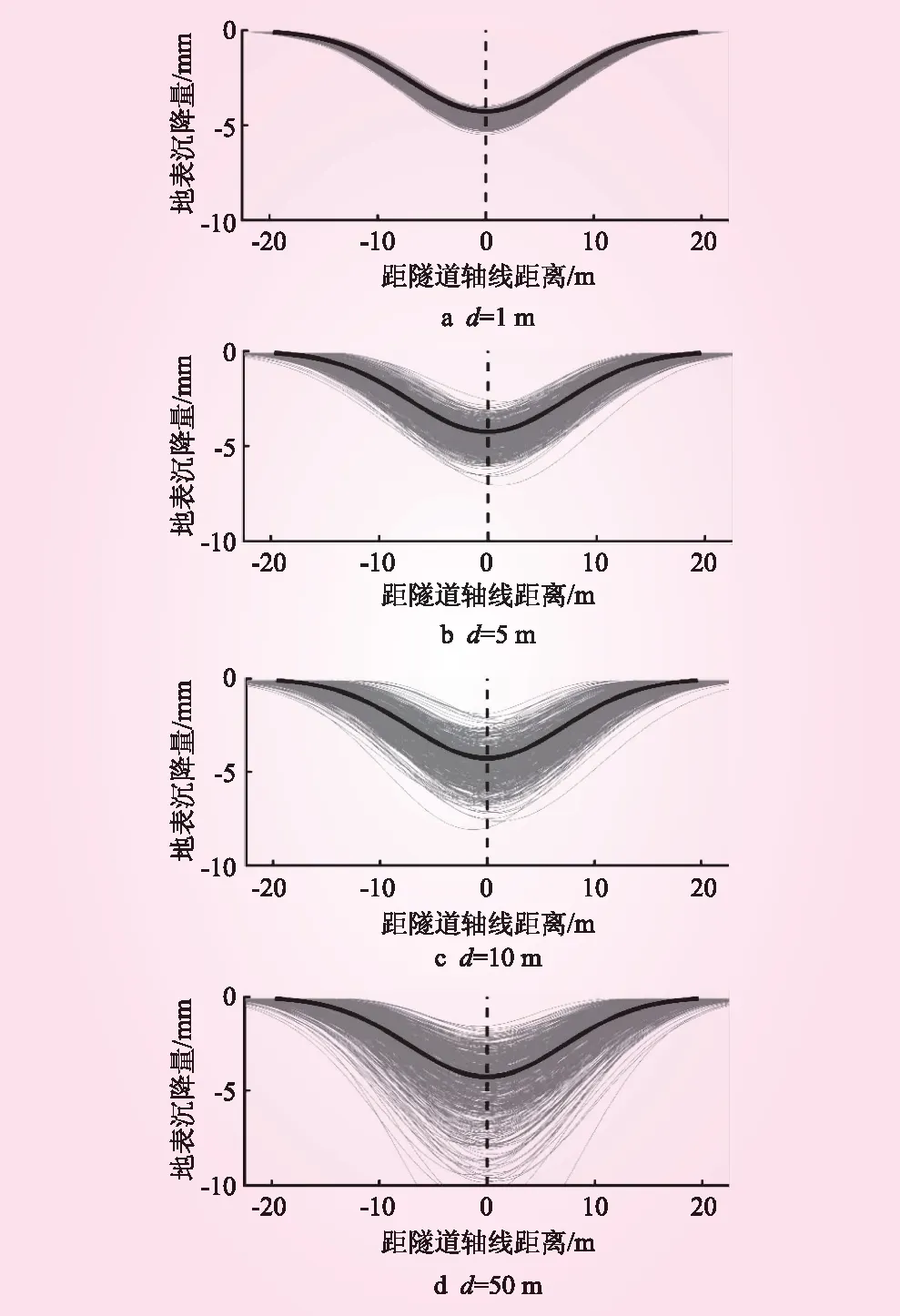
图4 Cv=0.3时的沉降槽
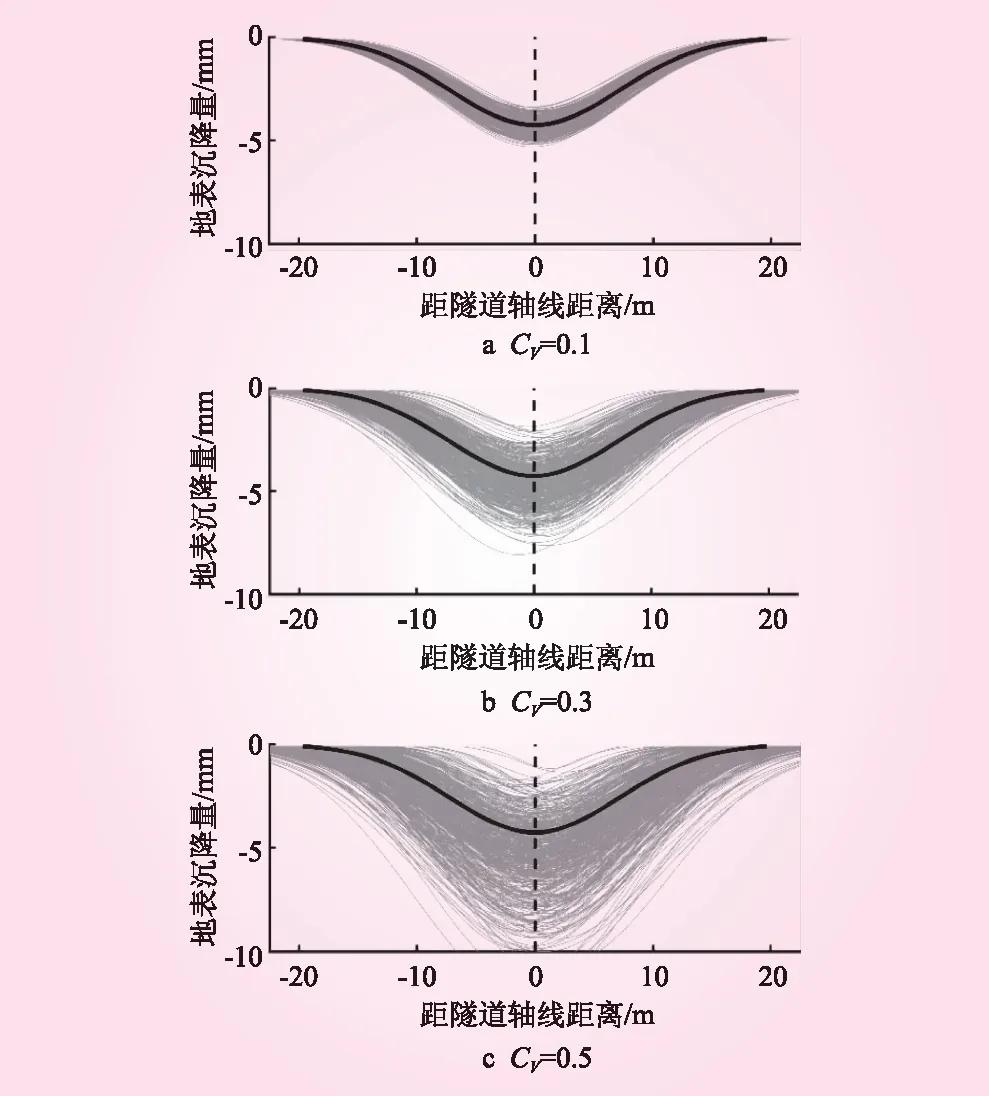
图5 d=10 m时的沉降槽
综上可知,在考虑弹性模量空间变异性后,地表变形曲线仍与Peck曲线一致,这与大量实际工程所表现的规律相符合。但也可以发现,考虑随机性后,结果具有很大的离散性,对应于地表变形影响程度、地表变形影响范围会有较大波动幅度,后续对曲线参数进行随机分析来讨论结果的离散性。
4.2 地层损失率随机分析
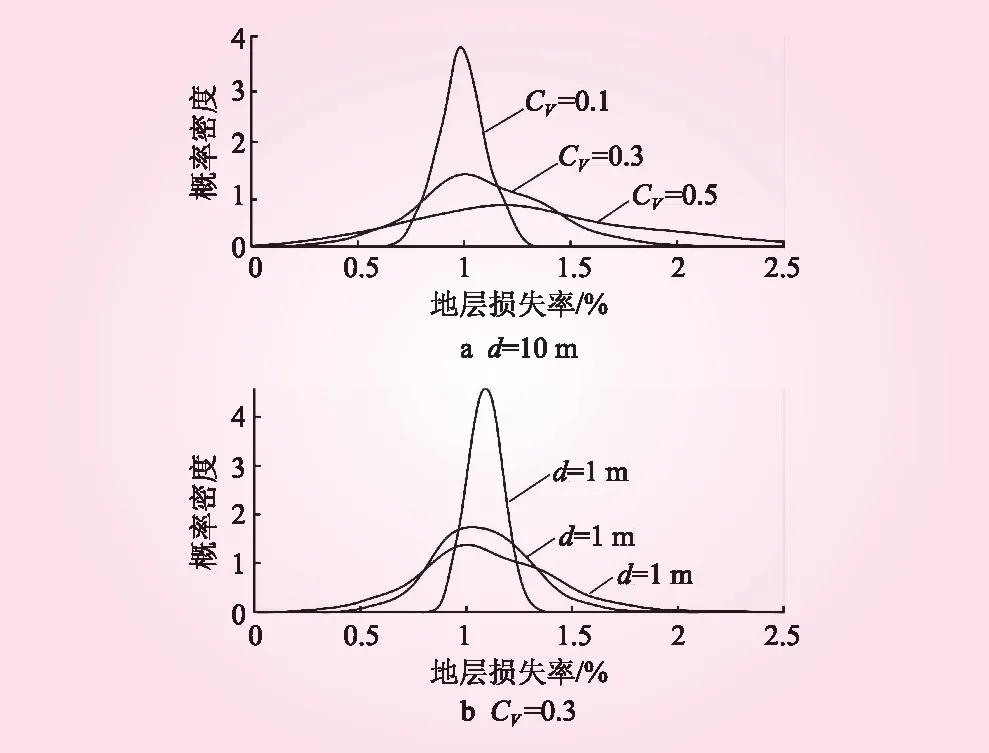
图6 地层损失率概率密度
各组随机场计算结果具有很大的离散性、不确定性。对各组结果进行概率统计分析,地层损失率的概率密度见图6。从图6可知,概率分布基本符合正态分布,中间凸、两端平,分布图越扁平代表结果离散性越大。在考虑土体弹性模量空间变异性后,地层损失率的值在一定范围内波动,分布在某个区间内的概率最大,这与传统意义上将土体看作均质材料分析得到的结果有很大不同。随机分析中可以发现,地层损失率的大值和小值相差很大,每次计算结果出现在这一区间内,而不仅仅是一个确定值或者接近一个确定值。
从图6a可知,随着变异系数的增大,概率分布越来越扁平,地层损失率分布越来越离散化,随机性越来越强。这是因为变异系数越大,土层剖面上各点弹性模量的差异性越大,极值相对于均值的差异程度会提高,同时出现概率更大,其代表高、低刚度区对地表变形程度的影响会变得更加显著,即有利方面地层损失率会变得极小,不利方面地层损失率值变得极大。从图6b可知,相关距离增大,地层损失率值变得越来越分散,这是因为单次试验中弹性模量差异在减小,但相关距离增大的试验组里,各次试验间的弹性模量差别会更加显著,这样该组试验里得到的结果离散程度更高。
4.3 沉降槽宽度系数随机分析
对各组试验里沉降槽宽度系数进行概率统计分析,结果见图7。从图7可知,概率分布基本满足正态分布,结果离散性越强,分布曲线越扁平。将地层弹性模量看作确定值得到的沉降槽宽度系数往往是一个固定值;而此次引入随机场计算,各组多次试验结果并不是一个固定值,而是在一定范围内波动,范围内小值和大值的差很大,沉降槽宽度系数随机波动的幅度不可忽略。
相关距离不变,变异系数越大,概率分布越扁平,沉降槽宽度系数的值更多的向范围内两端方向分布,这代表当土性随机性较弱时,确定性分析得到某一个区间内的固定值结果可信度较高,但随机性增强后,确定性结果的实际意义变得很小。变异系数不变,相关距离增大后,沉降槽宽度系数值的分布变得更加分散,其原因是相关距离较大试验组的各次试验间弹性模量差异增大。
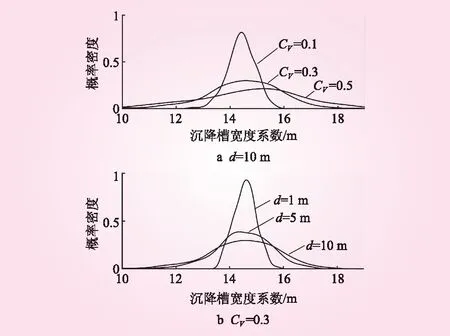
图7 沉降槽宽度系数概率密度
5 结 语
本文引入土体弹性模量随机场理论,以乌鲁木齐地铁某区间隧道开挖为工程原型,分析其对盾构隧道开挖引起的地表变形规律的影响,主要结论如下:
(1)考虑实际土体弹性模量的不确定性后,对地表变形曲线进行随机分析,曲线形态仍满足高斯分布特征,Peck法反映的规律可以用于随机场分析。
(2)土体弹性模量的不确定性对地表变形程度和范围有非常重要的影响,随着变异系数和相关距离的增大,地层损失率和沉降槽宽度系数的离散性越来越强。
(3)对随机场计算结果进行概率统计分析,地层损失率和沉降槽宽度系数的值在一定范围内波动,与确定性结果相比,波动幅度不可忽略。

