巧用生活情境原始问题 培养学生科学论证能力

卞志荣 焦建生

(江苏省天一中学，江苏 无锡 214101)

科学思维是物理核心素养的重要组成部分.其主要包括模型建构、科学推理、科学论证、质疑创新等要素.科学论证是一种基于科学知识、证据和推理以证实、辨明主张的实践活动.科学论证能力是通过论证活动表现出来的一种复杂的综合能力.要提高学生科学论证培养的实效性，教师必须依据科学理论设计高质量的学生活动.当前科学教育中开展论证活动中最重要的理论基础是图尔敏论证模式，由主张、资料、正当理由、支援、限定和反驳等6个功能要素构成的过程性模式，开启了论证逻辑的实践转向.

由于生活类情境原始问题强调的是基于学生生活实际的真实情境，来源于学生生活实际，学生具备了一定的感性认识，能引起学生学习兴趣，激发学生的探究热情，当然有利于培养学生的科学论证能力.依据图尔敏论证模式，在学生学过“超重与失重”之后，我们创设了以商场内电子台秤为背景的系列探究活动，有意识地对学生进行科学论证能力培养.

1 创设生活情境问题，培养学生科学论证习惯

教师在为学生创造科学论证机会之前，用PPT明确告诉学生，科学论证应包括提出自己的观点、提供与观点相关的证据、联系观点和证据的推理过程以及反驳等流程.教师也可以通过具体情境问题的论证解决加以示范指导，包括论证方法的选用和证据的使用等，让学生掌握科学论证的规律，在具体问题中加强科学论证过程的严密性培养，养成良好的论证习惯.

台秤是生活中常见的用具，学生在大大小小商场司空见惯.笔者就以台秤称量重物为情景设计了学生探究活动，为学生提供科学论证机会，在论证中提高思维能力，同时强化超失重概念的学习.

问题1.如图1(甲)所示，台秤上放有盛满水的有机玻璃水杯，杯底用细线系一乒乓球，试论证细线被剪断后，台秤示数与未断前有何变化？

猜想：绝大多数学生认为“示数变大”.

论证：剪断细线后，图1(甲)中乒乓球加速上升，处于超重，所以台秤示数变大；

实证：教师用课前准备好的实验器材进行演示实验，实验装置如图1(乙)所示.电子台秤规格：SF- 400，5000 g×1 g，有机玻璃筒上内径10 cm、下内径8 cm、高30 cm，乒乓球加悬线质量2 g，悬线下端系一小螺帽，隔着瓶底用强磁铁吸住螺帽.为了方便手移走磁铁释放乒乓球，用三脚架撑起玻璃筒一起放在台秤上.移走磁铁释放乒乓球使其上浮，观察球上浮过程台秤示数变化.本次实验上浮前台秤示数1580 g，上浮时示数为1571 g，台秤示数变小.与学生的猜想不一致，产生认知冲突.

(甲)

(乙)
图1

再论证：在教师的引导下，学生经过一番讨论，终于找到了正确科学的论证方法：乒乓球加速上升的同时有同样体积的水球以同样的加速度下降，乒乓球处于超重而水球处于失重，因同体积水球质量大于乒乓球质量，所以失重大于超重，综合起来系统处于失重，所以台秤示数变小，而不是变大.

问题2.如图2(甲)所示，台秤上放有盛满水的有机玻璃水杯，小铁球(直径2.5 cm)悬挂在固定于台秤上的支架上且浸没在水中，不计水的阻力，试论证细线被剪断后，台秤示数与未断前有何变化？

观点：台秤示数变小.

论证：支架、铁球及线、水和杯构成一个整体，烧断细线前台秤测得是它们的总重量，烧断细线后铁球所受重力大于浮力，向下加速下降，处于失重状态，所以台秤示数变小.

实证：实验装置如图2(乙)所示，将小球悬挂在铁架台上，将直径2.5 cm的铁球用细线悬挂在铁架台上，为了防止铁球下落砸坏水杯，在杯底垫上海绵，整个装置一起放在台秤上，细线烧断前台秤示数为3441 g，烧断后台秤示数为3423 g，确实减小，证明了学生论证的正确性.

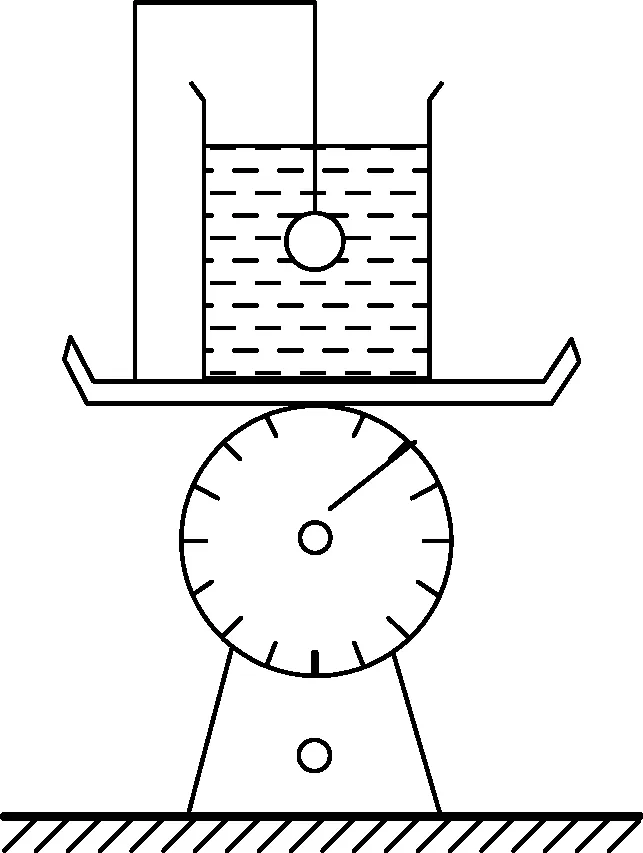
(甲)

(乙)
图2

总结：要判断台秤示数变化就是判断水杯对台秤的压力变化.大部分学生能很快建立起超失重模型，定性分析论证，比较快捷地得出结论.说明这部分学生对这个问题具备了一定的科学论证能力.少数学生采用最常规方法：通过受力分析再用牛顿第二定律列方程进行定量论证，往往卡在球与水、水与杯的作用力问题上而裹足不前.这说明论证方法的优劣会影响论证过程的快捷、准确程度.还有部分学生对图中情境缺乏全面考虑致使论证结论出现差错.所以，论证过程必须严谨，论证材料必须全面、科学.从这里我们还可以体会到论证方法的多样性，如理论论证中的定性、定量论证；事实论证中的实验论证等.以后我们还会遇到比较论证、因果论证等方法.为了检验学生论证习惯和能力以及论证方法的灵活性，笔者又提供了情境相似但有变化的问题，让学生再论证，优化论证方法.

问题3.如图3(甲)所示，将小铁球悬挂在铁架台上且浸没在水中，烧断细线后，在小球向下运动过程中台秤的示数与剪断前相比变大还是变小？

猜想：大部分学生观察不够细致，认为与问题2一样，台秤示数变小.

引导：引导学生观察情境问题3与问题2中悬挂铁球的方式有何不同？(问题3中小铁球是悬挂在台秤以外，而问题2中小铁球是悬挂在台秤上)，情境不同，当然不能盲目套用2中的论证方法，怎么办呢？让学生分组讨论后得出，必须巧选研究对象，用定量论证的方法才能解决.

(甲)

(乙)

(丙)

图3

论证：因为小球悬挂在台秤以外，悬线烧断前，要研究台秤受到的压力，必须以水和杯为研究对象.设水和水杯总重为G，铁球质量m铁，受到水的浮力为F浮，受力分析可知，台秤示数N=G+F浮.烧断悬线后，设铁球向下加速度大小为a，同体积的水球向上加速度大小也为a，要研究台秤受到的压力，隔离水和水杯，应用牛顿第二定律得到N′-G-F浮=m水球a.所以N′=G+F浮+m水球a，显然大于N，所以台秤示数比剪断前要大.

实证：实验装置如图3(乙)所示，细线烧断前台秤示数2127 g，烧断后示数为2183 g.

2 精选生活情境问题，让学生体验科学论证过程

教师可以在课堂中提出一些生活中的开放性问题来引发学生讨论、思考，充分让学生陈述自己的观点和想法，并根据学生的回答进行追问，如“你为什么这么想”、“你是怎么得到这个结论的”. 当学生遇到困难时，教师通过搭建“脚手架”帮助学生探究原认知中的不足之处，使学生重新构建正确的推理过程.这样在生生、师生互动中，让学生对彼此的观点和推理过程进行相互评判，指出各自推理过程中可能存在的疑惑或自相矛盾的地方，激发学生再次审视问题中的条件和信息，反思自己的观点，争取用更多的证据来改正或支持自己的观点.从而认识原始论证过程和科学论证过程之间的差异，促进学生逐步走上科学论证的新台阶.

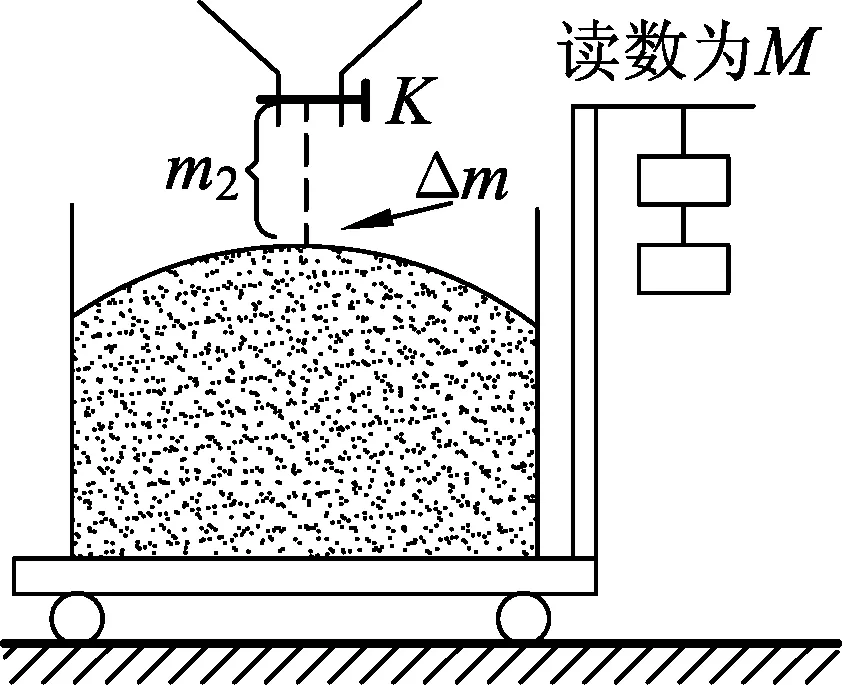
图4

问题4.自动称米机已被许多大粮店广泛使用，原理图如图4所示.买者认为：因为米流落到容器中时有向下的冲力而不划算；卖者则认为：当预定米的质量数满足时，自动装置即刻切断米流时，此刻尚有一些米仍在空中，这些米是多给买者的，因而双方争执起来，究竞哪方说得对呢？

观点：问题抛出之初，学生中存在3种观点：

(1) 同意买者观点，认为买者说得有道理.

(2) 同意卖者观点，认为卖者说得有道理.

(3) 认为买者观点和卖者观点都不对，应该是准确的，否则还有谁用这种秤呢？

引导：这是一道原始物理问题，读完题目买卖双方说的似乎都有道理，但又无法说清为什么，即论证理由不充分或论证方法找不到.但我们至少应该坚信的是：这是一道力学问题，解决力学问题首先得确定研究对象，进行受力分析.遇到这种较为复杂的原始问题，我们应该冷静下来进行理性思考，猜想此问题可能会用到什么物理知识和规律，联想、类比曾经遇到过的类似问题，或许能很快找到论证的方法.

我们是否可以这样思考：

(1) 台秤的读数是物体对秤盘的压力；

(2) 米是固体，但米流和流体相似；

(3) 处理流体问题常常要建立柱状模型，如水力采煤求水对煤层的冲力；风力发电求风对叶片的作用力等；

(4) 求变化的物理量的常用方法是微元法.

论证：设米流的流量为d，它是恒定的，自动装置能即刻在出口处切断米流，米流在出口处速度很小可视为0.若切断米流后，盛米容器中静止的那部分米的质量为m1，空中还在下落的米质量为m2，取已静止米堆m1上方在空中的一小部分米柱Δm为研究对象，经过Δt(Δt→0)时间落至米堆内，则Δm=d·Δt.设其落到米堆上之前的速度为v，其受到重力Δmg和已静止米对它的作用力F的作用，经Δt由速度v变为静止.由动量定理得

(F-Δmg)Δt=Δmv，即F=dv+dgΔt.

设米从出口处落到米表面所用的时间为t，由于m2=d·t，v=gt(阻力不计)，所以，d·v=m2·g，即F=m2g+Δmg.根据牛顿第三定律知F=F′，所以，称米机读数应为

结论：由以上定量论证可见，称米机读数包含了静止在袋中的部分m1，也包含了尚在空中的下落的米流m2，还包含了刚落至米堆上的一小部分Δm，即自动称米机是准确的，不存在谁划算不划算的问题.

总结：运用物理知识解决实际生活问题，必须把实际问题转化为物理模型和物理过程，依据所学知识和思维方法进行分析推理，建立不同物理量间的联系是科学论证中的关键所在.论证能力的提高需要在实践中不断体验、感悟.

3 活用生活情境化试题，提升学生科学论证能力

情境化试题是指以自然界及社会生活、生产中客观存在的物理现象或过程为背景，考查学习者对物理概念、规律的理解与应用能力的试题.论证解决这类试题的基本流程如图5所示.

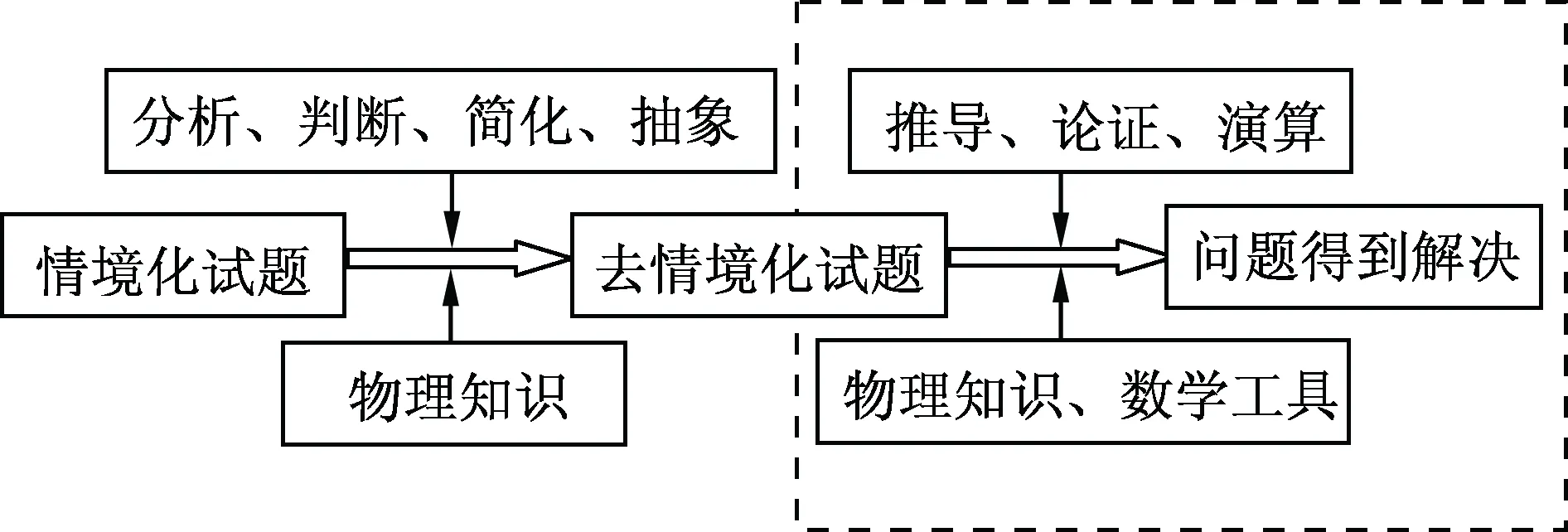
图5

新课程《标准》中明确指出，在教学设计和教学实施过程中要重视情境的创设.试题的情境要具有一定的问题性、真实性、探究性或开放性.设问的角度及方式要科学、可信、新颖、灵活.要求通过学生在应对复杂现实情境，参与相应探究学习活动中的外在表现来考查物理学科核心素养，在解决具体问题中体现和提升物理科学论证能力.

近年来，情境化试题在高考等选拔考试中也得到重视和应用.如国外流行的基于问题学习模式(PBL)等都非常强调把学习内容“嵌套”在实际问题中或真实的社会情境中；国际大型测评项目PISA，在其考试中主要使用此类试题.我们在运动学学习之后呈现给学生的情境问题是来自伊朗物理竞赛预赛试题.

问题5.打开水龙头，水就流下来，为什么连续的水流柱的直径在流下过程中减小？假设水龙头开口直径为1 cm，安装在75 cm高处.如果水在出口处的速度为1 m/s，求水流柱落到地面处的直径有多大？(不计空气阻力，g=10 m/s2)

观察：试题呈现出来后，学生也觉得题中所叙情境是生活中很常见，但好多学生一筹莫展，迟迟不能下手.究其原因反映出现在的好多学生在生活中不善于观察和思考，就连越流越细也没有印象，遇到来自身边的实际问题也不能顺利地将所学知识迁移到情境之中而得到解决.

引导：就试题本身来说，第一问属于原始物理问题，第二问进行了赋值变成了物理习题.要找到解决问题的办法，必须结合题目叙述的情景进行以下逻辑推理，方能找到论证方法.

(1) 研究对象是水.

(2) 水流做的是什么运动？

(3) 下面的水与上面的水的运动有什么不同？

(4) 上、下水流流速相同吗？

(5) 什么是它们联系的纽带？

通过以上几个“为什么”，就不难发现：水不管在什么高度，通过某一水平截面相同的时间内流过的水的体积(或质量) 相同，同时由于水在不同高度速度不等，需要用“微元法”化变为不变，建立Δt(Δt→0)时间内的柱状模型.

论证： (1) 在时间t内，流过任一水柱截面的水的体积是一定的，由于水柱顶点的水速小于下面部分的水速，故水柱的直径上面比下面大.

教师总结：该题属于联系实际的创新题，既不超出考纲要求，又能很好地考查学生分析解决实际问题的能力.同时我们又从以上论证中感悟到：解题的过程就是运用归纳推理将文字信息转化为问题情境，然后运用演绎推理将情境转化为物理条件，再选择物理规律和方法进行科学论证的过程，在问题解决中实现论证能力的提升.

通过以上系列情境问题的论证教学之后，学生不仅掌握了科学论证过程和方法，论证能力也得到了一定程度的提升.学生在论证过程中感悟到了物理问题来自于生活，学习物理知识又可以服务于生活的哲学道理，真正理解到“物理即生活”的精神内涵.在平时教学中，教师要加强STSE教学，引导学生善于观察生活，了解社会，关注科技，善于发问，敢于质疑，将所学知识和能力迁移到实际问题中，做到学以致用.教师要为学生多提供生活类情境问题，进行科学论证训练，在训练中发展学生的思维能力，提升科学素养.