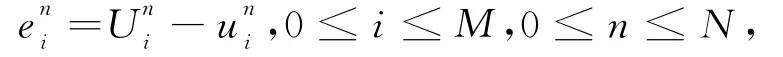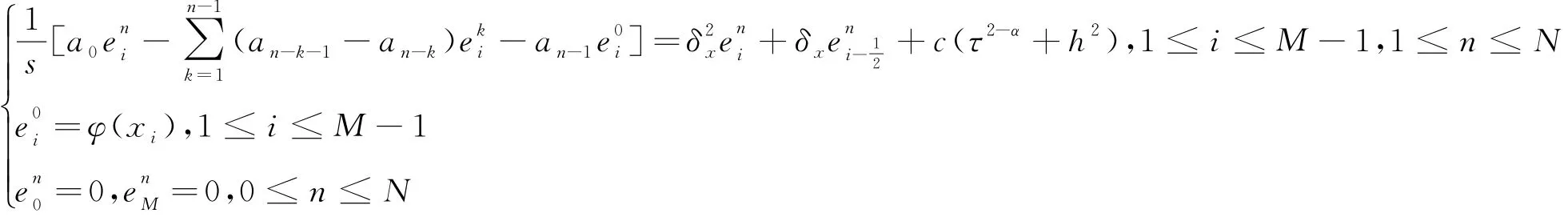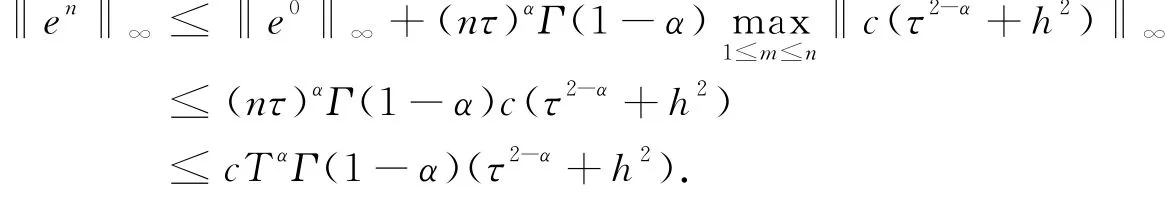一类时间分数阶扩散方程及其差分问题的研究*
汪庆康
(广西师范大学 数学与统计学院,广西 桂林 541006)
0 引言
微分方程近来受到了数学和相关学科的高度关注,广泛地应用于物理学、通信工程等领域,然而一般分数阶偏微分方程的理论研究并没有达到完全成熟的阶段.在文[2]中研究了具有时间分数阶扩散波动方程
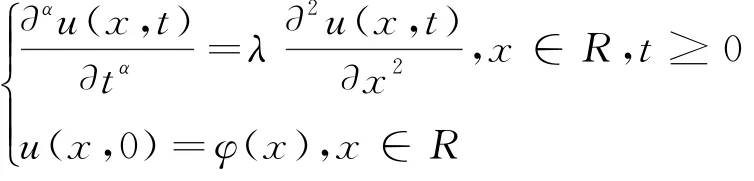
的Cauchy问题及其相关性质.
与分数阶微分方程理论方面的大量工作相比,关于它数值分析的研究还是很少的,Sanz-Serna在文[3]中提出了一种时间半离散算法,并证明了一阶收敛性;在文[4]中研究了方程
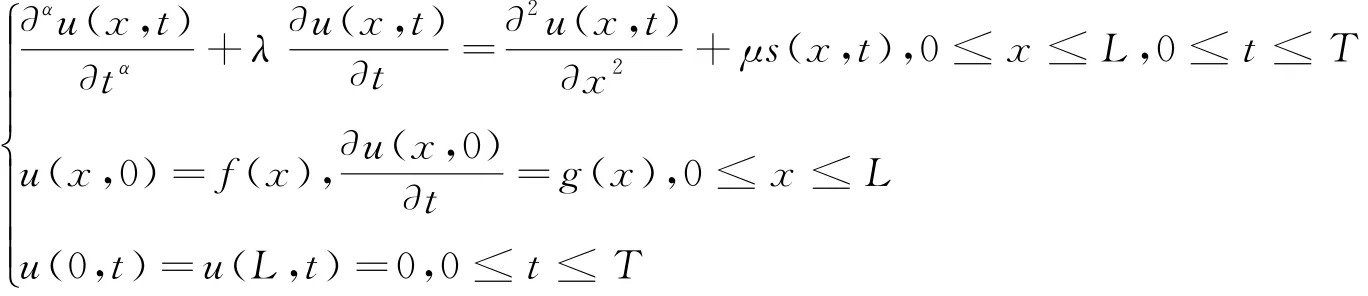
的差分形式及其相关性质.
本文首先研究了方程
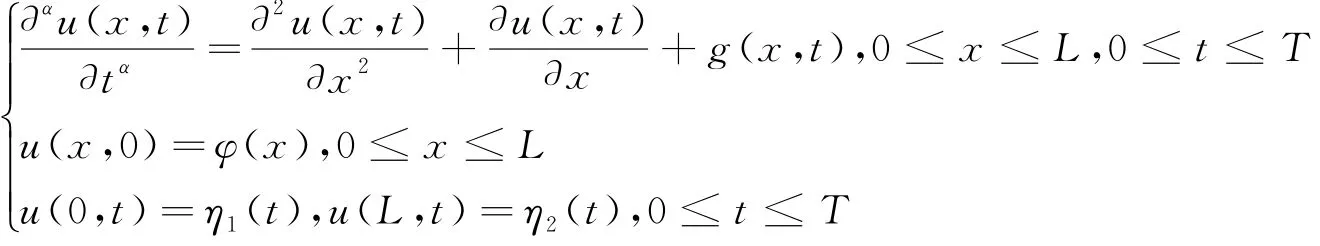
初边值问题的解,通过利用变量分离法将其转化为另一种形式的微分方程,再利用Yurii Luchko和Rudolf Gorenflo在文[1]中的定理得出原方程的解.然后在已有知识的基础上将微分方程差分化,研究了差分形式的唯一可解性、稳定性和收敛性.
1 预备知识
本节主要介绍相关的概念及其解决后续问题所需的定理.
定义1[1]设α∈ℝ,在L1[a,b]上定义α阶分数阶Remann-Liouvlie积分算子,表示成
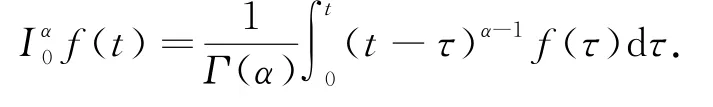
定义2[6]设α∈ℝ+,函数f(x)定义在[a,b]上,n是大于等于α的最小整数,则α阶Caputo分数阶导数定义为
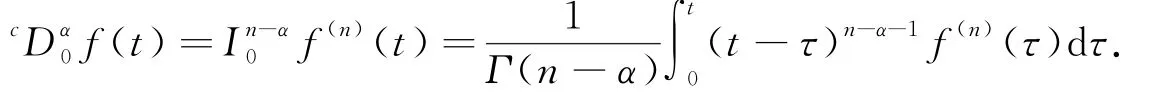
定义3[1]函数f(x),x>0,若存在实数p>α,α∈ℝ,使得
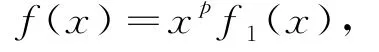
且f1(x)∈C([0,+∞)),则有f(x)∈Cα.
定义4[1]函数f(x),x>0,f(x)∈Cmα,当且仅当f(m)(x)∈Cα.
定义5[7]多参数Mittag-Leffler函数定义为
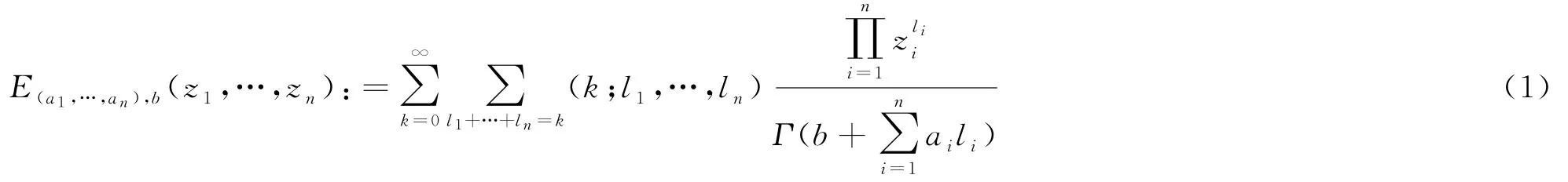
其中系数
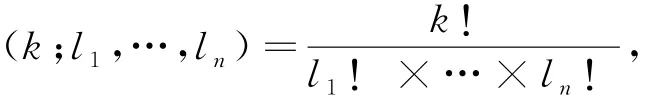
特别地,当n=1时
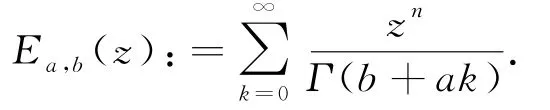
定理1[1]设μ>μ1> … >μi≥0,mi-1<μi≤mi,mi∈ ℕ0=ℕ ∪ {0},λi∈ ℝ,i=1,…,n.初值问题
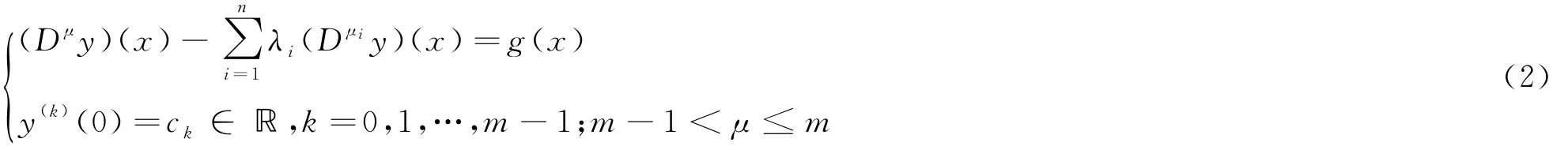
其中当μ∈ ℕ,g∈C-1,当μ∉ ℕ,g∈.则未知函数y(x)在中有唯一的解,其形为

其中

是问题(2)具有零初值条件的解,且
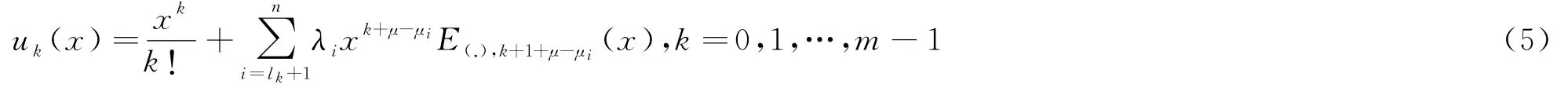

由定义5中(1)式给出.
其中lk,k=0,1,…,m-1由以下条件确定
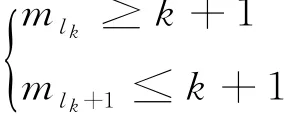
如果mi≤k,i=1,…,m-1,则lk:=0;如果mi≥k+1,i=1,…,m-1,则lk:=n.
2 分数阶扩散方程的求解
本节主要研究如下分数阶扩散方程的初边值问题,其中0<α<1.
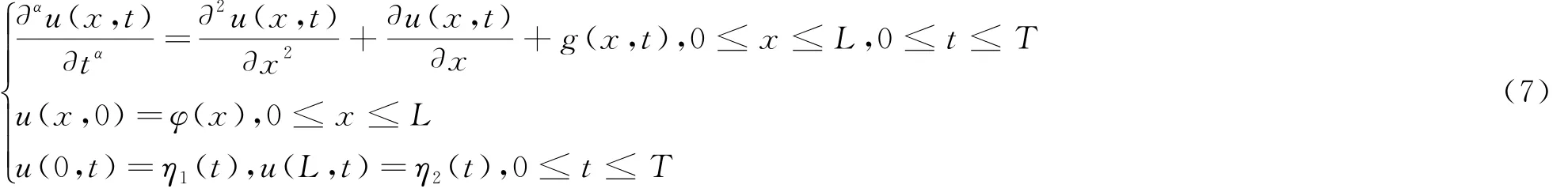
为了求非齐次边界问题(7)的解,我们令

其中w(x,t)满足

v(x,t)具有如下表达
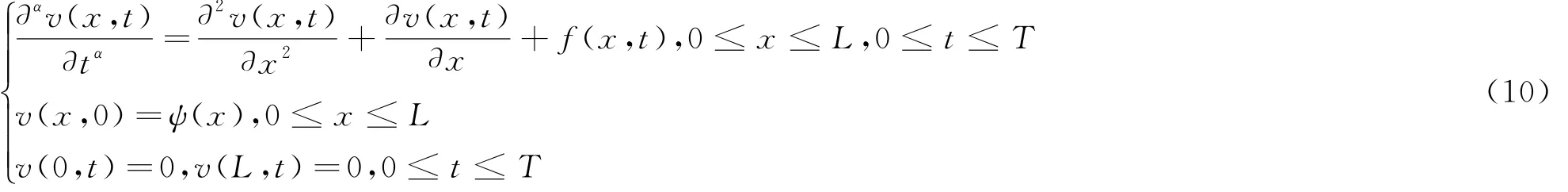
其中
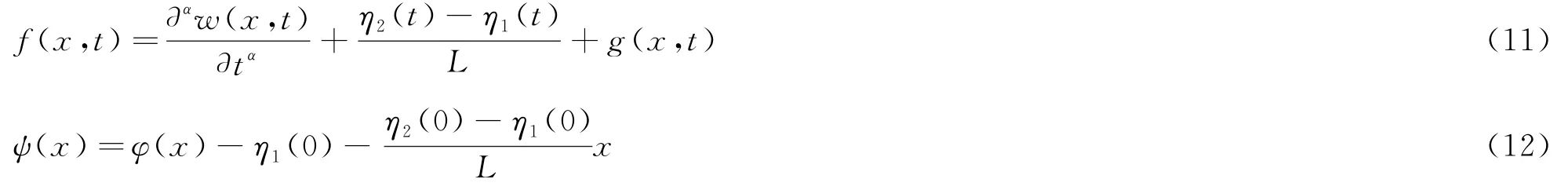
用分离变量法求齐次方程(10)的解(f(x,t)=0时),设v(x,t)=X(x)T(t)满足方程,我们可以得到微分方程

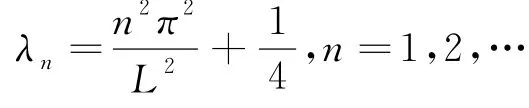
对应特征函数为
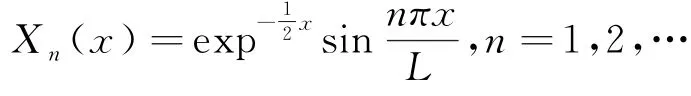
假设非齐次方程的解是

为了确定Bn(t),我们设级数(14)是可逐项微分的,将exp12xf(x,t)按特征函数展开成Fourier级数

则有

将(14),(17)带入方程(10)可得
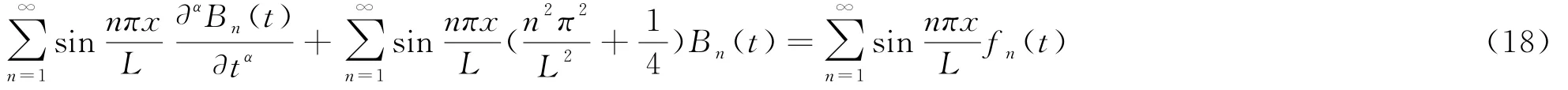
即

同时v(x,t)满足初始条件,我们有

于是

对于任意的n(n=1,2,…),(19)和(21)构成一个分数阶微分方程的初值问题,由定理1可知方程的解为
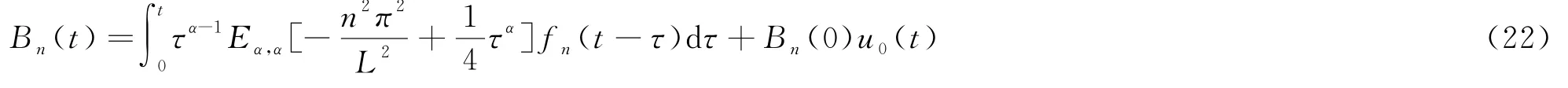
其中

则(10)式的解为
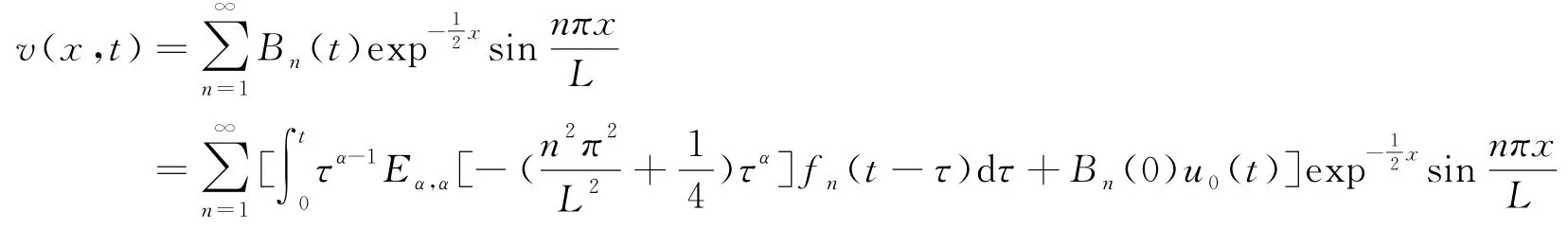
于是(7)式的解是
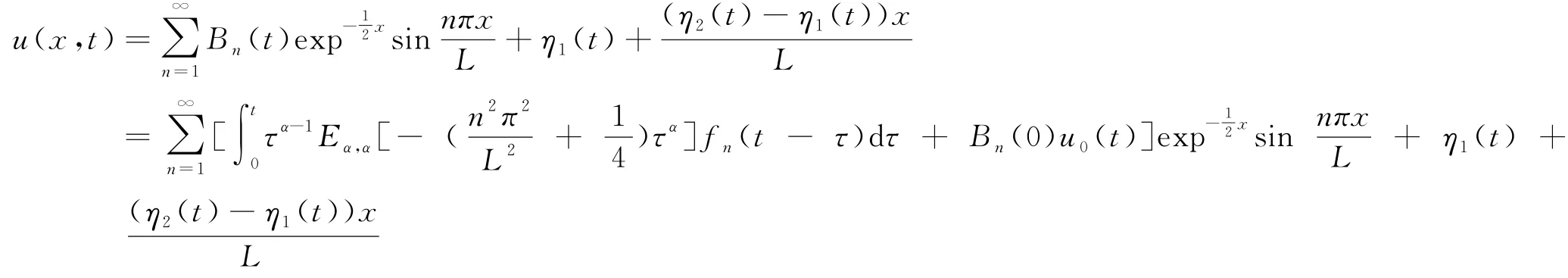
3 分数阶扩散方程的差分形式
本节主要将方程(7)转化为差分形式,研究其数值解的相关性质.
3.1 差分形式的建立
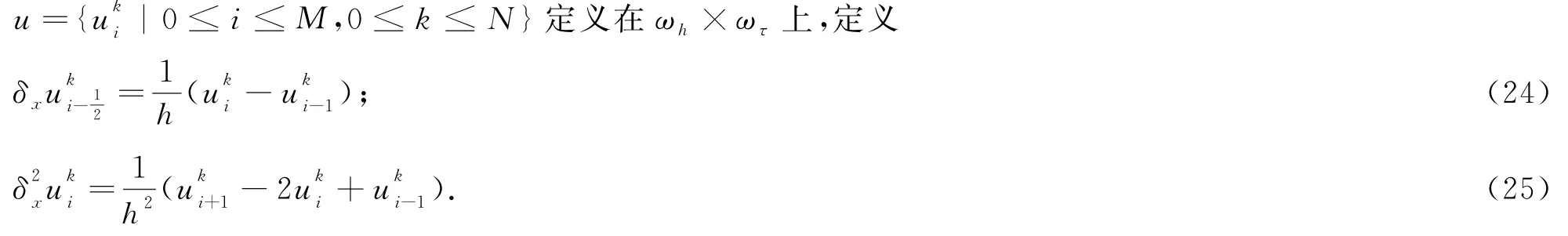
引理1[4,8]设u(x,t)∈C4,2([0,L]×[0,T]),则有
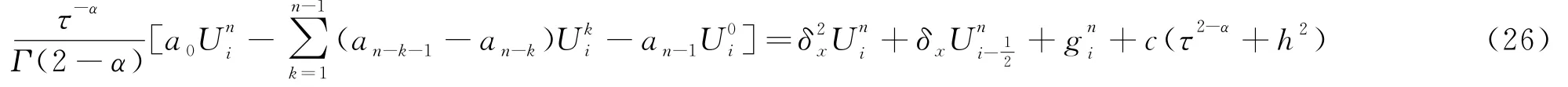
其中c是正常数,aj=(j+1)1-α-j1-α,j=0,…,n-1;1≤i≤M-1,1≤n≤N.
考虑初边值条件有
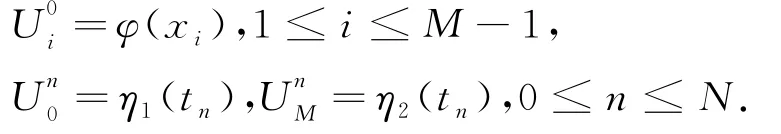
引理2[9]设α∈ (0,1),aj=(j+1)1-α-j1-α,j=0,1,2,…,则
(1-α)j-α 在(26)式中省略余项可得(7)式的差分形式 记 s=ταΓ(2-α). 定理2 差分形式(27)是唯一可解的. 证明:记 由(27)我们知道u0已知,现在设前n个值u0,u1,…,un-1已唯一确定,则由(27)可得关于un的线性方程组.要证明它的唯一可解性,只需证明对应齐次方程组 有且仅有零解. 设 ‖un‖∞=||,其中in∈ {1,2,…,M-1},将(29)改写为 上式中令i=in,并取绝对值,再利用三角不等式得 所以‖un‖∞=0,从而un=0. 由归纳法可知定理成立. 定理3 设{|0≤i≤M,0≤n≤N}为差分方程 的解,则有 其中 证明:将(30)改写为 即 设 ‖un‖∞=||,其中in∈ {1,2,…,M-1},上式中令i=in,并取绝对值,在利用三角不等式得 于是 由引理2知 从而 对不等式(31)由数学归纳法得 定理4 设|0≤i≤M,0≤n≤N}是微分方程(7)的解,{uin|0≤i≤M,0≤n≤N}是差分形式(27)的解,令 则有 ‖en‖∞≤c TαΓ(1-α)(τ2-α+h2),1≤n≤N. 证明:(26)与(27)相减得误差方程 由定理3可知
3.2 唯一可解性


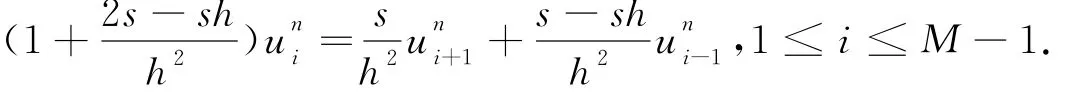
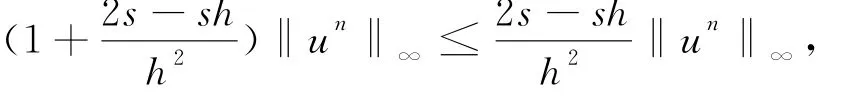
3.3 稳定性
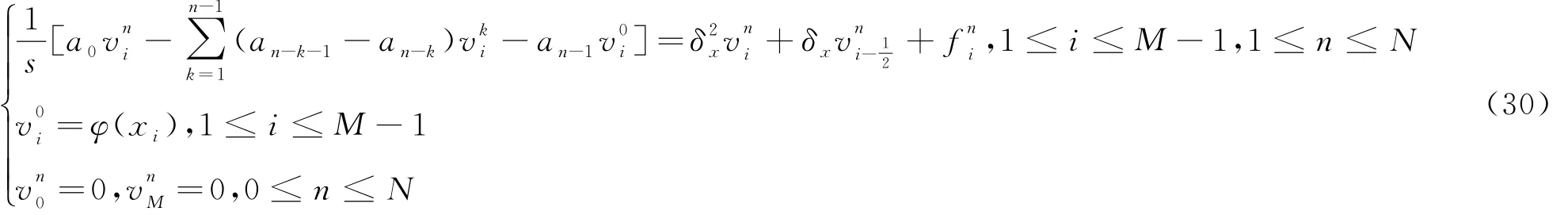
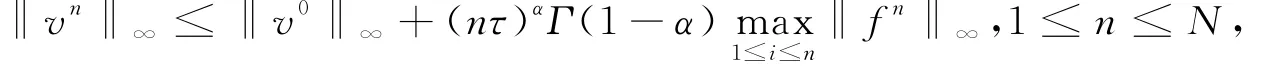
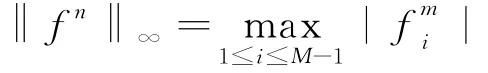
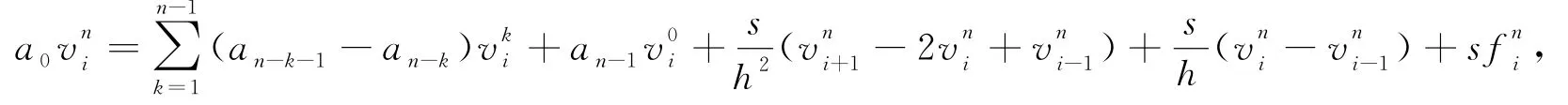
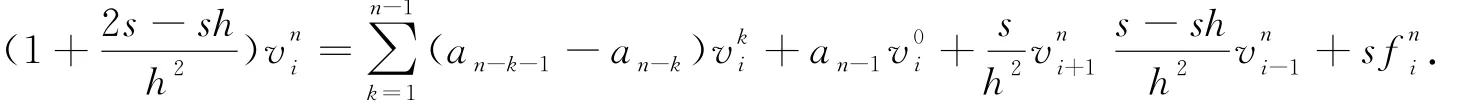
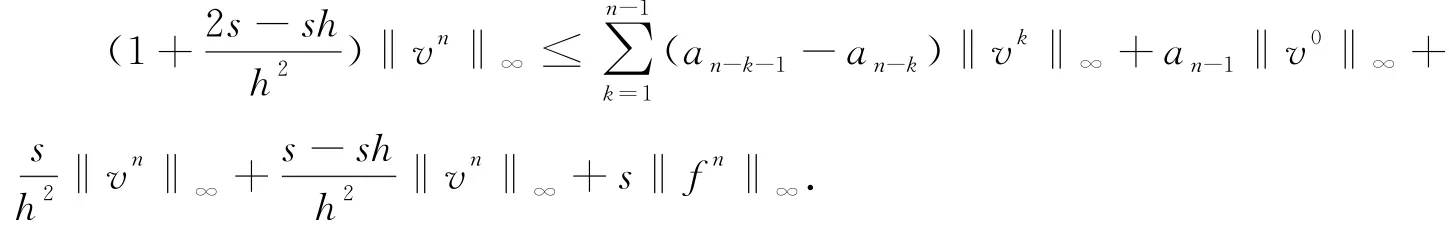
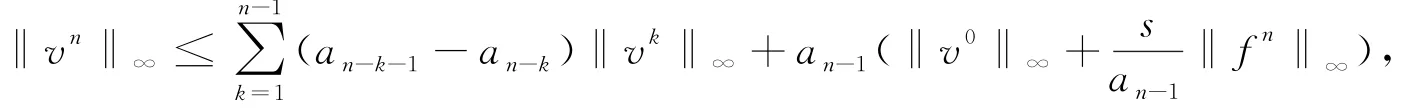
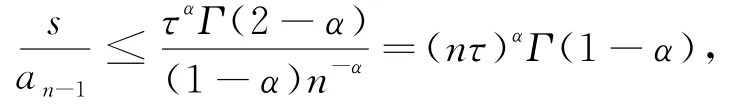
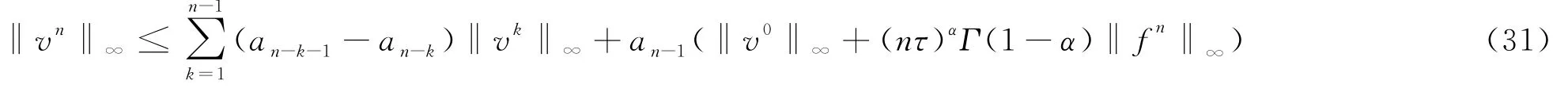

3.4 收敛性