快递包装回收中的三方演化博弈

徐 杰，胡大伟，梁一为

(长安大学 汽车学院, 西安 710064)

0 引言

快递行业的高速发展使得快递包装物的消耗量急剧攀升，这对生态环境造成了巨大的压力，政府也为此支付了相当大的治理费用[1]. 快递包装的回收利用已经成为了政府、社会和快递企业3方关注的焦点.

在快递包装回收方面，国内外的研究多集中在回收模式的选择与回收网络规划上. 李正军[2]研究了包装物的回收与循环利用问题，在对包装物回收模式分析的基础上，建立包装废弃物回收运营模型，张雯雯[3]综合分析了包装的材料、规格尺寸及回收体系等,建立低碳环保的快递包装回收体系,从而节约了成本,提高了环保效益. Shi等[4]利用集合责任分担的方法，构建出了3种逆向渠道的再制造模型，分别代表了零售商、制造商和第3方. Kim等[5]着重研究了关于废弃物回收的网络构建问题，建立了整数规划模型，并设计了多阶段的分支定界算法进行求解. 邓学平[6]以成本最小为目标函数，并引入软时间窗约束，同时还考虑了顾客的满意度. 张鹏[7]全面分析了当前快递包装废弃物循环再利用的现状，并提出提高包装废弃物利用率的举措. 李梦烨[8]研究了循环快递包装箱，并以企业的运营模式为基础，设计了逆向物流网络，构建了包装物回收物流网络优化模型，并求解了该问题.

综上所述国内外学者对快递包装回收的回收模式和回收网络设计研究较多，但很少有学者从博弈论角度出发，研究快递包装回收产业链中的相关利益方的策略选择. 本文将基于演化博弈理论，假设博弈主体均是有限理性，且信息不对称的情况下构建政府、消费者和快递公司之间的3方演化博弈模型，并运用Matlab软件进行仿真计算，从而为循环经济下的快递包装物回收产业链提供理论参考.

1 三方演化博弈模型

1.1 基本假设

假设1在本文的博弈模型中，政府、快递公司均是有限理性；

假设2政府、快递公司和消费者都是独立随机选择各自策略. 其中政府的策略集为{监管，不监管}，快递公司的策略集为{回收，不回收}，消费的策略集为{参加，不参加}；

假设3快递公司回收快递包装，包装得到循环利用，将会给政府带来社会和环境效益；

假设4消费者通过其他渠道处理快递包装会对环境带来破坏，政府因为治理环境而要支出相应的费用.

1.2 参数设置与说明

1.3 政府、快递公司、消费者的收益矩阵

1.4 模型构建

构建模型涉及的参数如表3所示.

具体表示如式(1)～(12)

U1=y[z(-C0-E0+F0)+(1-z)(-C0-
E0-D0)]+(1-y)[z(-C0+
E1-D1)+(1-z)(-C0+E1-D0)]=
y(zF0-E0-E1+zD1)+(zD0-zD1-C0+E1-D0)

(1)

表1 参数表

U2=y[zF1+(1-z)-D0]+
(1-y)[z(-D1)+(1-z)(-D0)]=
yzF1+yzD1+zD0-zD1-D0

(2)

U政=xU1+(1-x)U2=
xy(zF0-zF1-E0-E1)+x(-C0+E1)+
yz(F1+D1)+zD0-zD1-D0

(3)

表2 政府、快递公司、消费者收益矩阵

表3 构建模型参数

U3=x[z(-C1+E0+H)+(1-z)(E0-C1)]+
(1-x)[z(-C1+H)+(1-z)(-C1)]=
xE0+zH-C1

(4)

U4=x[z(-E1)+(1-z)(-E1)]+
(1-x)[z(-C1+H)+(1-z)(-C1)]=-xE1

(5)

U快=yU3+(1-y)U4=xy(E0+E1)+yzH-
yC1-xE1

(6)

U5=x[y(M0-C2)+(1-y)(M1-C2)]+
(1-x)[y(M0+C2)+(1-y)(M1+C2)]=
yM0-yM1+M1-C2

(7)

U6=0

(8)

U消=zU5+(1-z)U6=yzM0-yzM1+zM1-zC2

(9)

根据演化博弈理论，构建出：

(10)

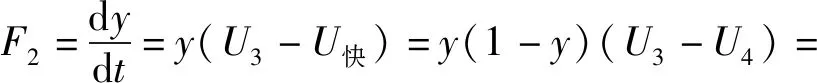
(11)

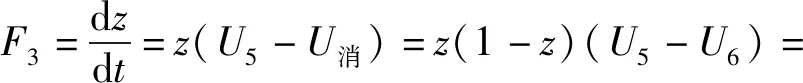
(12)

由式(10)～(12)可得在平衡状态下的均衡点有9个，分别是E1(0，0，0)，E2(0，0，1)，E3(0，1，1)，E4(0，1，0)，E5(1，0，0)，E6(1，1，0)，E7(1，0，1)，E8(1，1，1)，E9(x*，y*，z*)其中式(13)～(16)

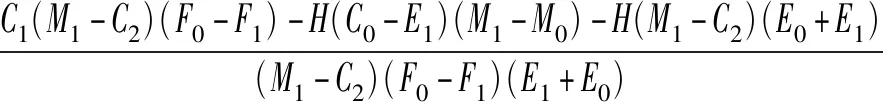
(13)

(14)

(15)

对求解出的平衡点进行雅可比矩阵分析，雅可比矩阵如式(16)：

(16)

当且仅当(1)tr(J)<0;(2)det(J)<0两个条件同时满足时，所得的均衡点才是演化稳定策略. 本文中9个均衡点中的7个点只有在满足一定条件下为系统的稳定点，如表1所示.

表4 政府、快递公司和消费者3方演化博弈稳定点

2 模型稳定性分析

1)分析点(0，0，0)稳定性

根据政府、快递公司与消费者的3方演化博弈点(0，0，0)的参数取值条件，取E1=0.5，C0=3，M1=0.5，C2=1.5，并取C1=2，F0=1，F1=0.5，H=1，M0=2，E0=0.5并且依据参数条件分别倾向于不监管、不回收、不参与的x，y，z的初值取(0.2，0.2，0.2)和倾向于监管、回收、参与的x，y，z的初值取(0.8，0.8，0.8)两组具有显著对比的初始值，得到稳定点的数值方正结果如图1所示.

此时政府监管时的收益小于政府监管所付出的成本时，政府为了减少管理费用的支出，会选择不监管；快递公司由于构建逆向物流而不能获得收益，从而选择不回收；由于消费者参与回收的收益小于其支出的成本，其往往会选择参与的策略. 此时，3方都未参与到快递包装的回收过程中，包装的循环使用面临巨大的困难.

2)分析点(0，0，1)稳定性

根据政府、快递公司与消费者的3方演化博弈点(0，0，1)的参数取值条件，取E1=0.5，C0=3，M1=1.5，C2=0.5，并取C1=1.5，F0=1，F1=0.5，H=1，M0=2，E0=0.5并且依据参数条件分别取倾向于不监管、不回收、参与的x，y，z的初值取(0.2，0.2，0.7) 和倾向于监管、回收、不参与的x，y，z的初值取(0.8，0.8，0.3)两组具有显著对比的初始值，得到稳定点的演化过程如图2所示.

图1 不同初值下稳定点(0，0，0)演化过程

图2 不同初值下稳定点(0，0，1)演化过程

图3 不同初值下稳定点(0，1，1)演化过程

此时政府监管时所支付的管理费用会大于其因公信力提升带来的收益，政府为了减少财政支出，选择不监管；快递公司参与回收所获得的收益小于其构建逆向物流所支付的费用，快递公司会选择不回收；消费者在环保意识的作用下会选择参与回收，且获取的经济利益大于其支出的成本，最终消费者选择参与的策略.

3)分析点(0，1，1)稳定性

根据政府、快递公司与消费者的三方演化博弈点(0，1，1)的参数取值条件，取E1=1，C0=2，M1=1.5，C2=0.5，C1=0.5，F0=1.5，F1=1，H=1，M0=1，E0=1并且依据参数条件分别取倾向于不监管、回收、参与的x，y，z的初值取(0.2，0.7，0.7)和倾向于监管、不回收、不参与的x，y，z的初值取(0.8，0.3，0.3)两组具有显著对比的初始值，得到稳定点的演化过程如图3所示.

此时政府选择监管时的支付的费用大于不监管的损失，所以政府会选择不监管，以避免管理费用的支出. 快递公司由于收益大于其构建逆向物流的成本，从而选择回收. 消费者由于环保意识会选择积极参与回收，且能获得净收益，因此消费者选择参与的策略.

4)分析点(1，0，0)稳定性

根据政府、快递公司与消费者的三方演化博弈点(1，0，0)的参数取值条件，取E1=1，C0=2，M1=1.5，C2=3，C1=2.5，F0=1.5，F1=1，H=1，M0=1，E0=1并且依据参数条件分别取倾向于监管、不回收、不参与的x，y，z的初值取(0.7，0.2，0.2)和倾向于不监管、回收、参与的x，y，z的初值取(0.3，0.8，0.8)两组具有显著对比的初始值，得到稳定点的演化过程如图4所示.

图4 不同初值下稳定点(1，0，0)演化过程

此时政府不监管的损失小于监管的收益，政府会选择监管；快递公司的收益小于其构建逆向物流的成本，快递公司会选择不回收；消费者由于环保意识一开始选择参与回收，但是由于无法获得净收益，消费者最终会选择不参与的策略.

5)分析点(1，1，0)稳定性

根据政府、快递公司与消费者的3方演化博弈点(1，1，0)的参数取值条件，取E1=1，C0=2，M1=1.5，C2=3，C1=1.5，F0=1.5，F1=1，H=1，M0=1，E0=1并且依据参数条件分别取倾向于监管、回收、不参与的x、y、z的初值取(0.7，0.7，0.2)和倾向于不监管、不回收、参与的x、y、z的初值取(0.3，0.3，0.8)两组具有显著对比的初始值，得到稳定点的演化过程如图5所示.

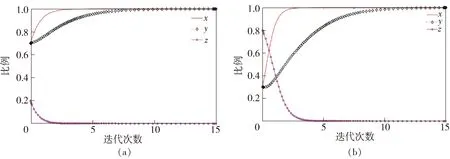
图5 不同初值下稳定点(1，1，0)演化过程

此时政府监管时的收益大于政府监管所付出的成本时，政府选择监管. 快递公司由于收益大于其构建逆向物流的成本，会选择回收. 此时由于消费者参与回收的收益小于其支出的成本，其选择不参与的策略.

6)分析点(1，0，1)稳定性

根据政府、快递公司与消费者的3方演化博弈点(1，0，1)的参数取值条件，取E1=1，C0=2，M1=1.5，C2=0.5，C1=3.5，F0=1.5，F1=1，H=1，M0=1，E0=1并且依据参数条件分别取倾向于监管、不回收、参与的x，y，z的初值取(0.7，0.3，0.7)和倾向于不监管、回收、不参与的x，y，z的初值取(0.3，0.7，0.3)两组具有显著对比的初始值，得到稳定点的演化过程如图6所示.

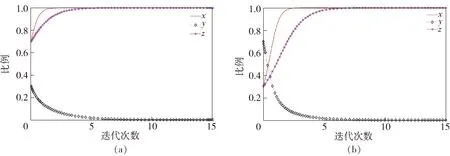
图6 不同初值下稳定点(1，0，1)演化过程

此时政府监管时的收益大于政府监管所付出的成本，政府会选择监管；快递公司由于收益小于其构建逆向物流的成本，其会选择不回收；此时由于消费者参与回收的收益大于其支出的成本，消费者会选择参与的策略.

7)分析点(1，1，1)稳定性

根据政府、快递公司与消费者的3方演化博弈点(1，1，1)的参数取值条件，取E1=1，C0=2，M1=1.5，C2=0.5，C1=2.5，F0=1.5，F1=1，H=1，M0=1，E0=1并且依据参数条件分别倾向于监管、回收、参与的x、y、z的初值取(0.6，0.6，0.6)和倾向于不监管、不回收、不参与的x、y、z的初值取(0.4，0.4，0.4)两组具有显著对比的初始值，得到稳定点的数值方正结果如图7所示.

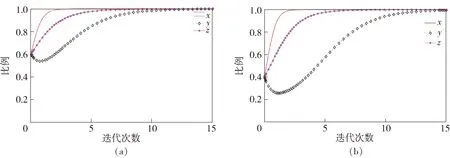
图7 不同初值下稳定点(1，1，1)演化过程

此时政府监管时的收益大于政府监管所付出的成本，政府会选择监管；快递公司一开始获得的收益无法弥补其支出的成本，但是随着政府宣传力度的加强，消费者参与人数的增多，快递公司将会获得净收益，其最终会选择回收；此时消费者在环保意识和经济利益的双重驱动下会选择参与的策略.

3 总结

本文是构建了政府、快递公司和消费者对于快递包装回收的3方演化博弈模型. 基于对各个稳定点的分析的基础上可得：

1)研究揭示了政府监管时带来环境效益等收益和管理费用等支出对政府策略选择的影响. 当政府因为监管，社会环境效益较高，且所支付的管理费用较低，政府会选择监管. 因此，政府应该积极监管快递包装物回收产业链，出台相关优惠政策，这有利于提升政府在群众中的公信力，减轻快递包装无序处理对于环境的压力. 同时，政府需要提高宣传强度，号召更多的消费者参与到快递包装的回收.

2)研究揭示了快递企业构建逆向物流的成本和收益对于快递公司策略选择的影响. 当快递公司参与快递包装物回收时获得的收益大于其参与回收所支付的成本时，快递公司会选择构建逆向物流，积极回收快递包装物. 因此，政府应该加大对实施快递包装回收的快递公司的补贴力度，以帮助企业缓解其在构建逆向物流初期所支付的高昂成本，同时还应对未实施快递包装回收的快递公司进行惩罚，以促使企业积极参与快递包装回收.

3)研究揭示了成本对于消费者策略选择的影响. 当消费者参与快递包装回收的时间成本和距离成本超过其所获得的收益时，消费者基于经济利益的考虑，会选择不参与的策略. 因此，政府应该做好快递包装物回收基础设施的建设，以减少消费者的时间成本和距离成本. 快递公司也可在送快递的时候，同时提供快递包装物回收的服务，以此来增加消费的经济利益和便利性.

本文建立的政府、快递公司和消费者的3方演化博弈模型仅对政府、快递公司和消费者之间的博弈行为进行了讨论，但是快递包装回收是一个复杂系统，其牵涉的利益相关方还有很多：如快递包装生产商、梯级利用企业等. 博弈方越多，其系统就越复杂，这也是将来进一步的研究方向.