土地利用与交通交互下的可持续道路网络设计
吴珂琪
(北京市交通委员会行政审批服务中心, 北京 100161)
0 引言
交通网络设计问题(Network Design Problem)是交通规划研究领域一个重要的研究内容. 按照决策变量的不同,网络设计问题可以分为离散网络设计问题、连续网络设计问题和混合形式的网络设计问题三大类. 其中离散决策变量对应的网络设计问题主要解决的是如何在现有网络中增加新的路段以使交通网络状况达到最优;连续决策变量对应的网络设计问题主要研究如何改善现有网络中的路段使得整个网络达到最优[1-2]. 目前,已有大量学者对相应的网络设计问题进行了研究,如Long et al等[3-5]研究了基于静态方法的路网设计问题,模型基于Wardrop原理或其随机扩展,用于描述旅行者的路径选择行为. 另一些研究进一步考虑了出发时间选择如Lin等[6]. 上述方法易于理解,但无法描述长期出行需求变化、交通网络、土地使用情况以及土地与交通之间的交互关系. 但现实中,土地利用与交通是交互影响的,当道路新建或拓宽时,区域之间出行成本的降低将直接造成区域之间的可达性增加,可达性同时将会引起人口及就业分布的变化,从而造成新的交通需求的产生,新的交通需求又会直接造成新的交通瓶颈. 李同飞等[7-8]考虑了土地利用及交通之间的交互关系,在现有交通网络的基础上,考虑就业和居住人口的空间分布和水平,以及他们之间的相互作用关系. 虽然上述研究均考虑了土地利用与交通之间的交互关系,但无法观测时间演化下的需求变化. 同时,目前对于可持续的道路网络设计问题,大部分研究仅关注社会、经济、环境的1个部分或2个部分. 本研究将考虑总车辆排放、消费者剩余变化、总用户成本贴现方差作为可持续性指标,对道路网络设计进行了研究.
1 双层规划模型
本文考虑了在规划时间[0,T]多个OD的多式交通网络构建了一个多目标双层规划模型. 规划时间定义为10~50 a不等,同时划分为N个设计周期,而设计周期定义为1~10 a不等. 将网络进一步划分为M个子网络,每个子网络对应1个交通方式,便于考虑每种交通方式的特性. 这里的交通方式可以是单种交通方式,也可以是多种交通方式. 为更清晰的阐述模型,将模型中涉及的相关符号归纳在表1中.

表1 模型符号及参数

续表1
1.1 上层模型
上层问题主要考虑了可持续指标,并将设计及财政等作为约束条件,具体为通行能力约束、道路收费约束及成本回收约束.
1.1.1 可持续性指标
本文主要考虑4个可持续指标,即车辆总排放量、消费者剩余的变化、土地所有者贴现利润的方差和广义用户成本的方差.
1)总车辆排放
车辆排放可以分为路段车辆排放及整体车辆排放,路段车辆排放考虑的是单一路段车辆的排放量,而整体车辆排放则考虑了整个路网的车辆排放. 根据在Yin、Lawphongpanich (2006) 和Ng and Lo (2013)的研究,如式(1):
(1)
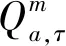
(2)
(3)
由式(2)可知,该路段上的车辆总排放量为该路段上所有交通方式的车辆总排放量之和,对于每种交通方式,该路段车辆总排放量为排放因子与交通流量的乘积. 式(3)表示车辆总排放量Q为各时期车辆总排放量的总和.
2)消费者剩余变化
消费者剩余(CS)衡量的是消费者愿意为旅行支付的费用和他们实际支付的费用之差. 它将网络拥堵和公众出行倾向的影响内在化. 对于相同的网络和需求特性,更高的CS意味着更好的系统性能. 因此,在制定网络改进计划时,实施的网络改进应增加CS. 假设网络改善前,CS为定值,则在本文中,将CS的变化值作为可持续化发展目标.
(4)
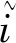
3)总用户成本贴现方差
采用广义用户成本方差之和来表征总用户成本代际公平程度,同时,总用户成本转换为现值,表示见式(5):
(5)
式中τ时段OD对ij间的综合出行成本cij,τ可采用式(6)表示:
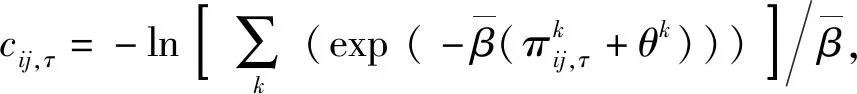
(6)
1.1.2 上层约束条件
1)通行能力约束
该约束是为了解决由于空间限制问题,路网内的路段不能建造或拓宽超过通行能力上限:
(7)
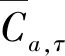
2)道路收费约束
由于政治因素等,有些特定路段不得收费,或收费不能设置过高,于是约束可表示为式(8)、(9):
(8)
(9)
3)成本回收约束
成本回收可分为3种类型:部分回收、全部回收和盈利回收(Lo and Szeto,2009). 部分(全部)成本回收发生在设计阶段的成本由收入部分(全部)回收,调整为现值. 当以现值计算,收益大于成本,且在计划周期结束时出现盈余或利润时,就会发生可盈利的成本回收. 这3种成本回收机制能采用式(10)来描述:
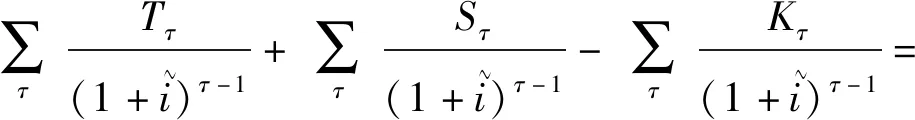
(10)
τ时期道路收费收入Tτ及改善维修成本Kτ能采用式(11)、(12)表示:
(11)
(12)
式中,
(13)
(14)
本研究中考虑盈利回收,即:
TOP≥0,Sτ=0
(15)
1.2 下层模型
下层模型为基于时间的土地利用交通问题,类似于Szeto et al. (2010)研究中描述的下层模型. 下层模型可表示为基于时间的劳拉(Lowry)模型及基于时间的方式划分及流量分配模型.
1.2.1 基于时间的劳拉模型
劳拉模型是用来预测人口和就业分布的(Lowry,1964). 劳拉模型将区域人口划分为基本部类、非基本部类及家庭3种部类. 基本部类代表生产业,基本部类的就业员工可称为基本就业,基本部类一般位于研究范围周边. 非基本部类是为居民或群体提供服务的部类,选址一般是基于人口数量的. 家庭部类由居住人口组成,这一部类数量通常与基本部类及非基本部类提供的工作岗位数有关.
基于时间的劳拉模型将劳拉模型扩展到一个动态框架体系下,每个设计阶段均需要保持劳拉模型均衡. 采用重力类模型描述通勤出行量:
(16)
高的βr意味着居民愿意选择距离工作岗位较近的地方居住,为更清楚描述βr对出行成本的影响,可将式(16)改写为式(17):
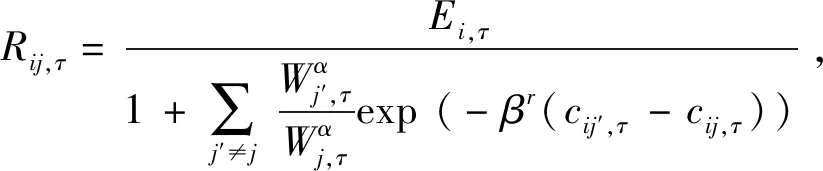
(17)
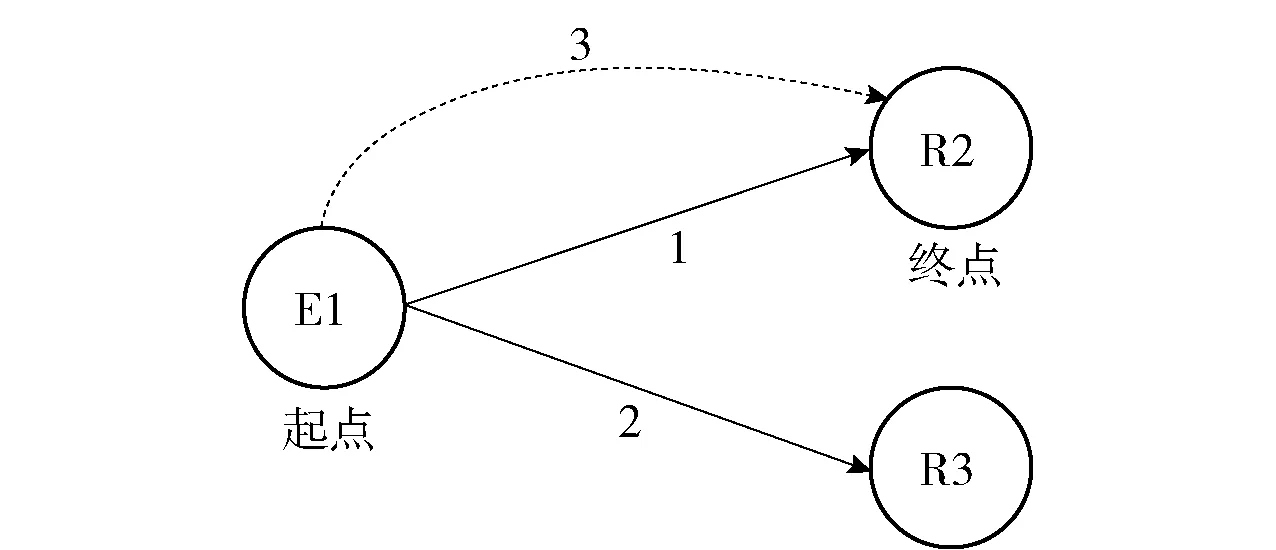
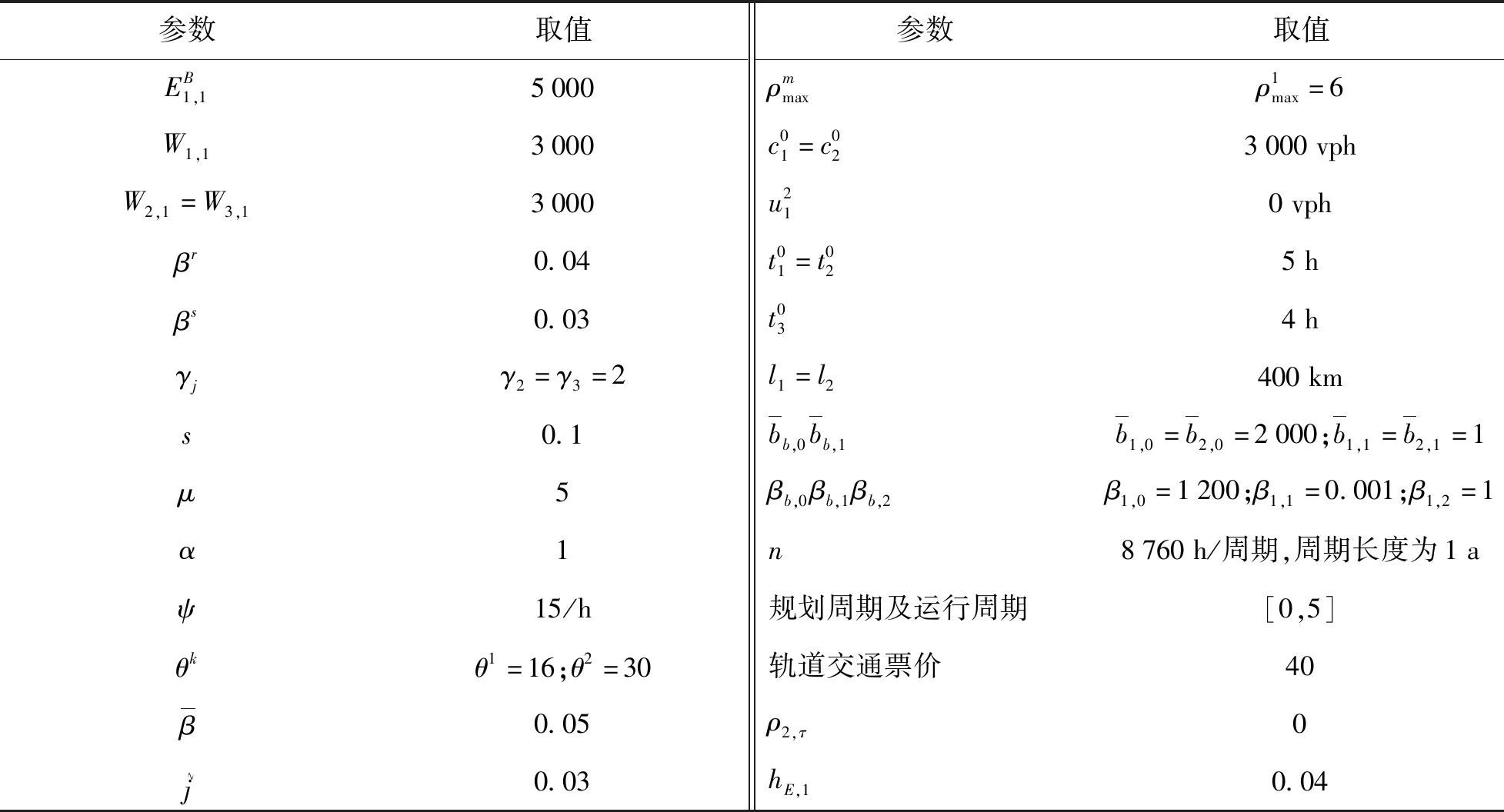
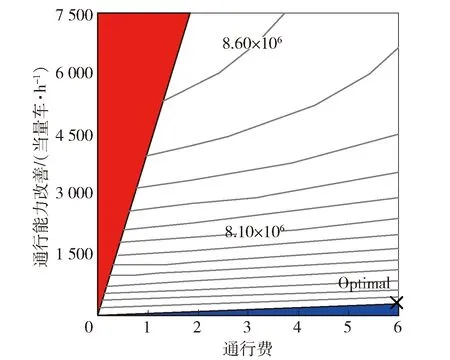
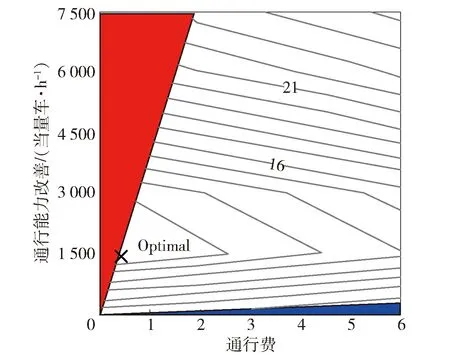
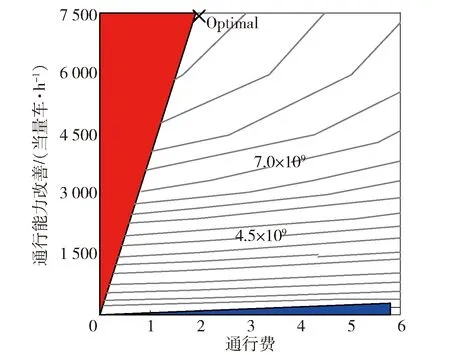
根据实际情况,一般区域内出行阻抗将低于跨区域出行阻抗,因此,cii,τ 同样,采取重力类模型描述服务就业与居民人数之间的关系: (18) 模型还需要考虑总就业人口的守恒,即: (19) (20) (21) 时期τ区域j的总居民数量,Rj,τ,可采取式(22)表示: (22) 1.2.2 基于时间的方式划分及流量分配模型 1)wardorp第一原理 依赖于时间的交通方式划分/分配约束在这个交通模型框架下描述路径及方式划分. 下层采取用户均衡原理. 首先,对于各时期τ每种交通方式k,同一OD对之间每条线路的旅行成本必须相等且最小. 可采用式(23)表达: (23) (24) 出行成本取决于流量、网络特性(如自由流量的旅行时间和道路容量)以及出行费用(如道路收费和票价). 路径成本取决于路径流量,其中路径流量取决于路段流量,其中路段流量可用式(25)表示 (25) (26) 路段阻抗函数与路段a出行时间是密不可分的,且与其他路段上的流量有关. 由于本文的聚焦于道路网络设计,于是,采用了一般的阻抗函数: (27) (28) (29) 于是,τ时段OD对ij间的综合出行成本cij,τ可表示为式(30): (30) 综合出行成本将在Lowry模型(16)和(18)中使用,并且依赖于每种交通方式的最小旅行成本. 2)方式划分模型 采用logit模型描述,如式(31)~(33)所示: (31) (32) (33) 双层规划模型可以采取如下形式表示: Uminyi(x) s.t.yi(x)≤εj,∀j≠i 式(7)~(15) Lminf=g{h(R,c(f),c(f)} s.t. 式(23)(24),式(33) 式中,x为决策变量向量,包括通行费和通行能力提高;εj为期望水平或第j项可持续指标的最大可接受值;yi(x)为第i项可持续指标,同时将目标设置为最小化. 例如,我们考虑经济可持续性,当我们期望ΔCS越大越好时,我们可以设置yi(x)=-ΔCS;当我们期望环境可持续性时,我们可以简单设yi(x)=Q. 众所周知,一般的网络设计问题都是NP-hard,难以求解. 因此,文献中提出了各种元启发式方法. 人工蜂群算法(ABC)被用于解决公交网络设计问题,且性能优于GA (Szeto和Jiang 2012). 本文将采用混合人工蜂群算法(ABC)来求解双层问题,其中上层问题采用ABC算法,下层定点问题采用MSA算法和Frank-Wolfe算法. 图1 求解方案图示 为了在ABC中生成初始解,提出了一种基于路段的生成过程. 对于每个候选路段,生成一个介于1和N+1之间的随机数,用以确定通行能力改善的时间和大小,其中N+1表示没有改善. 剩余允许改善能力定义为总允许改善能力与累计改善能力之差,然后逐期得出扩建方案. 然后,我们将扩容前路段的收费水平设置为0. 扩展后第1年的收费是随机设置的,在0和最大允许收费之间随机选择一个值. 在接下来的时间里,通行费要么保持不变,要么以固定的增量增加,同时保持通行费低于最大允许值. 按照这些步骤,自动满足收费约束和通行能力约束. 其他约束通过在定义为通过适应度函数f中引入惩罚项来处理: (34) 式中,C为足够大的常数,以避免产生负适应度值;pi为可持续性约束i的惩罚值. 若第i个指标yi不符合约束条件yi(x)≤εi,于是惩罚项max ((yi-εi),0.0)为正,以降低适应度值. 由于不同指标值的大小差异较大,不符合约束条件时均由i进行归一化,使其按比例取值. 若TOP为负(如不满足成本回收约束),于是惩罚项max (-TOP,0.0)为正. 若均满足约束条件,适应度函数将不会调整. 邻域解的生成方法如下:首先,随机选择一个候选路段,然后采用与上一段所述的方案生成过程相同的方法对其收费和能力提升方案进行了重新设计. 在这种情况下,不需要特定的补救程序来确保满足收费和通行能力约束. 为了求解下层模型,每一阶段采用连续平均法(MSA) 2次. 每个周期的算法步骤如下,其中CR和Cq定义为迭代计数器,其倒数为步长. 步骤0采取ABC算法得出上层模型解; 步骤1初始化Rij,τ,∀ij等于相应的基年居民人数,同时设置CR=0; 步骤2设置CR=CR+1; 步骤3求解方式划分/分配问题; 步骤3.1设Cq=Cq+1; 步骤3.3根据式(30)计算综合成本cij,∀ij; 步骤3.4采取式(31)依据第3.3步cij计算qk′ij,τ,∀ij,k; 图2 案例网络 通过2个实例验证了模型的性质和算法的有效性,使用1个小型网络来说明不同目标之间的关系. 网络如图2所示,这个网络中有3个路段,路段1和路段2的旅行时间由BPR函数得出,路段3具有独立路权,可理解为轨道交通线路,如图2的虚线所示. 也有3个区域:E1、R2和R3,其中“E”代表就业区,而“R”代表居住区. 假设每个区域的吸引力函数如式(35): (35) (36) 这3个区域形成2个OD对:E1-R2和E1-R3. 2个OD对都由道路连接,但只有OD对E1-R2具有独立路权的公交系统. 换句话说,OD对E1-R2有2种交通方式可供选择,但OD对E1-R3只有1种交通方式. 建议拓宽1号道路,收取过路费,以收回改善及维修费用. 方式1是汽车,方式2是地铁. 数值输入参数如表2所示. 表2 算例参数取值 为了清楚地说明目标之间的关系,将规划阶段通行费设置为固定值,且在第1阶段完成了能力提升. 红色阴影三角形代表无法实现成本回收或利润小于零的不可行区域,蓝色阴影三角形区域表示的消费者剩余比实施前效果还要差的不可行区域. X表示可行域内的最优目标值. 从图3中可以看出,对于给定的通行费用的基础上,车辆总排放量随着通行能力的提高而减少. 此外,在一定的通行能力改善下,车辆总排放量随通行费的增加而减少. 在目标是最小化车辆的总排放量,那么从图中可以看出最优解点是(6,350). 这是由于较高的通行费或更小的通行能力改善将会增加线路1的出行成本,导致在该线路上的出行需求减少,在出行需求不变的条件下,将增加线路2的出行需求. 因此,在数值算例场景下,路段1的排放降低量低于路段2车辆排放的增加量,整个网络排放减少. 图4显示,降低通行费或提高通行能力总体上降低了折现广义用户成本的方差. 从图5也可以看出,少量提高通行能力对降低广义用户成本是最优的,最优值为(0.4,1 500),与总车辆排放水平目标下的(6,350)相差甚远,说明2目标下的最优解存在较大的权衡关系. 图3 总车辆排放水平 图4 广义用户成本变化 图5 消费者剩余变化 从图5中可以看出,降低运力提升或提高收费减少了消费者剩余的变化. 最优解为 (1.7,7 500),与以往的最优解不同. 这意味着消费者剩余变化最大化的目标与车辆总排放量最小化目标以及折现广义用户成本最小化目标之间存在冲突. 本文提出了一种多目标时变路网设计模型,考虑土地利用与交通的长期交互作用和3个可持续性指标. 通过数值算例研究,不同目标下,最优解将会出现较大的差异性,在通行费一定的情况下,道路通行能力改善将提高总排放量水平、增加消费者剩余,而广义用户成本呈现先增长后下降的趋势. 目标间的权衡关系也有待进一步的研究.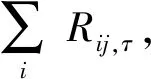

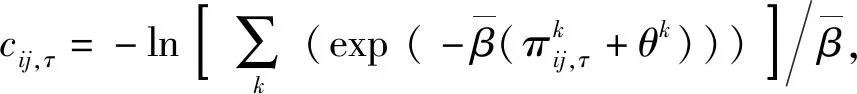
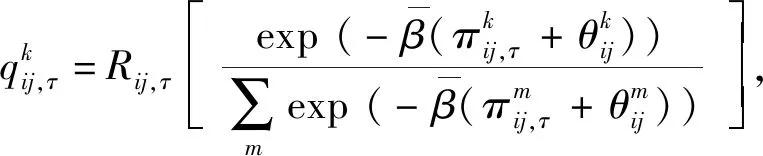
2 求解算法
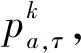


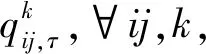
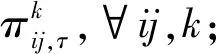
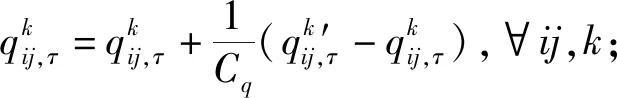
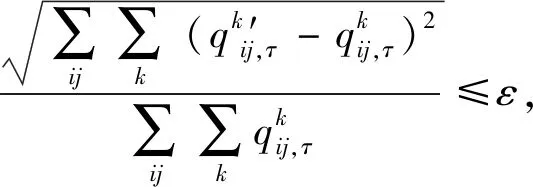
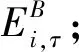
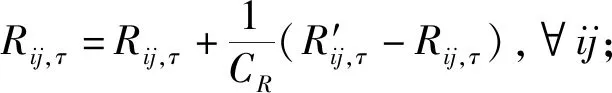
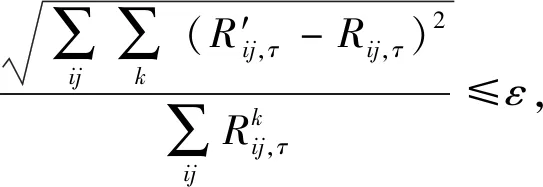
3 数值算例
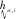
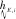
4 结束语

