工程机械齿轮箱复合故障诊断研究

孙健峰

（北京中铁天瑞机械设备有限公司，北京 100043）

［关键字］齿轮箱故障；EEMD；小波包降噪；FASTICA

在工程机械中，齿轮箱中轴承引起的故障约占20%，齿轮引起的故障约占60%［1，2］。信号分析法有短时傅里叶变换（STFT）［3］、经验模态分解（Empirical Mode Decomposition，EMD）法［4］。Jiang等将EMD和PCA结合解决信号的非线性、非稳态问题［5］，但EMD的端点效应和模态混叠现象较为严重［6，7］；针对此问题，Huang等提出集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）［8］，此算法相比于EMD来说较好地克服了模态混叠和端点效应。因此，本文选用EEMD和小波包结合，对实际工况下机械设备中齿轮箱的复合故障进行诊断。

1 集合经验模态分解

对原信号Xt局部极大、极小值采用3次样条插值，得出上包络和下包络线相应数据点m1的均值，s（t）与m的差值作为首个分量h

将h作为新的原信号s（t）继续步骤（1），直到满足下面条件为止：

（1）在运算过程中，极值点及过零点的数目相同或最多相差数目为1。

（2）在任意由局部极大值、极小值点组成的2条包络线平均值为0，可作为IMF分量使用，其中如IMF1可用c1=h来表示，则新的原信号可用r1（t）来表示

使用EEMD在加入高斯白噪声Zi（t）后，可得原信号为

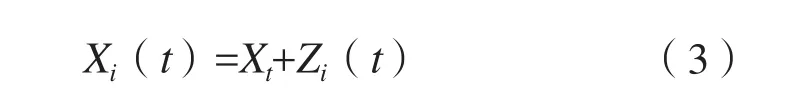
重复步骤（1）和（2），最终计算均值可得第i个IMF为

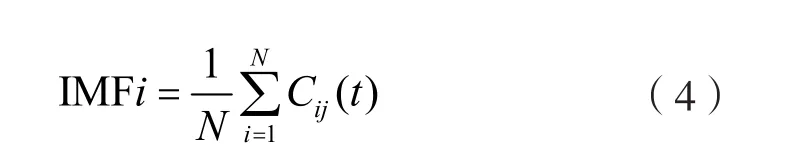
2 小波包分析

小波包分析可利用多层次进行分解，具体分解步骤为：

（1）若信号x的频率范围为［0，f］，当x的第1层被分解后可分别得到高、低频两部分D1和A1。低频信号频率为［0，f/2］，高频信号频率为［f/2，f］。

（2）在分解第2层时，分解第1层的低频信号A1得到低频AA2和高频DA2，第1层的高频信号D1被分解为低频AD2和高频DD2，相应的频率范围为［0，f/4］、［f/4，f/2］、［f/2，3f/4］、［3f/4，f］。依此类推，可将原信号层层分解，直到得到所需信号为止。

3 故障诊断流程

故障诊断流程：原信号→小波包降噪→EEMD分解→利用互相关系数筛选分量→重构信号经Fastica分离→判断故障信号。

4 实验验证

为对本文所提方法作进一步验证，采用美国DDS设备对齿轮箱进行实验验证。表1为系统相关传动频率。

表1 相关传动频率/Hz

将齿轮箱中齿轮断齿和轴承外圈点蚀共同发生故障进行试验。轴承型号Rexnord ER16K的外圈点蚀故障，点蚀直径为2mm，深0.5mm。将此故障的发生位置固定在中间轴上。电机转频采用40Hz，采样频率为10kHz，采样时间取前1s。首先利用试验设备对齿轮箱的复合故障进行采集并进行包络分析，所得结果如图1所示。

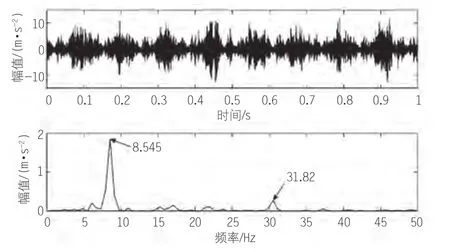
图1 复合故障信号时域图

由图1可看出，故障信号受高速轴影响较大，对其进行小波包降噪，可得降噪后信号波形如图2所示。

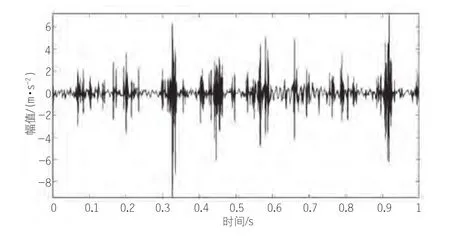
图2 降噪故障信号波形图

由图2和图1对比可知，经小波包降噪后毛刺减小，冲击成分更加突出，达到了降噪效果。对降噪后的信号再进行EEMD分解，可得其IMF分量如图3所示。

图3 IMF分量波形图

对经由EEMD分解后得到的10个IMF分量分别进行相关系数计算，结果如表2所示。

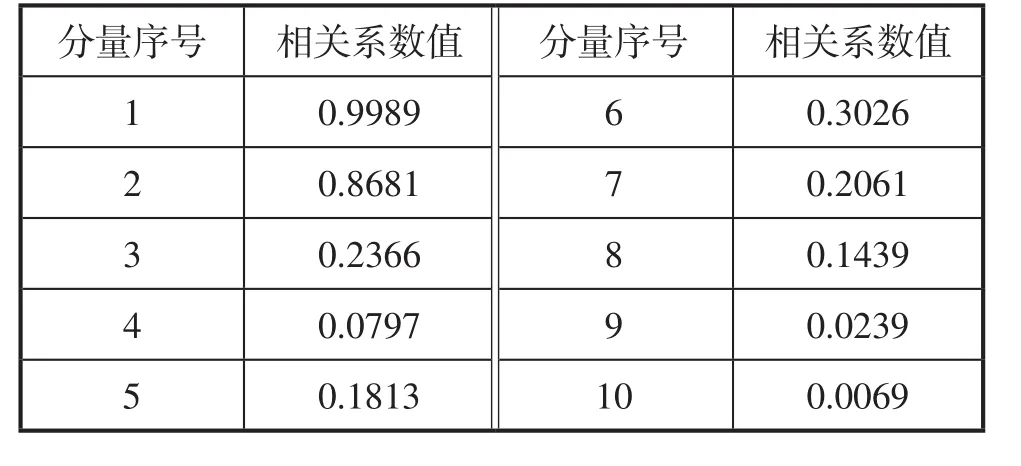
表2 10个IMF相关系数值

从表2中可知，第1、2、3、6可作为真实分量与源信号重构输入到Fastica通道中，得混合信号波形如图4所示，解混信号波形如图5所示。进一步通过希尔伯特进行包络解调提取，结果如图6和图7所示。

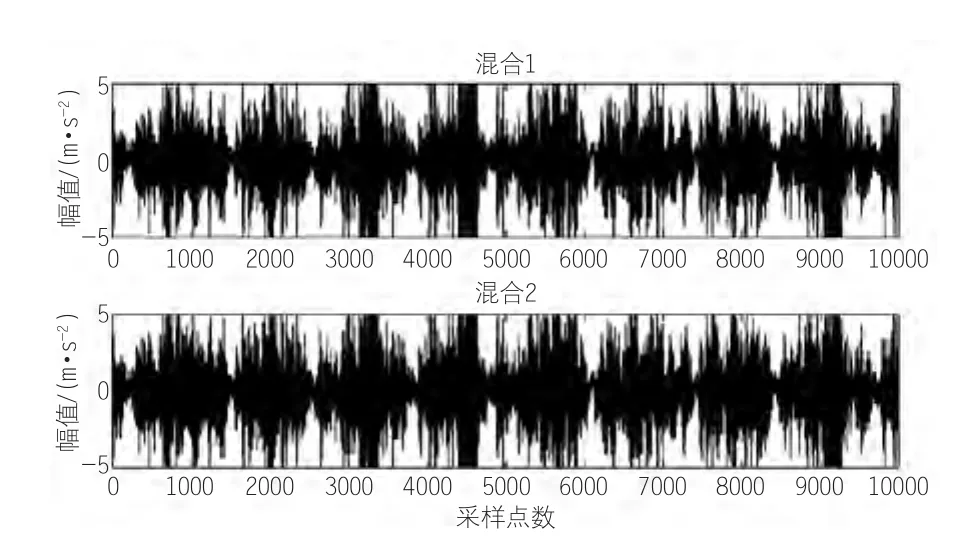
图4 混合信号波形

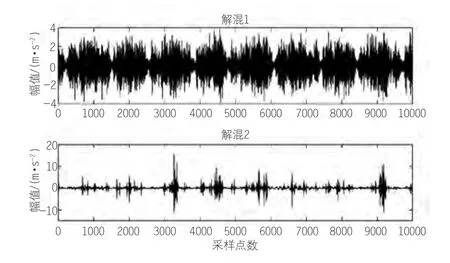
图5 解混信号波形

由图6可知，故障轴承1倍频为8.89Hz，2倍频为17.56Hz，以及由2.44Hz和中间轴转频2.5375Hz较为接近，可判断出故障发生在中间轴位置处，且高速轴对其影响被有效滤除。由图7可知，齿轮故障频率1倍频为90.99Hz，2倍频为182Hz，以及由电机转频产生的干扰信号为39Hz，故通过本文所提EEMD-小波包-Fastica方法可较好的识别判断出齿轮箱复合故障。

图6 轴承外圈故障包络谱

5 结束语

针对实际工程中齿轮箱的复合故障信号难以识别的问题，本文提出一种基于EEMD和小波包结合的方法，成功地对齿轮箱复合故障信号进行了识别判断，并通过实测有效地验证了此方法的可行性，为机械设备复合故障诊断提供了一种新思路。

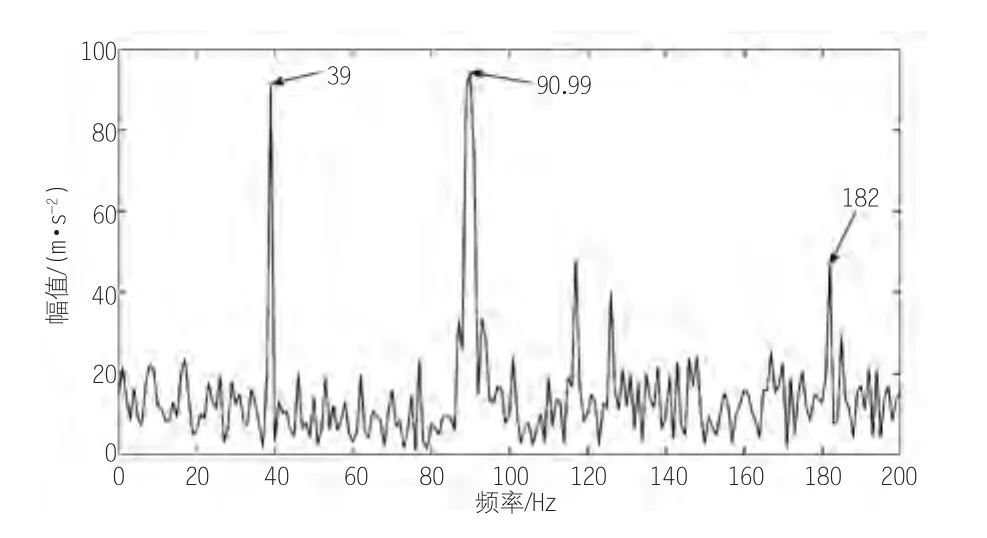
图7 齿轮断齿故障频谱