层次狄利克雷过程隐半马尔科夫模型识别飞行员脑疲劳状态

罗映雪，贾 博，裘旭益，邓平煜，吴 奇

(1.上海交通大学电子信息与电气工程学院，上海 200240;2.中国东方航空技术应用研发中心有限公司，上海 201700;3.中国航空无线电电子研究所，上海 200241)

1 引言

飞行员疲劳，也称为飞行疲劳，主要由飞行时间过长、精神状态紧张等多种不确定因素导致.飞行疲劳降低了飞行员的判断与决策能力，是飞行过程的潜在安全隐患[1-2].飞行疲劳的检测可分为主观方式与客观方式.主观方式通过飞行员填写的问卷来评估工作量负荷，进而给出对疲劳程度的判断，如美国宇航局使用任务负荷指数(task load index，TLX)作为工作量的评估指标[3];客观方式则通过记录飞行员的生理参数，如眼神追踪[4]、心率[5]等，给出疲劳状态的估计.脑电(electroencephalogram，EEG)信号作为对大脑活动的直接反映，包含了大量认知行为信息[6]，是可靠的疲劳检测指标.因此，近年来，针对脑电信号进行疲劳评估已有一定研究，如动态贝叶斯网络[7]、卷积神经网络[8]、基于模糊特征的模糊分类器[9]等方法都被应用于脑电信号的检测与分类.然而这些方法都需要人为判断并标记信号的状态，标记的正确性直接影响最终识别结果的准确度.因此，建立一个分类模型，从原始EEG信号中推理飞行员脑疲劳状态，对于确保飞行安全有重要意义.

应用脑电信号来探测脑电信号疲劳状态主要包括2个步骤:1)提取节律特征并构造疲劳指标;2)依据疲劳指标对疲劳状态进行辨识.

不同的选取方式将很大程度上影响使用EEG信号评估大脑活动状态的结果.已有研究表明，脑电波的4种节律信号:δ(0～4 Hz)，θ(4～8 Hz)，α(8～13 Hz)，β(13～20 Hz)可以反映出大脑活动的变化[10]，如在睡眠的开始阶段θ将呈上升趋势[11].目前常用的特征提取方法包括小波分析[12]、频率谱密度分析[13]、基于熵的分析[14]等.大脑活动状态评估方法包括两类:第1类是通过节律信号的变化趋势，如出现高频快波α及β时，大脑处于兴奋状态，而δ为高幅慢波时大脑活动被抑制[15];第2类是节律信号的定量指标，例如Jap等人提出了4种基于节律的功率谱比率的EEG算法[16].此外，已有研究几乎都是采用快速傅里叶变换(fast Fourier transformation，FFT)得到的频谱信息作为判断指标，然而FFT只能给出一定时间内的平均频谱信息，不能给出信号点的实时频谱信息.因此，本文建议提取节律信号的瞬时频谱信息，设计5个指标，作为评估大脑疲劳状态的特征.

第2个步骤是脑疲劳认知推理.对大脑潜状态的推理对于正确评估大脑活动及疲劳状态有重要意义.隐马尔科夫模型(hidden Markov models，HMMs)[17-18]作为隐状态学习的经典模型，已经得到了广泛应用，然而也存在一些局限，如状态持续时间分布是几何形式，可能与实际应用情况不相符，此外，还必须设置隐藏状态数量，不准确的数量将导致模型与实际数据的偏差.贝叶斯非参数方法(Bayesian non-parametric，BNP)[19]可用于解决这一问题，它可以在学习过程中推断出正确的状态数量.将BNP应用于HMM，可经由层次Dirichlet过程(hierarchical Dirichlet process，HDP)从后验分布中推断隐藏状态数量[19].HDP-HMM的一些扩展模型，如自适应HDP-HMM[20]和在线HDPHMM[21]已被应用于处理相关实际问题.此外，传统的HDP-HMM没有考虑到每个状态的持续时间，将导致状态之间的快速切换.一种可行的解决方法是使用隐半马尔科夫模型(hidden semi-Markov model，HSMM)[22]，它考虑了状态的驻留时间，进入特定状态后，驻留时间结束时，马尔科夫链将转换到下一个状态.与传统的HMM不同，HSMM的每个状态对应一段观察值.HSMM的拓展形式，如显式持续时间HSMM[23]及变量转换HSMM[24]，已被广泛应用于健康监测领域.然而在疲劳状态检测中，疲劳对脑电信号的影响非常微弱，疲劳开始的时间点很难被检测，因此本文更关注疲劳的程度，即疲劳的剩余寿命.在此基础上，本文定义基于剩余寿命的HSMM，它可以表征疲劳的程度，不关心疲劳的开始点，而关心疲劳开始以后到极度疲劳的剩余时间(寿命).因此，它能够显著地探测到疲劳状态，这正是飞行安全一直难以解决的问题，也是我们建模的出发点.关于应用该模型检测脑疲劳认知状态，目前还没有突出研究.因此，本文采用了HDP-HSMM来探测飞行员脑疲劳认知状态，它增加了疲劳状态的停留时间，使疲劳更容易被检测到.

本文结构如下:第2部分给出了EEG信号特征提取方法，即通过光滑伪仿射维格纳-维勒分布提取到更有效的大脑活动特征;第3部分在HSMM的基础上(第3.1节)介绍了HDP-HSMM 的构成(第3.2节);第4部分进一步给出了模型的学习算法，即基于剩余寿命的HSMM前向后向算法(第4.1节)、驻留时间分布的参数估计算法(第4.2节)以及HMM的Viterbi算法(第4.3节);第5部分通过实验验证，对HDP-HSMM模型的有效性进行评估;第6部分为总结.

2 特征学习

EEG信号中的4种节律δ，θ，α，β可以作为大脑活动状态评估的指标，其对应频率波段分别为0～4 Hz，4～8 Hz，8～13 Hz，13～20 Hz，主要特点及出现时期如表1所示.

将飞行员EEG信号通过db10的小波包分解，提取出节律信号.为了获取节律信号的瞬时频谱信息，本文提出了改进的基于Kaiser窗的维格纳-维勒分布(Wigner-Ville distribution，WVD).维格纳分布函数(Wigner distribution function，WDF)是分析非平稳信号的重要方法，但可能由于交叉项干扰产生负值.采用加入滑动指数窗使WV分布仿射光滑化可以有效抑制交叉项的干扰，这种改进方法称为光滑伪仿射维格纳-维勒分布(smoothed pseudo-affine Wigner-Ville distribution，SPAWVD).

表1 EEG信号节律分布频率及特点Table 1 Frequency and characteristics of EEG rhythm signals

2.1 光滑伪维格纳-维勒分布

信号的s(u)时频分布可表示为

其中:s*(u)是s(u)的共轭复数，φ(θ，τ)是核函数.根据选取核函数的不同可以产生不同的分布.当核函数φ(θ，τ)=1时，可以得到维格纳分布

能量谱密度函数p(ω)可以表示为

由此可以得到时变能量谱密度函数.对于一个连续的WDF:

其中Rt(τ)是时变自相关函数，可用对称形式表示为

另外，离散时间的WDF可表示为

当对信号s(t)进行采样时，会导致WDF中信号的混叠，避免混叠信号的有效方法是在计算WDF前利用分析信号.分析WDF也被称为维格纳-维勒分布，可表示为

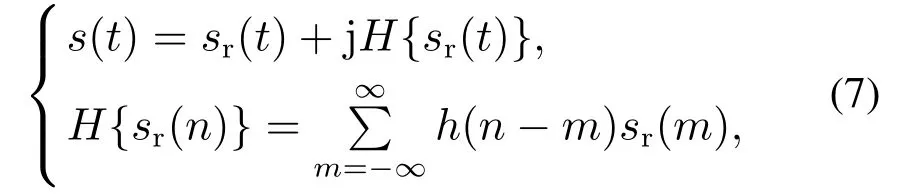
其中H{sr(n)}是Hilbert变换，由90°相移的脉冲响应h(t)的卷积生成.

为了避免干扰项影响产生的负值，在WVD中加入Kaiser窗函数G(t，w):

其中:τ是Kaiser窗的驻留时间，a是决定窗口形状的非负实数.I0是第1类的零阶修正Bessel函数.相应地，WVD可表示为

选取适当的w和t，可以得到采样的Kaiser窗函数:

其中p和q可取值于±2j和±2k之间.由采样的WDF和Kaiser窗函数的卷积，可以得到光滑伪维格纳-维勒分布(smoothed pseudo Wigner-Ville distribution，SPW VD)[25-26]:

WVD给出信号能量在时频域的直接信息，可较准确估计时域高次谐波，分辨主频率成分，但结果受交叉项干扰产生偏差.减少交叉项干扰的一种方法是引入窗函数进行滤波.SPWVD是基于此方法，在WVD的基础上加入窗函数得到的分布，即通过在时频域做平滑滤波，降低交叉项对分析结果的影响.将其应用于分析EEG信号，可减少交叉项干扰，但滤波平滑方法同时也导致时域和频域分辨率降低.

基于此，提出仿射SPWVD方法，可以表示为

其中Ψ(t，m)是光滑函数.

由于与疲劳状态相关的脑电信号集中在δ波(0～4 Hz)，θ波(4～8 Hz)，α(8～13 Hz)，β波(13～20 Hz)4个节律，提取节律信号后可构建心理认知状态的频率指标为

通常情况下，ps(ω)表示S波SPAWVD的能量谱密度大小，本文中使用SPAWVD的瞬时频谱来代替FFT的频谱.因为FFT只能在给定时间段内提供平均频谱信息，而SPAWVD能即时提供EEG信号的时频幅度信息.

3 HDP-HSMM

3.1 HSMM

假设当前时间为t，当前过程经历了n-1次状态转移，从上一次转移开始的时间为则过程{s1:T，O1:T}就是一个半隐马尔科夫过程，它的子序列(in，dn)n≥1也是一个基于马尔科夫特性的马尔科夫过程.在HSMM中，如果一个状态在时间结束，则在时间它不能转移到相同状态，因为状态的驻留时间是由几何或指数分布以外的一些分布决定的.可以定义一个一般的HSMM[22]

其中:a(i，h)(j，d)表示驻留时间为h的状态i到驻留时间为d的状态j的隐藏状态转移概率，并假定a(i，h)(j，d)对于i，j∈S，h，d∈D独立于时间t，且对于所有给定的i∈S，h∈D满足

pj(d)是状态j的驻留时间为d的概率，πj，d为状态为j，驻留时间为d的初始状态概率，即得到第1个观察值之前时间t=1的概率.bj，d(Ot+1:t+d)表示在驻留时间为d的状态j形成观察值Ot+1，…，t+d的发射概率.

对脑疲劳认知状态的监测是本文的研究重点.因此本文定义了剩余寿命的HSMM，它可以更有效地反映这种现象.定义.假设状态转移概率独立于之前的状态与驻留时间，则该模型可称为剩余寿命HSMM(remaining life HSMM)，其结构如图1所示.

1) 假定状态转移独立于前一个状态的驻留时间，从(i，h)到(j，d)的状态转移概率为α(i，h)(j，d)=αi(j，d);

2) 进一步地，假定状态驻留时间独立于前一个状态，则状态转移概率可表示为αi(j，d)=αi，jpi(d).

在剩余寿命为1时，状态i根据转移概率αi(j，τ)转移到状态j.本文关注的重点在结束时间，如在时间为1时，状态j的开始时间不是本文的主要研究对象.在脑疲劳认知状态的检测中，因为认定疲劳状态开始的行为很难检测与定义，相对于疲劳状态的开始时间，更应关注疲劳的轻重程度.对于状态j，剩余寿命τ逐渐降低到1，然后在时间t+τ结束并转换到下一个状态.处于状态j时，发射概率bj(Ot+1:t+τ)形成了τ个观察值Ot+1，…，t+τ.

图1 剩余寿命HSMMFig.1 Remaining life HSMM

HSMM的一组模型参数可以定义为

其中:αi(j，τ)为隐藏状态转移概率，bj(Ot+1:t+τ)为发射概率，pj(d)为驻留时间概率，πj，d为初始状态概率.

为了进一步简化HSMM，可以假定观察值与给定的状态相关或条件独立，即

3.2 HDP-HSMM

为解决必须设置隐藏状态数量的问题，在HSMM中加入层次狄利克雷过程(hierarchical Dirichlet process，HDP)，作为无限状态空间的先验.

狄利克雷过程可由随机概率密度分布G0与正实数α0表示

本文使用折棍(stick-breaking)过程来构造狄利克雷过程，

其中:G为随机测度，δφ为集中在φ的概率测度，πk为随机概率测度.折棍过程可记作

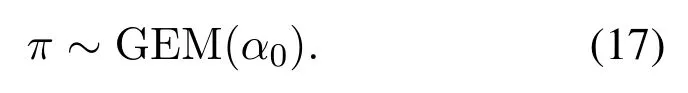
同样由折棍过程构造狄利克雷混合过程:

其中zs为xs的指示因子.

假定xij服从分布F(θij)，θji服从分布Gj，且取值为φk的概率为πjk，层次狄利克雷过程可表示为

HDP-HSMM 的生成过程与HDP-HMM 类似，可由下述表达式表示:

其中:f和g表示观察值和驻留时间分布，GEM表示折棍构造过程，γ表示Gamma函数，zs为隐藏状态序列，ds为驻留时间分布，yt为服从分布f(θ(xt))的观测序列.HDP-HSMM的基本结构如图2所示.

4 学习算法

4.1 基于剩余寿命的HSMM的前向后向算法

加入剩余寿命τ，从状态i到状态j的状态转移概率为

图2 HDP-HSMM结构示意图Fig.2 Structure of HDP-HSMM

由此，基于剩余寿命的HSMM的前向后向变量可以被定义为

再假定输出具有条件独立性，剩余寿命HSMM的后向变量可以表示为

类似地，可以得到前向变量

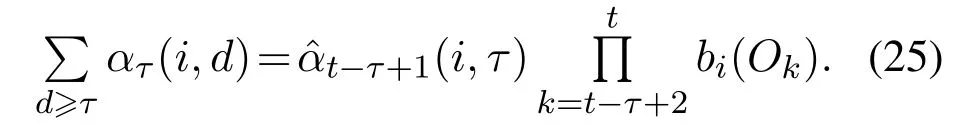
然后，剩余寿命HSMM的前向后向推导式为

假定状态驻留时间独立于先前状态，则可以通过具有明确驻留时间的HSMM的前向后向变量降低剩余寿命HSMM的计算复杂度.前向后向变量可以由下述表达式表示:

接下来可以进一步得到剩余寿命HSMM的前向后向变量

然后得到光滑概率函数

其中:ξt(i;j，d)是时间t下，驻留时间为d，状态i到状态j的光滑转换概率，ηt+d是时间t下，驻留时间为d的状态j的光滑概率.

4.2 驻留时间分布的参数估计

状态j驻留时间的概率密度函数可表示为

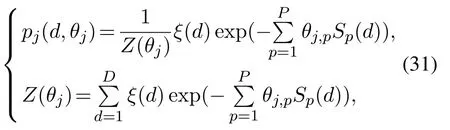
其中:P是特性参数的个数，θj，p是状态j的第p个特性参数，θj=(θj，1，…，θj，p)是状态j的一组特性参数，Sp(d)和ξ(d)是充分统计量，(θj)是归一化项.

由式(31)，

将α(i，h)(j，d)=α(i，h)jpj(d)代入式(33)，可以得出驻留时间分布的模型参数

然后，状态j的驻留时间可以估计为

状态j驻留时间分布的参数θ=(θ1，…，θM)可由下式最大化得到:

由于指数函数是对数凹函数，可以由最大似然估计求得全局最大值

是指数函数的期望值，由此，新的驻留时间参数可以被定义为

4.3 HMM的Viterbi算法

为找到一个状态实例S1:T，使P[S1:T=j|O1:T，λ]取最大值.定义Viterbi前向变量:

其中δt(j，d)表示驻留时间为d(d∈DDD)的状态j中在时间t(1≤t≤T)结束的可能性最大的部分状态序列.

为简化表示HSMM的开始时间、状态和驻留时间，本文用变量ψ(t，j，d)来表示δt(j，d).然后，对于前一个状态i*，在时间t-d结束且驻留时间为h*，可以简化表示为ψ(t，j，d)=(t-d，i*，h*).

状态序列可由先前状态的最大似然更新得到.根据HSMM的一般边界条件，前一个状态为

进一步地，简化对开始时间的假设，如令t1=T，得到

其他前向状态序列可以通过迭代得到

直到确定开始时间S1，迭代结束，其中S1=估计的状态序列为

5 实验

5.1 数据采集

1) 模拟飞行设备.

实验在6-DOF运动平台结构的飞行模拟器上进行，其外景与内景如图3所示，采用的飞行动力学模型是CRJ-200商用飞机.模拟驾驶舱具有高保真度和良好的沉浸感，机内的显示系统及仪表台提供了飞行所需的发动机转速、飞机姿态等基本参数，模拟光照条件良好.

2) 实验飞行员.

被试者为20 名男性飞行员(中国籍，飞行时长为7173.24±5270.94小时，年龄为39.06±7.75岁)，包括2名中国民航试飞员、6 名ARJ机型试飞员及2名其他航线飞行员，被试者实验前均未检测出不正常的心理及生理因素，在实验前一周的飞行时长为15至25小时，均熟悉模拟飞行器操作流程.

3) 数据采集设备.

脑电信号采集设备为穿戴可接触式的国际通用10-20系统，采样频率为160 Hz，采集的脑电信号为64通道.64个电极在设备上的空间分布如图4所示.

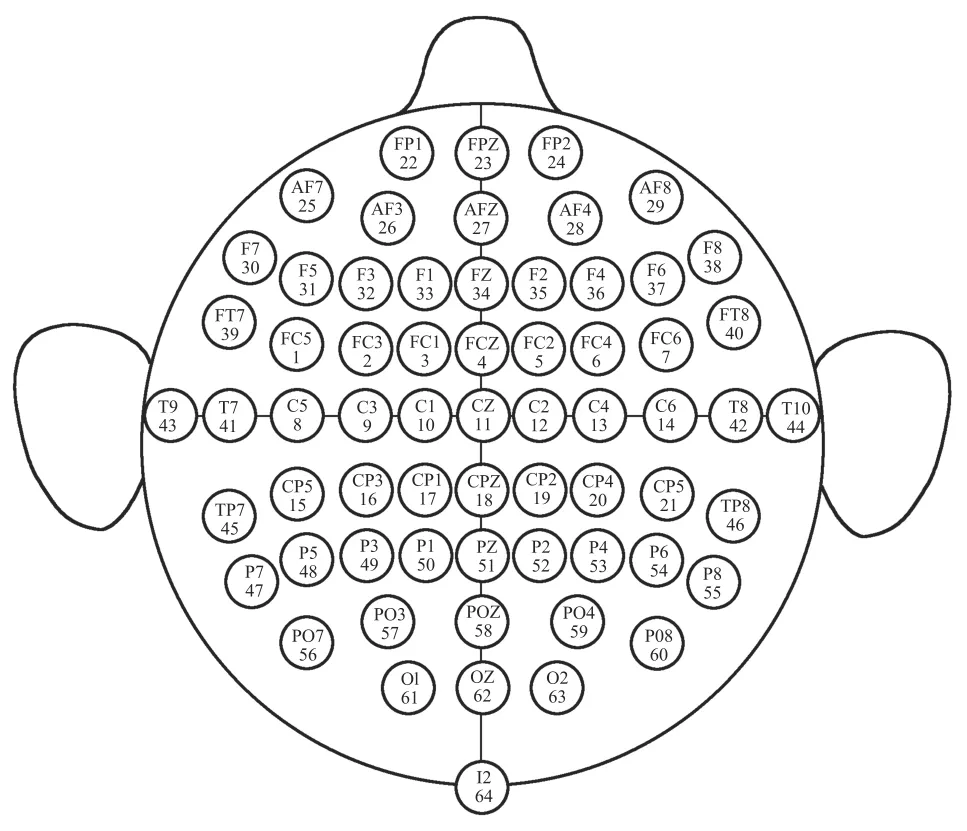
图4 国际10-20系统64电极的空间分布Fig.4 International 10-20 system 64 electrode spatial distribution

4) 实验流程.

实验当天，飞行员在进行充分休息后，于上午8点30分开始实验，在进行模拟飞行前进行第1次脑电数据采集，并且填写斯坦福困倦度量表(Stanford sleepiness scale，SSS)与卡罗林斯卡困倦度量表(Karolinska sleepiness scale，KSS)，此时采集的15 min信号为状态1，即非疲劳状态.第1次模拟飞行为1 h，在飞行后半程采集15 min的脑电信号并填写困倦度量表，此时为状态2，即轻度疲劳状态.然后进行第2次的模拟飞行并加入气流扰动，模拟复杂飞行环境，时长为45 min，同样采集后15 min的脑电信号并填写困倦度量表，此时为状态3，即中度疲劳状态.第3次的模拟飞行为起飞及降落的复杂操作模拟，时长为30 min，采集后15 min 的脑电数据并填写度量表，此时为状态4，即重度疲劳状态.数据采集实验持续2天，共采集到40份有效数据，将每段信号采集时记录的疲劳状态，即数据点标签，与困倦度量表评估的疲劳程度相比对，其中36份样本的结果一致，将其用作实验数据.

5.2 信号预处理与特征提取

由于EEG信号是弱电信号，在数据收集过程中很容易混入其他噪声，因此需先对信号进行去噪处理以减少对后续特征提取及识别过程的影响.本文选取db10的小波包对EEG信号进行分解，然后由小波系数重构去噪后的EEG信号，得到4种节律信号，如图5所示.

图5 EEG信号的节律信号Fig.5 EEG rhythm signals

为了评估SPAWVD对于分析信号频域的必要性，选择了电极位置35，42，54，62的脑电信号，基于SPWVD与SPAWVD分别对信号进行变换，得到的时频分布如图6-7所示.

图6 由SPWVD得到的时频分布Fig.6 Time-frequency distribution by SPWVD

从图6-7可以看出，SPAWVD与SPWVD均给出了脑电节律信号的瞬时三维特征(时间，频域，幅度)，但SPAWVD相比SPWVD能提取出更为丰富的瞬时局部频谱信息.

图8为疲劳状态与非疲劳状态下的复合特征，横轴为EEG样本信号段，纵轴为复合特征取值.可以看到，在疲劳状态时，各个特征取值均有上升趋势，其中的上升趋势更明显，即这3个复合特征对疲劳更为敏感，可以作为疲劳程度的判断指标.

图7 由SPAWVD得到的时频分布Fig.7 Time-frequency distribution by SPAWVD

图8 疲劳/非疲劳状态下的复合特征Fig.8 Composite features under fatigue/non-fatigue state

5.3 模型建立与识别

基于第5.2 节中构建的疲劳指标，建立HDPHSMM对EEG信号进行聚类.其中发射概率分布函数为Gaussian混合分布，参数采样为Dirichlet先验，状态驻留概率服从Possion分布.

基于HDP-HSMM对EEG信号的疲劳状态进行识别，具体实现流程如图9所示.

图9 EEG信号分类识别疲劳状态流程Fig.9 Flow chart of inferring fatigue status

将实验采集到的36份样本分为4个数据集，每个数据集包含9份样本，每份样本为1个飞行员单次实验的EEG数据，且各数据集中4种疲劳状态:状态1(非疲劳)、状态2(轻度疲劳)、状态3(中度疲劳)、状态4(重度疲劳)占比相同.对每个数据集，分别进行提取预处理并提取节律信号，由SPAWVD得到瞬时频率信息，组合成为复合特征，最后由HDP-HSMM进行聚类，得到识别结果如表2中所示.

表2 不同模型下的识别准确率Table 2 Accuracy of classification using different models

由表2中结果可以看到，K-Means作为简单易用的聚类算法，在本次实验中识别度较其他算法有明显的下降，且波动受数据集影响较为明显.HMM由于没有考虑到状态的驻留时间，导致状态间的快速切换，识别度低于HSMM.而HSMM的识别度一定程度上受到隐藏状态数量设置的影响，在数据集2中识别准确度略高于HDP-HSMM，但在其他数据集下准确度下降，验证了HDP-HSMM自动推断隐状态数量的优势.在4个数据集下，本文提出的基于SPAWVD的特征提取与HDP-HSMM状态识别方法均有较高的分类精确度.

6 结论

本文为飞行员脑疲劳认知推理提供了解决方案，总共分为两个步骤:第1步为节律与有效特征的提取，第2步为飞行员脑疲劳状态标签与推理.

特征提取部分，本文提出了采用基于Kaiser窗函数的SPAWVD的算法，计算节律信号及其组合信号的瞬时频谱特征，并将其时频分布与SPWVD的时频分布相对比，验证了SPAWVD提取的瞬时频谱特征更显著.

疲劳状态标签与推理部分，为了避免传统HMM潜状态之间的快速切换，本文提出了基于剩余寿命的HSMM对脑认知持续时间进行建模.此外，基于飞行员脑认知行为是由多通道的脑节律行为合成的整体表现行为，需要建立一个共享多通道脑电节律特性的飞行员脑疲劳认知模型.而层次Dirchlet过程(hierarchical Dirichlet process，HDP)的模型可以提供共享主题的子任务学习机制.因此，本文建立了一种基于HDP-HSMM的多通道共享DP先验参数的层次学习网络，避免了HSMM隐藏状态数量的参数先验设置问题.

评估实验是基于CRJ-200模拟器采集的飞行员EEG数据而进行的.用SPAWVD提取飞行员EEG节律特征，建立基于HDP-HSMM的飞行员的脑疲劳认知模型，对疲劳状态进行推理.在4个实验数据集下，本文提出的基于SPAWVD的特征提取与HDPHSMM状态推理方法均有较高的识别精确度.

未来的工作:本文的工作是基于中国商飞下一代飞机适航认证需求而进展的.项目组的成员有美国千人专家参与.未来的研究将扩展到恶劣环境条件下的飞行员疲劳认知潜状态具有大量离群点特征的状态转换概率建模中，使HDP-HSMM模型具有更强的飞行员脑疲劳退化性能探测能力.另外对观测脑节律进行了增强现实(augmented reality，AR)建模，研究基于HDP-AR-HSMM的飞行员疲劳脑动力交替机制也是我们未来的方向.