温室微喷空气湿度场重建的传感器优化部署研究

付 聪，郑世健，刘知贵

(1.西南科技大学信息工程学院，四川 绵阳 621000；2.中国工程物理研究院电子工程研究所，四川 绵阳 621000)

0 引 言

随着设施化温室规模的不断增大以及技术要求的提高，设施化温室的环境监测工作变得日益重要。为了应用有限的传感器资源获取温室有效的测量信息，温室传感器空间优化部署研究成为一个重要的课题。目前，土壤墒情传感器节点部署[1, 2]和WSN传感器节点部署[3]是主要关注的方向，对空气湿度传感器优化部署问题研究尚少见。

国内外进行了大量的空间传感器优化部署研究。从大量文献阅读中表明传感器部署主要可以从两方面进行优化，其一是选择适当的优化算法，目前，传感器优化部署大致分为传统和非传统算法两类。传统算法主要包括模态置信准则[4]、常规规划[5]等。以遗传算法为代表的非传统优化算法，具有较强的搜索优化能力，但大部分适用于解决连续问题，针对离散问题需要根据情况设计具体的算法。Charles等人[6]利用最小化方差和蒙特卡罗法分析了环境监测最优传感器配置方案。王邦等人[7]针对精准农业应用，提出了一种用于现场重建的新自信息覆盖模型。田桂林等人[8]利用烟花算法优化多传感器网络中总区域覆盖率和传感器利用率目标。李德春等人[9]将克隆选择和粒子群算法结合，优化了结构健康传感器优化部署方法。许可等人[10]设计了神经网络、分批估计和自适应加权平均融合算法优化温室传感器布设方案，表明该方法能够确定最优传感器布设区域；其二是选择适当的优化目标，Mohammed等人[11]以研究区域的覆盖范围和连通性为优化指标，综述了近几年无线传感节点的部署优化研究，但需要知道每个节点影响范围。东桥等人[12]以重建精度为目标，研究了声学测温传感器在粮仓中部署问题。Monireh等人[13]针对传感器部署成本最优问题，利用流体力学与遗传算法实现了停车场内传感器最优部署。

通过上述对空间传感器部署研究的分析，本文针对温室空气湿度传感器部署问题，利用连续粒子群算法框架，重新设计了问题的表示方法和速度-位置规则；目标函数使用时空协同克里金插值法构建新的优化函数，较完整的解决了温室湿度传感器优化部署问题。将该方案应用到温室环境中，结果表明该方案能够较好的反应温室环境整体湿度变化。

1 问题分析

目前温室监测主要采用中心和边缘部署少量单点传感器的方案，但空间环境因子是变化不均匀的(与具体设施有关)，若以单点传感器监测数据来控制整体的环境变化，会导致灾难性的误差。若部署大量传感器，又会影响环境作物生长和产生较高成本代价。如何选取合理的传感器数目和位置是温室精确控制研究的前提。

针对温室中空气湿度监测点部署的问题，具体部署方案接近无穷组，若将每种方案列举，其工作量大。实际情况下，监测数据总会存在一些不可避免的误差，本文将空气湿度监测点按照理想情况处理(即假设真实温度与采集温度相同)。在具体研究区域(土壤上方1 m3空间)规则部署15个传感器，并记录微喷前后空气湿度变化值。纵坐标表示节点间的相关系数之和的归一化值，横坐标表示传感器序列号，结果如图1所示。

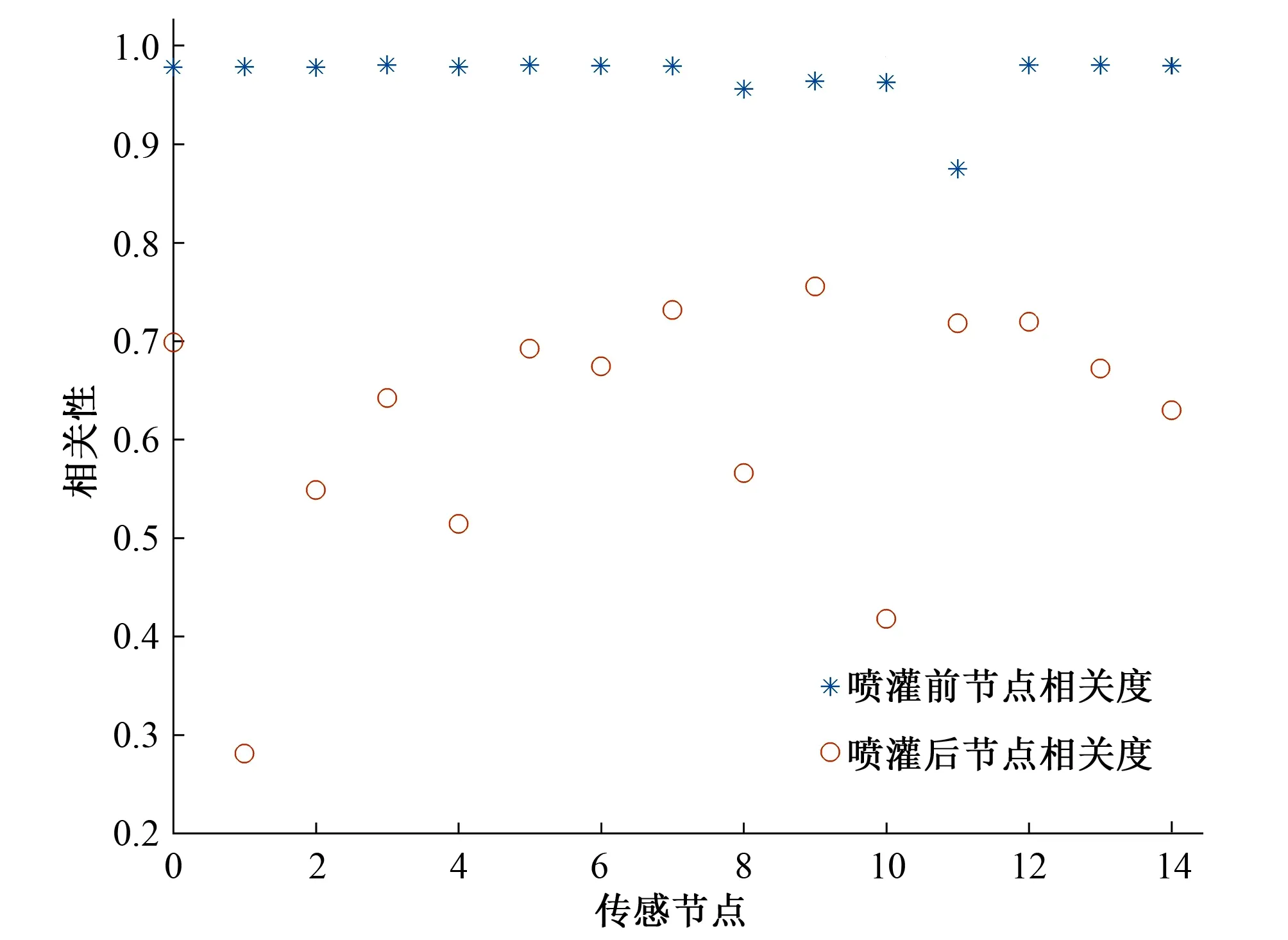
图1 微喷前后节点相关性图Fig.1 Node correlation diagram before and after micro-spray

由图1可以看出，由于微喷头的喷洒不均匀性、窗户开口大小等情况，导致微喷后空气湿度的空间变异性增加。微喷前使用单点传感器能够较好反应研究区域情况变化，但微喷后(空间变异大)仍然使用单点传感器监测会造成采集数据不精确，影响后续的工作处理。部署越多湿度传感器越好(理想情况)，但考虑到实际作物生长环境、传感器价格等因素，这种大量传感器部署是不科学的。因此有必要对微喷后空间空气湿度传感器数目与位置进行优化。

2 原理与算法

2.1 逐步累积法

逐步累积法[14]是选择最优的一个值(候选位置集合)加入初始测量位置中，不断的迭代至达到最优的数目为止。本文研究对象是温室中空气湿度，数据间的关联性可以用线性相关程度表示，故适应度函数用传感器测得的数据序列间的非相关系数设计。具体适应度函数如式(1)所示。

(1)

式中：φi={φ1,φ2,…,φn}与φj={φ1,φ2,…,φn}分别为不同传感器测得的两组同一属性值；cov(φi,φj)为两组属性值的协方差，计算如式(2)所示；δi与δj分别为相应的标准差，计算如式(3)所示。

cov(φi,φj)=E[φi-E(φi)]E[φj-E(j)]

(2)

(3)

逐步累积法的传感器配置优化是依次添加属性值最佳的传感器过程，具体步骤如下，第一步是传感器选择，以相关性最小为优化目标处理。第二步是矩阵降维，删除矩阵中最优传感器列的相关值。第三步是选择最佳传感器，在降维矩阵中不断循环选择最佳传感器。

2.2 离散粒子群法

粒子群算法[15](Particle Swarm Optimization,PSO)是一种求解优化问题算法。大部分应用是针对连续空间的问题寻优，但许多实际问题是组合优化问题。目前有两种常用的PSO结构，一种是改变离散问题表示方法，将其转换为连续空间的问题，仍然采用连续空间粒子群算法求解；另一种是改变粒子群结构，根据粒子群结构框架，重新定义问题的表示和速度-位置规则优化求解。

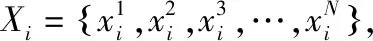
将经典粒子群速度-位置更新为新的公式，新速度-位置公式如下：

Vi(t+1)=w⊗Vi(t)⊕(c1r1)⊗(xi,pbest(t)-

xi(t))⊕(c2r2)⊗(xi,gbest(t)-xi(t))

(4)

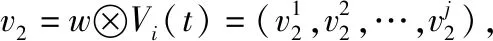
(5)

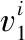
2.3 温室空气湿度传感器部署算法

温室空气湿度变化梯度较大和极值点的位置是我们部署传感器时需要特别注意的地方。为防止传输干扰的问题，传感器也不能部署太近。考虑上述因素，本文制定了温室空气湿度部署原则方案，具体步骤如下：

(1)温室空间的规则划分，立体规则网格的大小，需要结合实际温室范围和作物特性来确定。

(2)确保初步部署覆盖性，一般取立体规则网格中心、边中线点等具有代表性位置进行部署。

(3)测量初步部署传感器位置的空气湿度值。

(4)利用逐步累积法进一步优化传感器部署结构，得到较少传感器部署数目。

(5)构建新适应度函数，本文利用时空协同克里金插值函数[16]构建离散粒子群优化的适应度函数，具体如图2所示。

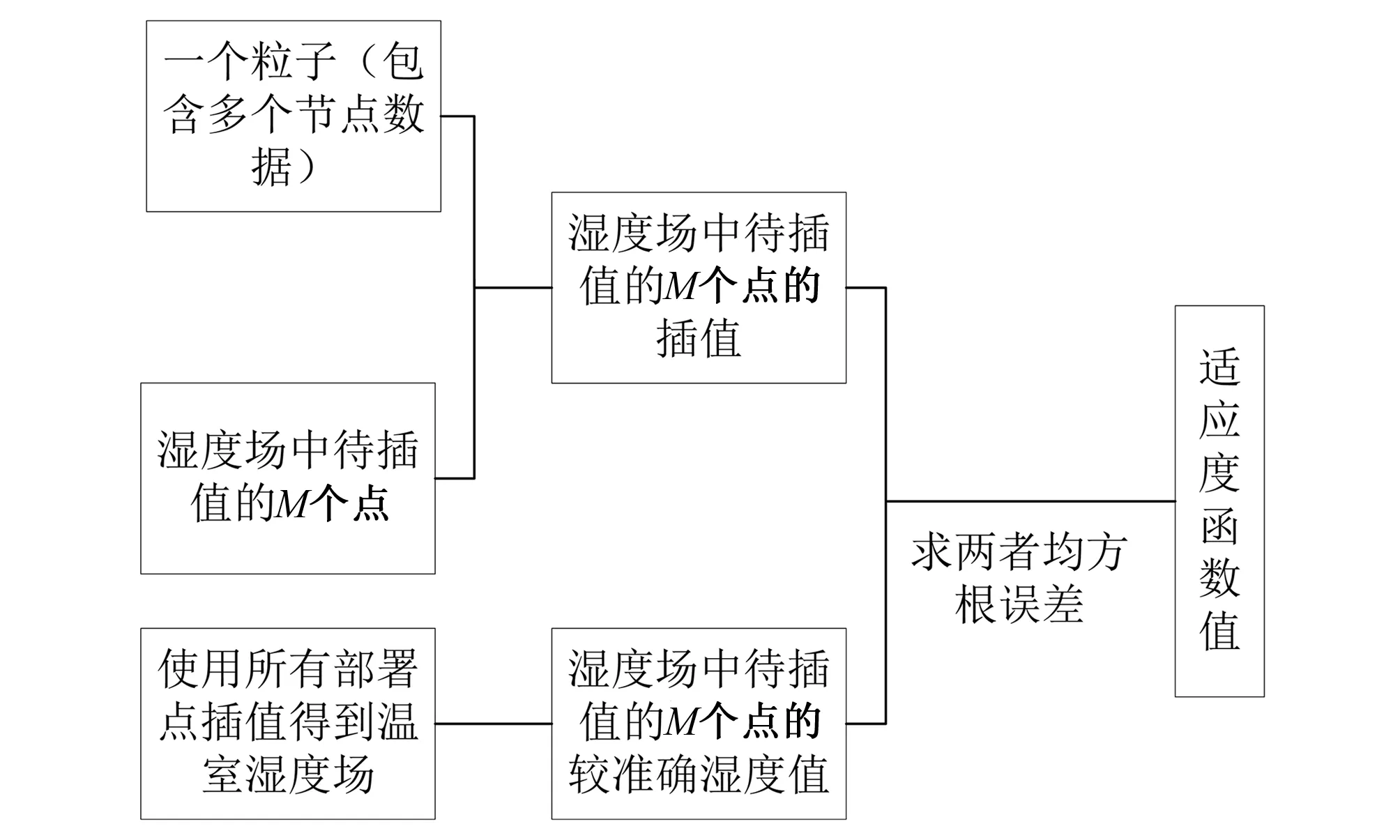
图2 新适应度函数构建图Fig.2 New fitness function construction graph

(6)利用离散粒子群算法优化传感器部署结构，通过新建的离散粒子群算法不断迭代得到更有代表性的传感器部署位置与数目。具体算法流程图如图3所示。

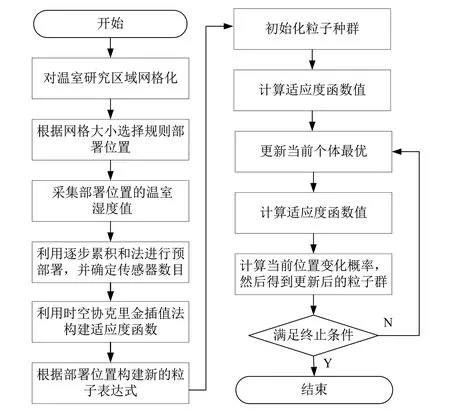
图3 传感器优化部署算法流程图Fig.3 Flow chart of sensor optimization deployment algorithm

3 仿真数据实验及分析

本文的实验是在西南科技大学生命学院实践基地的费约果幼苗扦插温室大棚进行实验的，将15个空气湿度传感器均匀分布在监测区域(微喷头下1 m3的空间)，具体如图4所示。

图4 传感器部署位置图Fig.4 Sensor deployment location map

平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE)[17]的定义为：

(6)

(7)

(8)

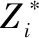
3.1 空气湿度传感器数目确定

利用温室空气湿度传感器采集的数据集，计算传感器间相关性，得到最佳空气湿度传感器组合。以最佳传感器相关性进行归一化，对空气湿度传感器排序，结果如表1所示。

本文以2号传感器数据为代表，显示传感器对温室湿度分布状态影响。首先将2号传感器测得数据定义为100%的有效度(即相关性与测量贡献度成反比)，然后将其余传感器数据进行归一化(参考2号传感器数据)，最后将部署的每个传感器有效度刻画到一幅图中，结果如图5所示。

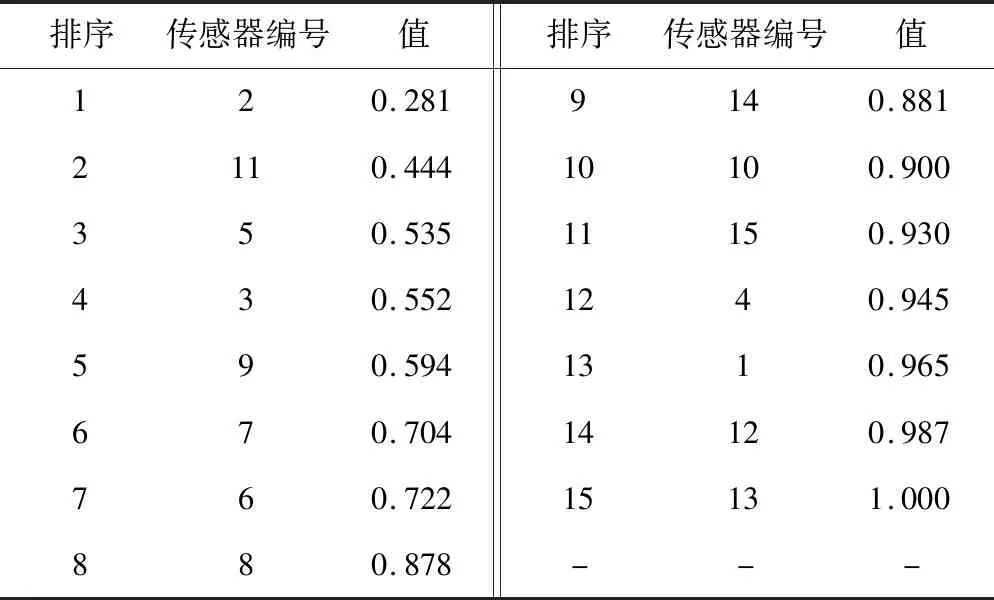
表1 规则部署传感器优化排序表Tab.1 Rule deployment sensors optimized sort table

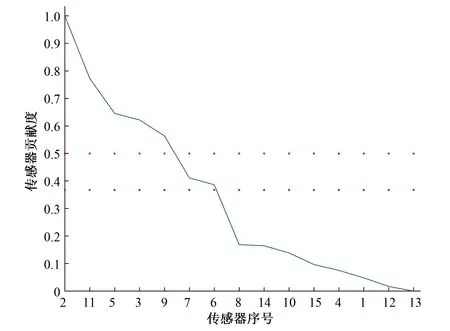
图5 规则部署传感器有效度Fig.5 Rule deployment sensor validity

由图5看出，基于平均下降方式(贡献度大于0.5)，前5个传感器对空气湿度模态贡献较大；基于自然对数下降方式[贡献度大于exp(-1)]，前7个传感器对湿度模态贡献较大。根据相关文献查阅和实际温室需求，一般将控制传感器数量在5～7个之间。

3.2 离散粒子群算法优化

本课题研究选择7个传感器进行部署(考虑到成本和实际的需求)，为了后续进行对比，故离散粒子群算法也以7个传感器部署进行优化。优化得到的离散粒子收敛结果，如图6所示，最小适应度函数值为0.305 1，部署传感器位置为：传感器2、3、5、8、10、11、12。

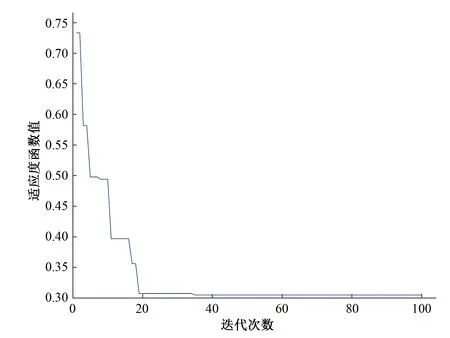
图6 离散粒子群优化结果Fig.6 Discrete particle swarm optimization results

3.3 两种算法优化结果对比

在统计方面，利用F检验(基于方差的显著性检验)和T检验(基于平均值差别的显著性检验)验证两种方法优化前后检测结果，如表2所示，结果显示两种方法没有显著性差异。

假设传感器测得的数据为实际真实数据，本研究首先以部署前测得的数据利用克里金插值进行重建，作为真实情况参考。然后分别对利用逐步累积法和离散粒子群算法优化的部署方案测得的数据进行空气湿度场插值重建，最后分别对重建三维空气湿度场图的多个方向切面对比结果，结果如图7所示。

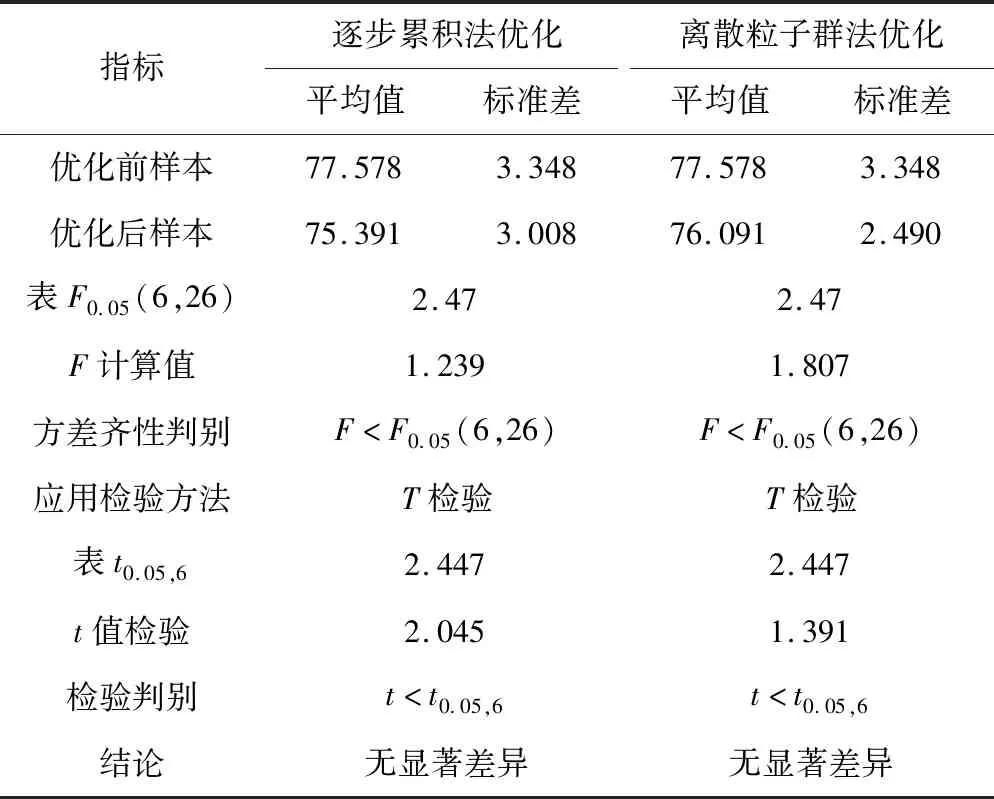
表2 两种方法在统计方面对比表Tab.2 Comparison of the two methods in terms of statistics

图7 3种情况下得到的空气湿度场重建图Fig.7 Air humidity field reconstruction map obtained in three cases

由图7插值结果可见，研究区域空气湿度场变化情况在两种方法中都能够得到很好地反映，但直观上看，离散粒子群优化的方案得到结果更贴近实际情况。为了更详细、数值化的比较结果，本文用3种不同评价指标比较了两种优化后部署情况，结果如表3所示。

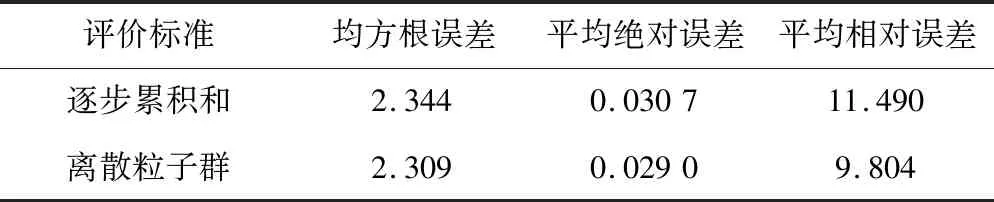
表3 两种优化结果在不同标准下对比Tab.3 Comparison of two optimization results under different standards

综合以上比较结果，表明本文针对温室空气湿度部署问题，重新设计的离散粒子群算法能够得到精确的温室空气湿度分布特征，为后续的温室控制研究提供精确的数据。

4 结 语

本文将设计的离散粒子群算法应用于温室空气湿度场重建，利用时空协同克里金插值方法建立适应度函数，以离散粒子群算法优化温室空气湿度传感器部署问题。在实验条件下，利用采集微喷前后温室湿度数据重建温室湿度场，实验结果表明：逐步累积法和离散粒子群法均能有效的求解温室湿度场重建问题，重建的湿度场能够准确反映出温室内微喷下湿度变化，实现温室中湿度场的可视化。通过统计方法和重建精度等评价指标衡量湿度场重建的质量，与逐步累积法相比，离散粒子群优化的部署方案具有更准确的优势。今后的研究可以将该部署方法应用于结构健康、传感节点部署等方案。