基于神经网络灰色模型的农田土壤湿度预测研究

王 冰 玉

(永城职业学院, 河南 永城 476600)

土壤湿度是旱涝评价的直观指标，对地表能量、降雨再分配、水资源管理、农业灌溉等方面都有重要影响。土壤湿度过低，形成土壤干旱；土壤湿度过高，恶化土壤通气性，影响田间耕作措施和播种质量，因此土壤湿度已成为农业、生态、气候、环境、水文、灾害等诸多领域的关键研究内容，准确预测土壤湿度情况有着重要的现实意义[1]。

目前研究方法主要有：仪器法和遥感测量等方法[2,3]，但是由于土壤湿度变化的复杂性和现场监测仪器的不确定性，监测数据的质量通常较差。经验模型[4]，虽然简单实用，但是模型中的参数适用范围有限。时间序列模型虽说有较好的适用性[5]，但是使用中所需的测量因素很多，且需要的数据量很大。水量平衡模型中有许多因素需要测量和计算[6]，如果缺少部分输入，模型的预测结果将产生较大的误差。土壤水动力学模型中参数的测量和计算比较困难[7]，阻碍了模型的实际应用。神经网络模型以各层土壤历史含水量为输入[8]，预测未来某一阶段土壤含水量的变化，但是当数据不充分的时候，神经网络就无法进行工作。灰色模型计算简单[9]，但适应性差，无法解决各因素之间的非线性关系。

本文将灰色模型与神经网络算法相结合，采用组合模型即神经网络灰色模型建立预测模型，通过利用关联度的计算，从而优化模型，提高模型的预测精度。

1 神经网络灰色模型

1.1 建立GM(1，1)灰色模型

(1)

GM(1，1) 累加数列拟合获得预测方程：

(2)

式中：a为发展灰数；u为内生控制灰数。

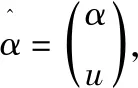
(3)

(4)

对微分方程的求解得预测方程：

(5)

通过反推数据即可获得原始数据序列的拟合值为：

(6)

1.2 神经网络模型

为了对灰色模型进行校正，采用神经网络模型。三层神经网络可以逼近任何非线性函数[11]，因此选用三层神经网络进行土壤湿度预测，即网络中除了输出层、输入层外，只有一个隐含层。模型选用土壤垂直深度为10、20、30、40、50、60 cm土壤含水量作为输入，60 cm的土壤含水量为输出，输入层包含6个神经元，输出层包含1个神经元。隐含层神经元数根据：

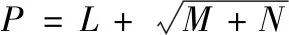
(7)

式中：M、P、N分别为输入层、隐含层和输出层神经元的数目，L∈[1,10]。

神经网络训练学习率值设为0.45；最大迭代次数为2 000；训练精度为0.001，经过反复调整隐含层的神经元个数来确定网络结构，最终隐含层神经元的数目确定为8。即网络结构为6-8-1三层结构。假设训练集包括m个样本模式，对第p个训练样本，神经单元j的输入总和记为apj，输出记为Opj，权值记为Wpj，则：

(8)

神经网络模型对误差进行计算，通过误差对网络中的权值进行更新，网络误差定义为：

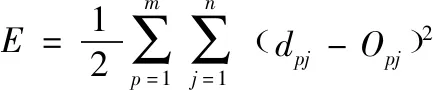
(9)

式中：dpj为第p个输入时输出单元j的期望输出。

设隐含层与输出层、输入层与隐含层的连接权值分别为ωpj和vpj，则其调整值为：

(10)

式中：η为学习率。

1.3 组合模型建立

(11)

式中：k=1,2,…,n。

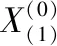
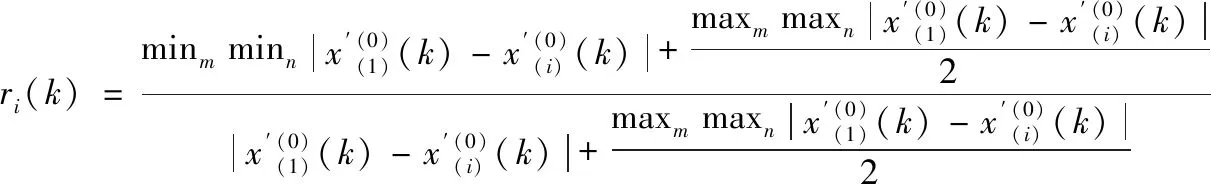
(12)

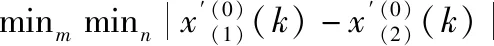
每个点的关联系数平均值作为参考序列和比较序列之间的关联度：

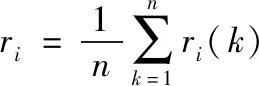
(13)

通过关联度对单个预测模型进行排序[12,13]，只对关联度值较大的单个预测模型进行组合预测，即设置阈值0.60，提取ri≥0.06的特性作为建模的变量。建立神经网络灰色组合模型：

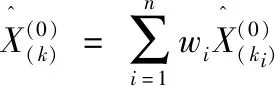
(14)

式中：wi为组合模型的权重系数，∑wi=1。

通过剩余预测偏差、判定系数指标判定模型的精度[14]，剩余预测偏差(Residual Predictive Deviation ，RPD)：

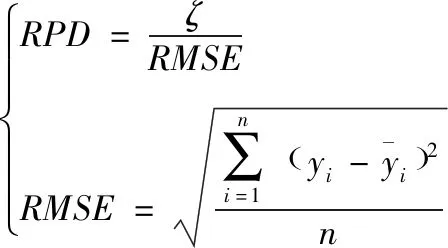
(15)

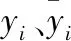
当RPD>2，模型预测能力比较强；2>RPD>1.4，模型预测能力属于中等水平；RPD<1.4，模型无法对数据进行预测。模型判定系数R2：

(16)

当R2越接近1时，表示模型的参考价值越高。①输入原始农田土壤湿度数据序列；②通过灰色模型获得预测数据； ③计算数据的关联度，把结果作为神经网络的输入样本值；④不断地修改各层的权重及阈值，使得网络误差函数逐渐减少，满足0.001，进行步骤⑤，否则进行步骤②；⑤输出预测结果。

2 实验仿真

实验采样仪器为SWR-2型土壤湿度传感器，实验地点设在国家级土壤监测点永城市双桥镇汤楼村，其土壤为砂姜黑土，土体深厚，年平均气温14.3 ℃，年平均降雨量874.3 mm，年平均日照时数2 300.1 h，年均太阳辐射量117.7 kCal/cm2，传感器的埋设位置是垂直地表下10、20、30、40、50、60 cm共计6个深度，利用Matlab7.0实现编程，对采样数据样本进行仿真训练，以每个处理土层的土壤湿度数据为训练集，对垂直地表下70 cm和80 cm的土壤湿度进行预测。神经网络训练学习率值设为0.45；最大迭代次数为2 000；训练精度为0.000 1。

2.1 模型训练结果

对不同深度，各采集10 d的数据，为方便分析对农田土壤湿度实测数据归一化处理，其结果如表1所示。

输入神经网络灰色模型后，预测结果以及相对误差如图1所示。

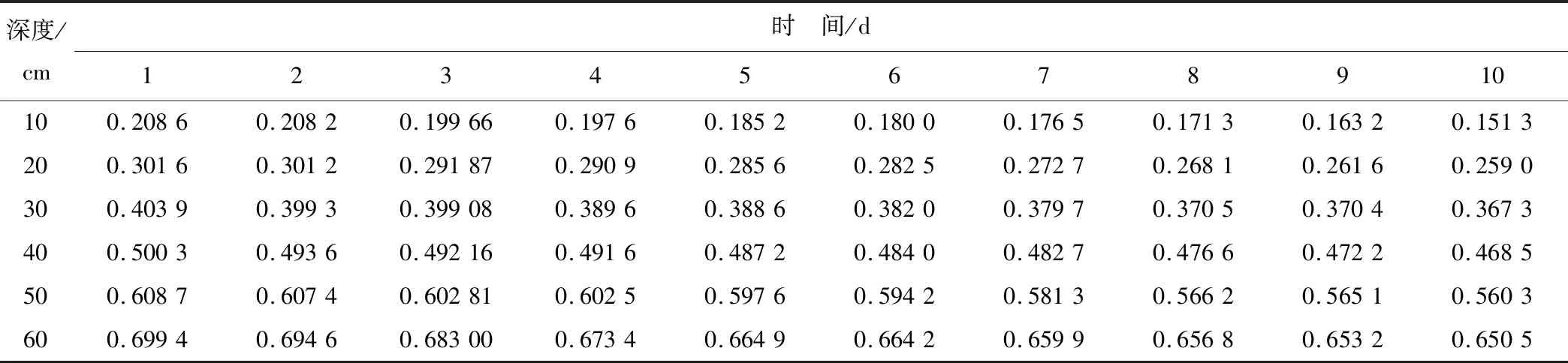
表1 农田土壤湿度数据归一化Tab.1 Normalization of farmland soil moisture data

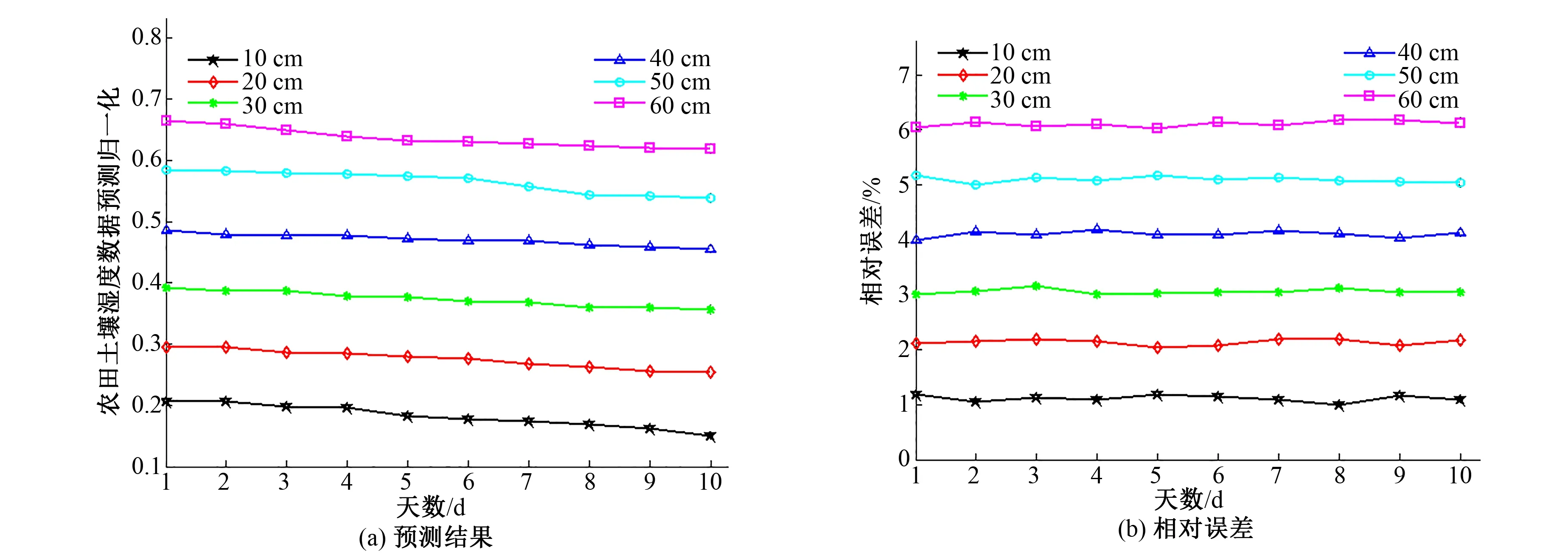
图1 农田土壤湿度数据预测结果以及相对误差Fig.1 Prediction results and relative errors of farmland soil moisture data

从图1可以看出，土壤湿度的预测值与实测值比较接近，随着农田土壤深度的增加，湿度数据预测值的相对误差也在增加，如深度在10 cm时相对误差最大为1.08%，深度在20 cm时相对误差最大为2.10%，深度在30 cm时相对误差最大为3.07%，深度在40 cm时相对误差最大为4.11%，深度在50 cm时相对误差最大为5.09%，深度在60 cm时相对误差最大为6.13%，并且相对误差随着农田土壤深度增加其波动性也在增加，土壤越深不确定性因素越多越不容易预测。

2.2 模型对比分析

对垂直深度70和80 cm的土壤湿度通过不同的模型进行预测对比分析，涉及的模型有：时间序列模型、土壤水动力学模型、水量平衡模型、神经网络模型、灰色模型、神经网络灰色模型，结果如图2所示。

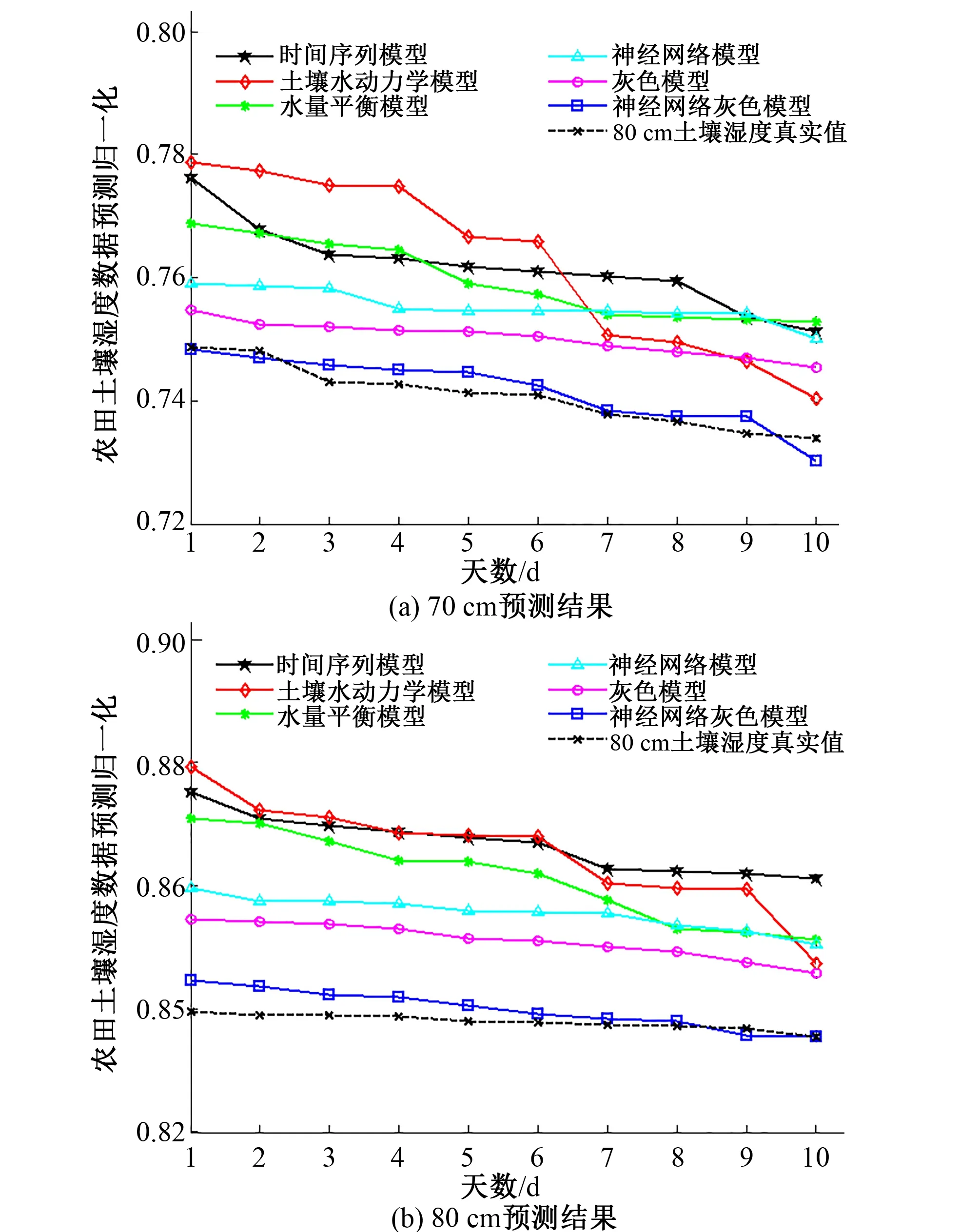
图2 模型预测对比分析Fig.2 Comparative analysis of model prediction

从图2模型预测对比分析可以看出，本文神经网络灰色模型对垂直深度70 cm和80 cm的土壤湿度预测值最接近真实值。

为了分析垂直深度70 cm土壤湿度不同模型预测的结果精度，进行剩余预测偏差RPD、模型判定系数R2指标分析，结果如图3所示。

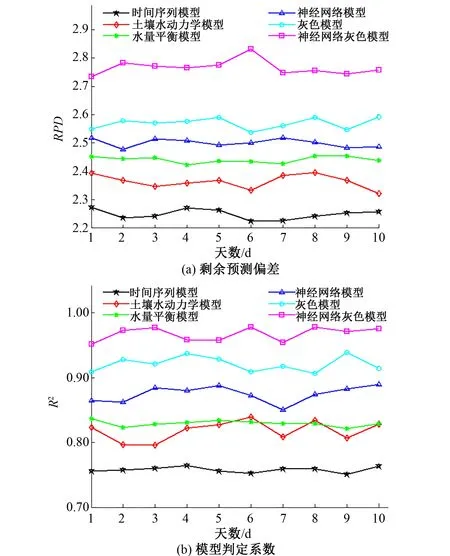
图3 对比分析指标Fig.3 comparative analysis indicators

从图3可以看出，各个模型RPD值都大于2，时间序列模型RPD最小值为2.22、平均值为2.27，土壤水动力学模型RPD最小值为2.31、平均值为2.38，水量平衡模型RPD最小值为2.41、平均值为2.437，神经网络模型RPD最小值为2.48、平均值为2.51，灰色模型RPD最小值为2.53、平均值为2.60，神经网络灰色模型RPD最小值为2.69、平均值为2.75，但是本文模型RPD值最大，模型预测能力比较强。本文神经网络灰色模型判定系数R2为0.98，最接近1，模型的参考价值最高。

3 结 语

本文提出神经网络灰色模型对农田土壤湿度预测，灰色模型对农田土壤湿度数据建模，神经网络对误差进行校正，神经网络灰色模型只对湿度数据关联度值较大的单个预测模型进行组合预测。实验结果表明本文模型对土壤湿度的预测值与实测值比较接近，但是预测值的相对误差随着深度的增加而增加，剩余预测偏差、模型判定系数指标值优于其他模型，因此为农田土壤湿度预测提供了一种新方法。