带缓冲区的设备预防维修策略研究

韩兆阳 严广乐 林数

摘要：为保证生产连续性，提出一种带缓冲区的两机设备预防维修决策模型。首先，根据系统周期内设备随机故障次数，计算系统周期内维修成本;然后，通过分析缓冲区库存变化，表达周期内缓冲区库存成本，同时在考虑维修成本和缓冲区成本的基础上，建立系统周期内总成本模型。最后，运用演化迭代算法求解出设备最优预防维修周期与最佳缓冲区库存。实际例证分析表明，该模型有效且可行。

关键词：缓冲区：预防维修;故障次数;成本

DOI： 10. 11907/rjdk.191277

开放科学（资源服务）标识码（OSID）：

中图分类号：TP319

文献标识码：A

文章编号：1672-7800（2020）001-0168-04

0 引言

隨着科学技术的不断进步，设备构造越来越趋向复杂化。设备在使用过程中不断磨损、劣化，存在安全、效率不确定等因素，一旦发生故障，生产线中断，将给企业带来严重的经济损失，所以对生产线设备进行预防性维护[1-3]成为降低制造业生产成本的重要因素。同时，在两级生产设备之间设置缓冲区，建立生产设备一缓冲区一生产设备的生产方式，在某种程度上能够缓解上游设备由于随机故障导致的生产中断[4-5]。在实际企业生产过程中，在两机设备之间设置一个库存缓冲区，使两机生产系统下的设备预防维修模型与实际生产制造系统更加吻合。

鉴于设备预防维护与缓冲区库存研究的应用价值，众多学者开展了一系列研究。Wijngaard[6]首次提出两机设备之间的库存缓冲区，运用随机模型对设备可靠性进行了深入研究，并针对缓冲区对生产系统产量的影响作出分析;Liao[7]通过分析设备在不同维护策略条件下对生产系统总运行成本的影响，建立了设备不同维修策略成本模型以确定最优维护周期;Chelbi&Ait_Kadi[8]假设上下游设备生产速率固定的前提下，通过建立上游设备的预防维修模型，求解出缓冲区最佳库存量;文献[9-10]针对带缓冲区的两机生产系统，假设上游设备失效时间服从指数分布，从而确定一个最佳缓冲区库存量，每当缓冲区库存达到额定库存量时，对上游设备进行预防维修;周炳海等[11-12]提出两机生产系统设备的预防维修方法，建立系统周期内生产总成本模型，通过演化算法，求解出最优维护周期;Salameh&Ghattas[13]基于准时制生产对设备进行定期预防性维护，建立缓冲区库存持有成本和缺货成本，并以此为目标函数，最终得到缓冲区库存最佳库存量;赵斐和刘学娟[14-15]针对仅含有两个部件的可修复系统，假设系统预防性维修后恢复至新的状态，运用时间延迟和更新理论方法，建立周期内预防维修成本模型，以周期内单位时间总成本最小化为目标获得最优预防维修周期;Dahane等[16]针对两机系统的生产计划产量，同时考虑了设备维护计划，提出了最大缓冲建模方法，但没有考虑缺货成本;周炳海和高忠顺[17]针对带缓冲区的生产系统，以预防维护时刻点为随机变量，建立周期内期望成本模型，通过构造算法求解出系统最优预防维修的时刻点。上述研究大多假设两机系统中的设备在每个预防维修周期末才发生故障，但在设备运转中，由于不确定因素的存在，使得设备随时可能发生故障，并且没有完全考虑系统整个周期内因设备故障带来的损失，所以模型精确度不高。本文同时考虑缓冲区库存变化对生产总成本的影响，建立两机系统设备预防维修模型，最终求解出设备最优预防维修周期及最佳缓冲区库存量。

1 问题描述

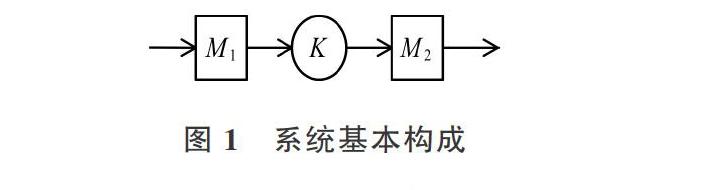
在两机生产系统中，中间设有库存量为K的缓冲区库存，上游设备M1为下游设备M2提供原材料或者半成品，如图1所示。

考虑设备故障对于缓冲区库存的影响，本文针对系统上游可修复设备M1建立等周期预防性维护，即在nT（n=1，2，3，…）个周期结束后对两机系统上游设备进行预防性维修。在两机生产系统中，系统上游设备M1以最大速率6（进行产品生产，系统下游设备M2始终以固定速率β从缓冲区夺取半成品，当缓冲区达到额定库存量K后，上游设备M的速率恢复至β，一直到本周期结束。为保证生产线的连续性，假设缓冲库存量能够支撑在上游设备预防维修时下游设备的连续生产。

由图1可知，为了确定M1的最优预防维护周期T*及最佳缓冲库存量、更加清晰地描述模型，进行以下假设：

（1）M2不会发生故障，一直处于正常运行生产状态。

（2）M1维修后恢复到最初全新的状态，即完美维护。

（3）在两机生产系统中，若上游设备发生故障，则采用事后维修。

（4）上游设备生产速率足够大，缓冲区库存量可快速达到额定值，T≥K/a。

（5）f（x）表示系统中上游设备预防性维修时间概率密度函数，h（x）表示维修时间概率密度函数，g（x）表示设备寿命概率密度函数，C为周期T内的总成本，Ch为周期T内的缓冲持有成本，Cm为周期T内的维护成本，Cp为周期T内运行成本，Cs为周期T内的缺货惩罚成本，Ccm为设备M1单位时间事后维修费用，Cpm为设备M1单位时间内预防性维修费用，Cth为缓冲区每个半成品单位时间的持有成本，Cts为单位时间缺货惩罚成本，Cα，Cβ为当系统设备以速率a或速率β运行时的单位时间运行成本，N为周期T内上游设备的的平均故障次数，MTBF为设备平均运行时间，MTTR为设备平均故障修复时间，Tpm为设备Mi预防维护的平均时间。

基于以上假设，本文通过建立两机生产系统总成本模型，在保证系统总成本最小化的前提下，找到最优预防性维护周期T*与最佳缓冲库存量K*。

以系统运行的单个周期为研究对象，其构成系统总成本函数中包括设备故障维修与预防维修成本、缓冲库存持有成本、系统下游设备缺货惩罚成本以及系统运行成本。其中缓冲区库存变化轨迹如图2所示。

1.3 缺货惩罚成本Cs

由于系統上游设备M，维护可能使缓冲区内缓冲库存为零，这时下游设备M2无法从缓冲区内获取半成品进行生产，致使缺货成本产生。

本文两机系统总成本模型旨在找出总成本最小时设备最优预防性维护周期T*与最佳缓冲库存量K*，同时找到缓冲区最佳缓冲库存量与预防性维护周期的对应关系，从而在实际生产中，更好地进行设备预防性维护。

2 模型求解

从目标函数可知，该两级生产系统预防性维护模型是一个相对复杂的积分表达式，对表达式进行多次求导后依然存在自变量，且不能判断目标函数的单调性，所以用常规的求导方法不能得到理想的最优解。为此，本文采用离散迭代法[19-20j求解每个变量对应的目标值，即对随机变量T按一定的步长逐一赋值。最后，把对应的目标值进行比较，找出其中最小值。

在模型求解前，需要根据实际工作经验确定预防性维护周期的上下限，即最大预防性维护周期T max和最小预防性维护周期T min。其中步长AT、AK可根据设备自身特性和实际生产情况确定。具体算法流程如图3所示。

求解最优预防维护周期T*和最佳缓冲区库存K*的算法描述如下：

3 实例分析

根据上述离散迭代算法，利用Matlab编程，计算结果如表1所示。

由表1可知，当T取0.2时，系统总成本最小，即0.2个月进行一次预防性维护，缓冲区最佳库存为192个。

通过对数值结果进行分析，可以看出在不同的预防性维护间隔期内，系统总生产成本会有浮动，企业可根据本文模型计算出适合自身的设备预防性维护间隔期和缓冲区最佳缓冲库存，防止设备故障引起生产停滞。

4 结语

本文针对两机生产系统，提出了一种同时考虑设备预防维修与缓冲区库存的预防维修模型。通过分析缓冲区库存变化对总生产成本的影响，建立了包括缓冲区库存持有成本、设备故障维修与预防维修成本、系统运行成本以及因设备故障造成缓冲区缺货成本的系统总成本模型，并利用演化迭代算法对该模型进行优化，求解定期预防性维护周期T和缓冲区最佳缓冲库存K这两个决策变量。数值结果表明，利用本文建立的两机生产系统预防维修优化模型能让系统作出最优维护决策，且可确定最优预防性维护周期与最佳缓冲区库存。但本文仅考虑了上游设备发生故障时的预防维修模型，对于上、下游设备同时发生故障的工作还有待进一步研究。

参考文献

[1]

BARLOW R E ， PROSCHAN F. Mathematical theory of reliahility [ M ] .New York ： John Wiley and Sons， 1965.

[2]

NAKAGAWA T. A summary of periodic replacement with minimal re-pair at failure [ J]. Journal of the Operations Research Society ， 1981 ， 24（ 3） ： 213-218.

[3]

NAKACAWA T. Periodic replacement models with threshold levels[J] . IEEE Transactions of Reliability ， 1991 ， 40（ 3） ： 395-397.

[4]

PAVITSOS A ， KYRIAKIDIS E C. Markov decision models for the opti-mal maintenance of a production unit with an upstream buffer [J].Computers & Operations Research ， 2009 ， 36（ 6） ： 1993-2006.

[5]

DUYN S F A， VANNESTE S G. Maintenance optimization of a produc-tion system with buffer capacity [J]. European Journal of OperationalResearch， 1995， 82（2） ： 323-338.

[6]

WIJINGAARD J. The effect of inter-stage buffer storage on the outputof two unreliable production units in series， with different production rates[ Jl. AIIE Transactions ， 1979 ， I l （ I ） ： 42-47.

[7]

LIAO C L. Optimum policy for a production system with major repairand preventive maintenance[J]. Applied Mathematical Modelling，2012， 36（ 11）： 5408-5417.

[8]

CHCLBI A. AIT-KADI D.Analysis of a production/inventory systemwith randomly failing production unit submitted to regular preventivemaintenance[J]. European Journal of Operational Research， 2001，156（3）：712-718.

[9]

MELLER R D，KIM D S.The impact of preventive maintenance on sys-tem cost and huffer size [J]. European Journal of Operational Re-search， 1996，95（3）：577-591.

[10]

KARAMATSOUKIS E U. DIMITRAKOS T D.Optimal preventivemaintenance of a production system with an intermediate buffer[J].European Journal of Operational Research， 2006， 168（1）：86-99.

[11] 周炳海，刘子龙.考虑质量损失的退化系统维护建模[J].浙江大学学报：工学版，2016. 12（ 50）：2270-2276.

[12]周炳海，高忠顺.带缓冲区的设备预防性维护优化建模[J].计算机集成制造系统，2012，18（2）：364-368.

[13] SALAMEH M K. CHATTAS R E.Optimal just-in-time buffer inven-tory for regular preventive maintenance [J]. International Journal ofProduction Economics. 2001. 74： 157-161.

[14]赵斐，刘学娟。两部件可修复系统预防性维修的策略模型[J].统计与决策，2016，（2）：52-55.

[15] 高胜，杨宏兵，倪婧，生产调度与预防性维护集成优化[J].组合机床与自动化加工技术，2018，（ 7）：169-173.

[16]

DAHANE M，CLEMENTZ C. REZC N.Effects of extension of sub-contracting on a production system in a joint maintenance and pro-duction context [J]. Computers and Industrial Engineering， 2010， 58（1）：88-96.

[17]周炳海，高忠順.带缓冲区的设备预防性维护优化建模[J].计算机集成制造系统，2012，18（2）：364-368.

[18]陆志强，王佳跃，周炳海.带缓冲区的可修复设备多目标预防性维护决策模型[J].计算机集成制造系统，2010. 16（10）：2124-2128.

[19] 余佳迪，周炳海.带缓冲的串行生产系统预防性维修策略[Jl.上海交通大学学报，2014，48（12）：1694-1699.

[20]刘勤明，吕文元，叶春明，考虑中间缓冲区的设备不完美预防维修策略研究[J].计算机应用研究，2018，35（9）：2614-2616.

（责任编辑：江艳）

基金项目：上海高原学科建设项目管理科学与工程项目（10-17-303-004）

作者简介：韩兆阳（1993-），男，上海理工大学管理学院硕士研究生，研究方向为作业车间调度;严广乐（1957-），男，博士，上海理工大学管理学院教授，研究方向为复杂系统理论与应用;林数（1992-），男，上海理工大学管理学院硕士研究生，研究方向为设备维修。