q 阶区间 orthopair 模糊 power 平均算子及其应用

司雅雪

摘要：将 power 平均算子推广至 q 阶区间 orthopair 模糊环境，提出一种 q 阶区间 orthopair 模糊 power 平均（q-RIVOFPA）算子并研究其性质。同时，给出一种基于 q-RIVOFPA 算子的模糊多属性决策方法，并通过实例验证其可行性和有效性。

关键词：q 阶区间 orthopair 模糊集;q 阶区间 orthopair 模糊 power 平均算子;多属性决策

Abstract： Power averaging operator is extended to q-rung interval-value orthopair fuzzy environment， and a q-rung interval-value orthopair fuzzy power averaging operator is proposed. Likewise， some properties of the aggregation operator are studied. Meanwhile， the fuzzy multi-attribute decision making method based on q-RIVOFPA operator is given， and its feasibility and validity are verified by the example.

Key words： q-rung interval-value orthopair fuzzy set;q-rung interval-value orthopair fuzzy power averaging operator;multiple attribute decision making

0  引言

多属性决策是根据不同方案的属性值对有限方案进行排序的过程，它在人们的日常生活和经营管理中有着重要作用。由于决策问题的复杂性和决策环境的模糊性，仅用精确值来表示备选方案的属性值是不够的。基于此，Zadeh[1]提出了模糊集理论。为针对不同的决策场景来描述对象的不确定性，Atanassov[2]于1983年提出了直觉模糊集的概念。作为扩展，Yager[3]提出了毕达哥拉斯模糊集，在该模糊环境下隶属度与非隶属度之和可以大于1，但其平方和不超过1。随着模糊集合的应用范围扩大，毕达哥拉斯模糊集仍存在局限性。为此，Yager[8-9]在直觉模糊集和毕达哥拉斯模糊集的基础上进行了拓展，提出了orthopair模糊集，其限制条件为隶属度与非隶属度的q次方之和不超过1，q？叟1。

通过引入各类集成算子，将信息进行综合处理，给决策分析带来了极大便利。为考虑所集结数据本身的重要程度，Yager在2001提出了Power平均（PA）算子[4]。随着研究的深入，Yager和Xu又将PA算子与几何平均结合，提出了Power几何平均（PGA）算子[5];姚平、陈华友和周礼刚将PA算子和调和平均相结合，提出了Power调和平均（PHA）算子[6];Xu和Cai将PA算子拓展至不确定环境下，定义了不确定Power平均（UPA）算子[7]。

目前，基于模糊环境下的信息集成算子及其应用成为了多属性决策领域的重要研究问题。通过与毕達哥拉斯模糊集的对比，Wei等[10]定义了orthopair模糊广义Heronian平均算子，并研究了其在多属性决策中的应用。然而，在实际决策中，属性值很难用一个精确值表示，决策者往往考虑用一个[0，1]的区间数表示[11-14]。为此，Wang，Gao，Wei和Wei[15]定义了区间值orthopair模糊集，其中隶属度和非隶属度都是[0，1]的区间数。Wang，Wei，Wang[16]等提出了q阶区间orthopair模糊麦克劳林对称平均（q-RIVOFMSM）算子，并研究其在多属性决策中的应用。

本文定义了q阶区间orthopair模糊power平均（q-RIVOFPA）算子，并探讨其幂等性、有界性和置换不变性。最后，研究q-RIVOFPA算子在多属性群决策中的应用，并验证该算子的可行性和有效性。

1  预备知识

下面将对基于q-RIVOFPA算子的多属性群决策实例进行分析。

例1.某顾客要对四辆不同品牌的汽车X={x1，x2，x3，x4，}进行选购，经三位专家商讨，最终以：价格（c1）、便利性（c2）、动力性（c3）和安全性（c4）这四个指标作为评判标准择优购买。

经三位专家评估，得到如表1决策矩阵。

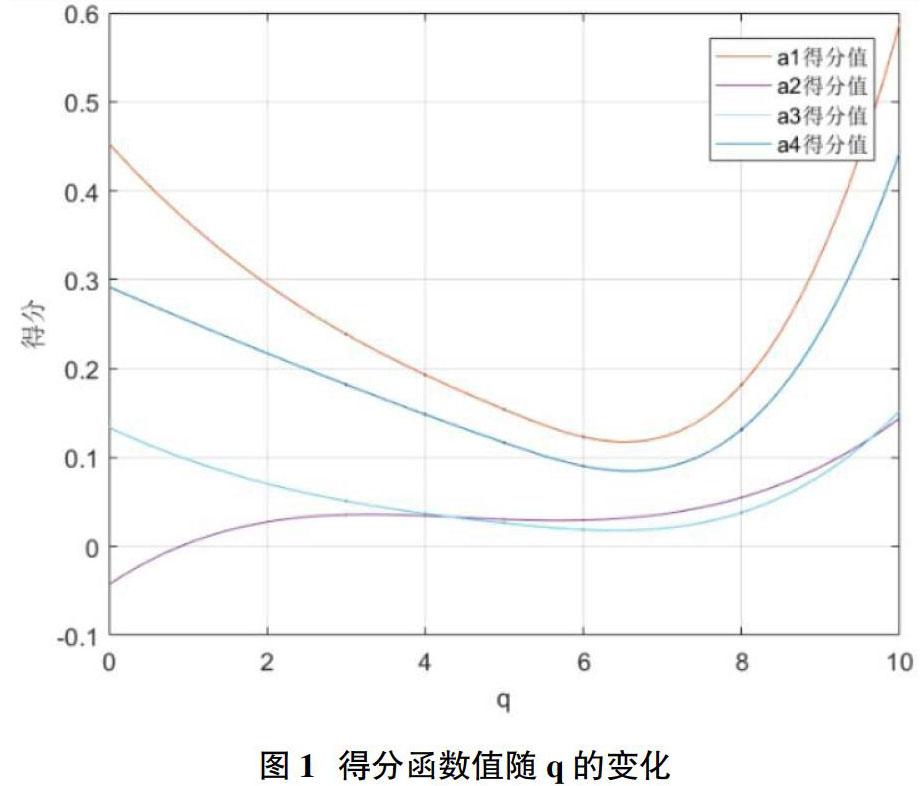
为了考虑阶数q对决策结果的影响，改变q的取值，分别得到相应的综合属性得分值S（ai），i=1，2，…，4，并绘制如图1图像。

由图可以看出，不论如何改变q的取值，综合属性值a1的得分都是最高的，即方案x1均为最优方案。

Wang[16]等提出了q阶区间orthopair模糊麦克劳林对称平均（q-RIVOFMSM）算子，利用该算子计算例1综合属性值ai的综合属性值排序为：

由上述结果可以看出，利用q-RIVOFPA算子和q-RIVOFMSM算子对四个方案进行排序，方案x2和x3的顺序有了变化，最优方案均为x1。与q-RIVOFMSM算子相比，q-RIVOFPA算子具有一定的优越性。q-RIVOFPA算子考虑了数据支撑度，可以帮助决策者更充分的利用数据信息，使决策结果更加客观合理。

4  总结

本文将power平均算子推广至q阶区间orthopair模糊集上，定义了q-RIVOFPA算子，并研究其幂等性、有界性和置换不变性。同时，给出了基于q-RIVOFPA算子的模糊多属性决策方法，并通过实例证明其有效性和可行性。未来，将进一步研究q-RIVOFPA算子的相关性质，并将其应用到风险分析、医药疗效、工业制造等其他不确定环境决策领域。

参考文献：

[1]Zadeh L A. Fuzzy sets[J]. Information and Control， 1965， 8（3）：338-353.

[2]Atanassov K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems， 1986， 20（1）： 87-96.

[3]Yager R. R.， Abbasov A. M. Pythagorean membership grades， complex numbers， and decision making[J]. International Journal of Intelligent Systems ， 2013， 28（5）： 436-452.

[4]Yager R. R. The power average operator[J]. IEEE Transactions on Systems， Man and Cybernetics-Part A， 2001， 31（6）： 724-731.

[5]Xu Z.S.， Yager R. R. Power-geometric operators and their use in group decision making[J]. IEEE Transactions on Fuzzy Systems， 2009， 18（1）： 94-105.

[6]姚平，陈华友，周礼刚.幂调和平均算子及其在模糊偏好关系群决策中的应用[J].运筹与管理，2012，21（5）：85-90.

[7]Xu Z.S.， Cai X.Q. Uncertain power average operators for aggregating interval fuzzy preference relations[J]. Group Decision and Negotiation， 2012， 21（3）： 381-397.

[8]Yager R. R. Generalized orthopair fuzzy sets[J]. IEEE Transactions on Fuzzy Systems， 2017， 25（5）： 1222-1230.

[9]Liu P.D.， Wang P. Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making[J]. International Journal of Intelligent Systems， 2018， 33（2）：259-280.

[10]Wei G.W.， Gao H.， Wei Y. Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making[J]. International Journal of Intelligent Systems， 2018， 33（7）： 1426-1458.

[11]Li Z.X.， Wei G.W.， Gao H. Methods for multiple attribute decision making with interval-valued pythagorean fuzzy information[J]. Mathematics， 2018， 6（11）： 228.

[12]Wei G.W.， Gao H.， Wang J.， Huang Y.H. Research on risk evaluation of enterprise human capital investment with interval-valued bipolar 2-tuple linguistic information[J]. IEEE Access， 2018， 6： 35697-35712.

[13]Wu L.P.， Wei G.W.， Gao H.， Wei Y. Some interval-valued intuitionistic fuzzy dombi hamy mean operators and their application for evaluating the elderly tourism service quality in tourism destination[J]. Mathematics， 2018， 6（12）： 294.

[14]Wang J.， Wei G.W.， Gao H. Approaches to multiple attribute decision making with interval-valued 2-tuple linguistic pythagorean fuzzy information[J]. Mathematics， 2018， 6（10）： 201.

[15]Wang J.， Gao H.， Wei G.W.， Wei Y. Methods for multiple-attribute group decision making with q-rung interval-valued orthopair fuzzy information and their applications to the selection of green suppliers[J]. Symmetry-Basel， 2019， 11（1）： 56.

[16]Wang J.， Wei G.， Wang R. Some q-rung interval-valued orthopair fuzzy Maclaurin symmetric mean operators and their applications to multiple attribute group decision making[J]. International Journal of Intelligent Systems， 2019， 34（11）： 2769-2806.

[17]李進军，包玉娥，李晨松.基于区间毕达哥拉斯模糊集的三类Hamming距离[J].湖北民族学院学报（自然科学版），2018， 36（4）：386-390.

[18]Liu P.D.， Chen S. M.， Wang P. The g-rung orthopair fuzzy power Maclaurin symmetric mean operators[C]. 2018 Tenth International Conference on Advanced Computational Intelligence （ICACI）. IEEE， 2018： 156-161.