基于场变换理论的大角度涡旋电磁波生成方法*
冯加林 施宏宇 † 王远 张安学 徐卓
1) (西安交通大学,多功能材料与结构教育部重点实验室,西安 710049)
2) (西安交通大学,电子与信息学部,西安 710049)
3) (西安交通大学,电子陶瓷与器件教育部重点实验室,西安 710049)
场变换是一种与入射角度无关的新型电磁变换方法,可对电磁波极化和阻抗进行调控.本文提出了一种基于场变换理论的大角度入射涡旋电磁波产生方法.基于该方法设计了一种用于涡旋电磁波生成的人工媒质,并通过对其仿真验证了所提出的方法.设计的人工媒质为多层环形结构,可以透射生成2阶涡旋电磁波,并且具有较好的入射角度稳定性,在60°斜入射时仍能产生涡旋电磁波.
1 引 言
电磁波携带能量和动量,动量可以分为线动量和角动量,其中角动量包括由偏振决定的自旋角动量 (spin angular momentum,SAM)和由光场空间分布决定的轨道角动量(orbital angular momentum,OAM)[1].自旋角动量与电磁波的极化有关.轨道角动量则描述了波前围绕电磁波传播方向所在轴的旋转,从而形成涡旋电磁波,单光子携带的轨道角动量表示为lℏ ,其中拓扑荷数l为任意整数,ℏ 为约化普朗克常数,不同的l代表了不同的OAM模态.l取值可以从负无穷到正无穷,不同的OAM态相互正交[2].将l作为调制参数,将不同的信息调制到不同模式的OAM涡旋波上可以实现在同一载频下拥有无穷多个相互独立的轨道角动量的信道,这对提升通信系统的信道容量有着重大意义.这种通信方法可应用在自由空间通信、光纤通信[2]和量子通信[3,4]中.此外,OAM波还在超分辨率图像[5]、光镊[6],数据存储[7]等领域有很大的潜力.
常规产生携带OAM的轨道角动量的方法有:螺旋相位板 (spiral phase plate,SPP)[8−10]、q 板[11]、计算全息法[12]、天线阵列[13]等,但有着加工难度大、尺寸较大、所生成的OAM模式单一或者转换率不高等缺点.近年来利用超表面可以使电磁波产生相位突变的特点产生OAM波已经成为研究热点,其中主要有基于谐振模式的超表面涡旋光束控制[14],基于几何相位调控的涡旋光束产生[15,16]和基于传输相位的涡旋光束[17]等方法.2016年,Yue等[18]利用几何相位的原理设计了一种理论上实现了接近100%效率的OAM反射超表面.Yang等[19]实现了平面波垂直入射和斜入射下OAM波的生成,但其斜入射的角度较小,为 18°.目前大多数的研究都集中在反射型生成OAM[19−21],基本上都是垂直或者小角度入射生成OAM波,所以在大角度入射情况下透射生成OAM波的问题亟待研究.
场变换 (field transformation,FT)方法是一种调控电磁波极化和阻抗的理论方法.它由麦克斯韦方程组和预设的边界条件推演而来,基于无源互易材料来控制电磁波传播[22,23],场变换方法与变换光学互补.变换光学用于调控电磁波波前,而场变换则用于调控电磁波极化和阻抗.值得一提的是,场变换能够在任意入射角度下控制每个电磁场分量阻抗和极化状态.因此,场变换方法被广泛用于波片[24,25]、极化器[26]和天线设计[27]等研究中.
本文利用场变换理论与等效媒质理论,提出了一种可在大角度入射下产生涡旋电磁波的方法,并设计了一种可以透射产生涡旋电磁波的人工媒质,通过数值仿真验证了所提方法的有效性.实现的人工媒质具有较好的入射波角度稳定性,在以60°的角度斜入射仍能生成2阶OAM电磁波,这种方法也可以实现生成任意阶次的OAM波[28].
2 理论分析与结构设计
2.1 场变换理论
场变换理论示意图如图1所示.根据场变换理论,对于一个在xoy平面传播的平面波,利用介质进行场变换的过程可以描述为[22]
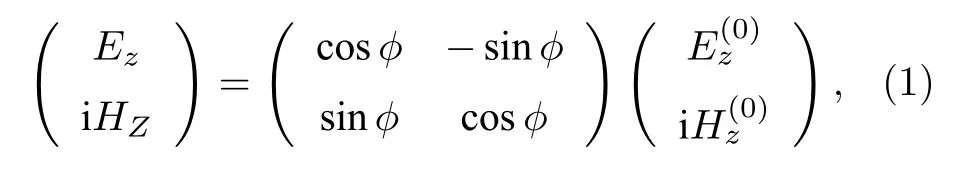
式中Ez为场变换后电场的z分量,Hz为场变换后磁场的z分量,为场变换前电场的z分量,为场变换前磁场的z分量,ϕ为场变换参数.
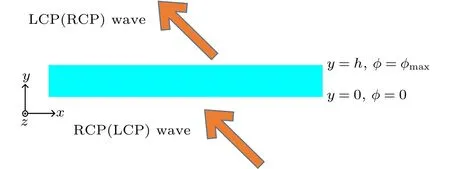
图1 场变换示意图Fig.1.Schematic diagram of the FT medium.
从(1)式可以看出,场变换理论上与入射角度无关,因此,理论上可以设计出对入射角度不敏感的媒质.当ϕ不为零时,通过场变换理论可以得出介质的介电常数张量和磁导率张量如下[19]:


式中A=Ay.但是在实际中,想得到满足(3)式的介电常数张量和磁导率张量十分困难,通过使用化简参数近似的方法可以将(3)式进一步化简[24,29]:



图2 人工双折射材料: xyz 轴绕 y 轴旋转 45°变成 x′yz′ ,入射波在 xy 平面内,θ 为入射角,k0 是入射波的波数Fig.2.Artificial birefringence medium: The xyz coordinate is twisted along the y -axis by 45° to the x′yz′ coordinate.The incident plane is x-y plane,θ is the incident angle,k0 is the wave vector of the incident wave.
利用等效介质理论计算出这两种介质叠加时的等效介电常数,该理论要求两种材料的厚度要远小于波长,等效介电常数为

2.2 结构设计
对于透射型的人工双折射介质,入射电磁波和透射电磁波的极化状态可以用琼斯矩阵J描述[31],当电磁波沿着z方向入射到人工双折射介质上,将电磁波按照圆极化分解:

其中Jc为圆极化分解时的琼斯矩阵,J++为右旋圆极化分量电场的同极化转化效率;J+−为右旋圆极化分量电场的交叉极化转化效率;J−+为左旋圆极化分量电场的交叉极化转化效率;J−−为左旋圆极化分量电场的同极化转化效率;Jxx为x方向极化分量电场的同极化转化效率;Jxy为x方向极化分量电场的交叉极化转化效率;Jyy为y方向极化分量电场的同极化转化效率;Jyx为y方向极化分量电场的交叉极化转化效率.当Jxx=−Jyy=1 且Jxy=Jyx时,以入射法线方向为轴将该反射体旋转a角,此时线极化的琼斯矩阵变为
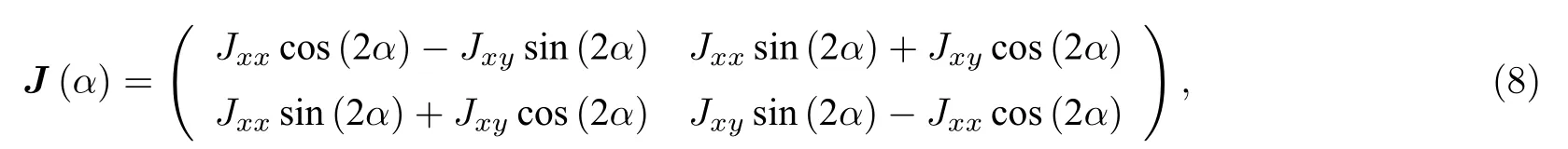
圆极化琼斯矩阵变为

当Jxy=Jyx=0 时,此时 (8)式和 (9)式变为

此时琼斯矩阵变成对角矩阵,可以将其等效为半波片的琼斯矩阵,这意味着左旋圆极化(右旋圆极化)在透射后成为右旋圆极化(左旋圆极化).同时,引入了一个统一的相位系数 e±2iα,称为Pancharatnam-Berry相位,也被称为几何相位[32].
如图3所示,当入射波沿着y方向入射到图2中的人工双折射材料单元上时,将单元绕y轴旋转角度α,可以引起 2α的相位改变.为了产生 OAM,几何相位被用于构建OAM定义要求的相位轮廓eilϕ.因此为实现l模式的OAM波,单元需要被设计为有lϕ的相位改变,即α=±lϕ/2.符号取决于入射圆极化波的极化状态.当Jxx=−Jyy=±1 ,Jxy=Jyx=0时,可以实现 OAM波的生成[31].根据以上的理论分析,最终设计出的单元如图4所示.

图3 Pancharatnam-Berry(几何)相位,入射波沿 y 方向照射到单元上,单元绕y轴旋转 α ,带来 2 α 的相位变化Fig.3.Pancharatnam-Berry phase: When the EM wave incident on the unit along y direction,and the unit rotates α around the y axis,the phase changed 2 α.

图4 单元模型Fig.4.The model of unit cell.
单元模型由两种介质组成,红色部分介质为Arlon1000,其介电常数为 10,蓝色部分介质为介电常数为1.14的泡沫,两种介质的损耗角正切分别为0.0023和0.00877,厚度分别为0.5和3.5 mm,在x方向的长度为 10 mm,z方向的长度为30 mm.电磁波沿着z方向入射到单元上,经过仿真得到该单元Jxx,Jyy的幅度如图5(a) 所示,Jxx和Jyy的相位如图5(b)所示,在 12.75 GHz时,Jxx与Jyy的 相 位 差 为 180°,故 该 模 型 可 以 在12.75 GHz附近实现几何相位.
Jxy和Jyx的幅度如图6 所示.可见Jxy和Jyx的幅度都低于–80 dB,接近于 0.从以上的仿真结果可知,单元满足Jxx和Jyy的幅度相等且相位相反,Jxy和Jyx的幅度都接近为 0.
将上述单元绕波的入射方向即z方向旋转成圆环状,即旋转360°,根据对几何相位的分析可知,可以引起720° 的相位变化.最终旋转得到的圆环如图7 所示,其半径为 200 mm,一共有 100 个介质圆环.
3 仿真结果与分析
在仿真圆环时使用左旋圆极化的高斯波束沿着z方向入射到介质圆环的上方,穿过圆盘后透射到介质圆环的下方.高斯波束的束腰距离介质圆环的表面为 188 mm,束腰半径为 60 mm,当高斯波束垂直入射时,在13 GHz时的透射波中右旋圆极化分量的电场幅度和相位如图8所示.
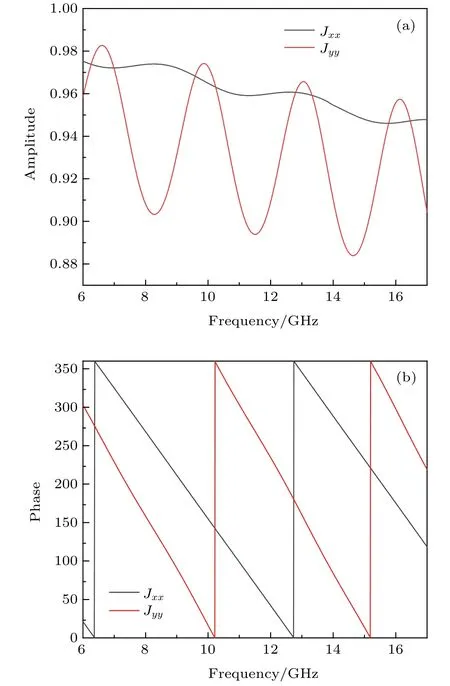
图5 (a) Jxx 和 Jyy 的幅度 ;(b) Jxx 和 Jyy 的相位Fig.5.(a) The amplitude of Jxx and Jyy ;(b) the phase of Jxx and Jyy.
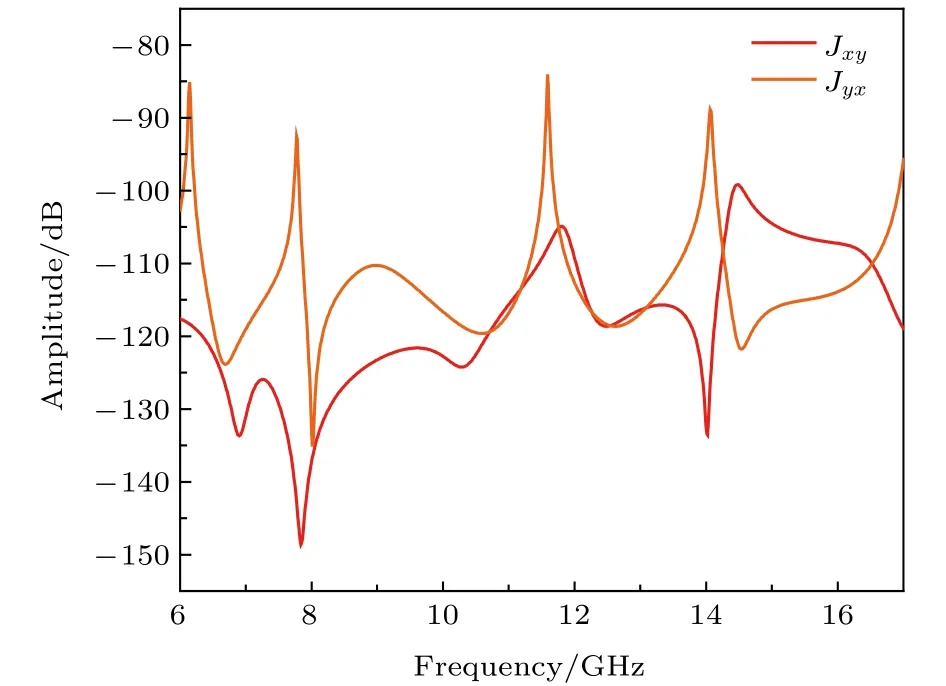
图6 Jxy 和 Jyx 的幅度Fig.6.The amplitude of Jxy and Jyx.
图8(b)给出了此时在介质圆环周围的电场分布.由于相位奇点的存在,右旋圆极化波分量的中心位置幅度非常小(如图8(c)所示),而能量集中在圆环状区域中.相位如图8(d)所示,可见相位从0变化到了 4π ,成涡旋状,因此可见右旋圆极化分量作为交叉极化分量携带了2模式的OAM,该模型的转化效率非常高.表1列出了不同频点右旋分量的最大值.可见该模型的带宽比较宽,在11—15 GHz内均可较高效率地产生OAM波.

图7 (a)旋转所形成的介质圆环的主视图,由100个圆环组成每个圆环的半径为4 mm;(b)介质圆环的侧视图Fig.7.(a) Main view of dielectric rings,it’s consists of 100 rings with radius of 4 mm and thickness of dielectric rings is 30 mm;(b) side view of dielectric rings.
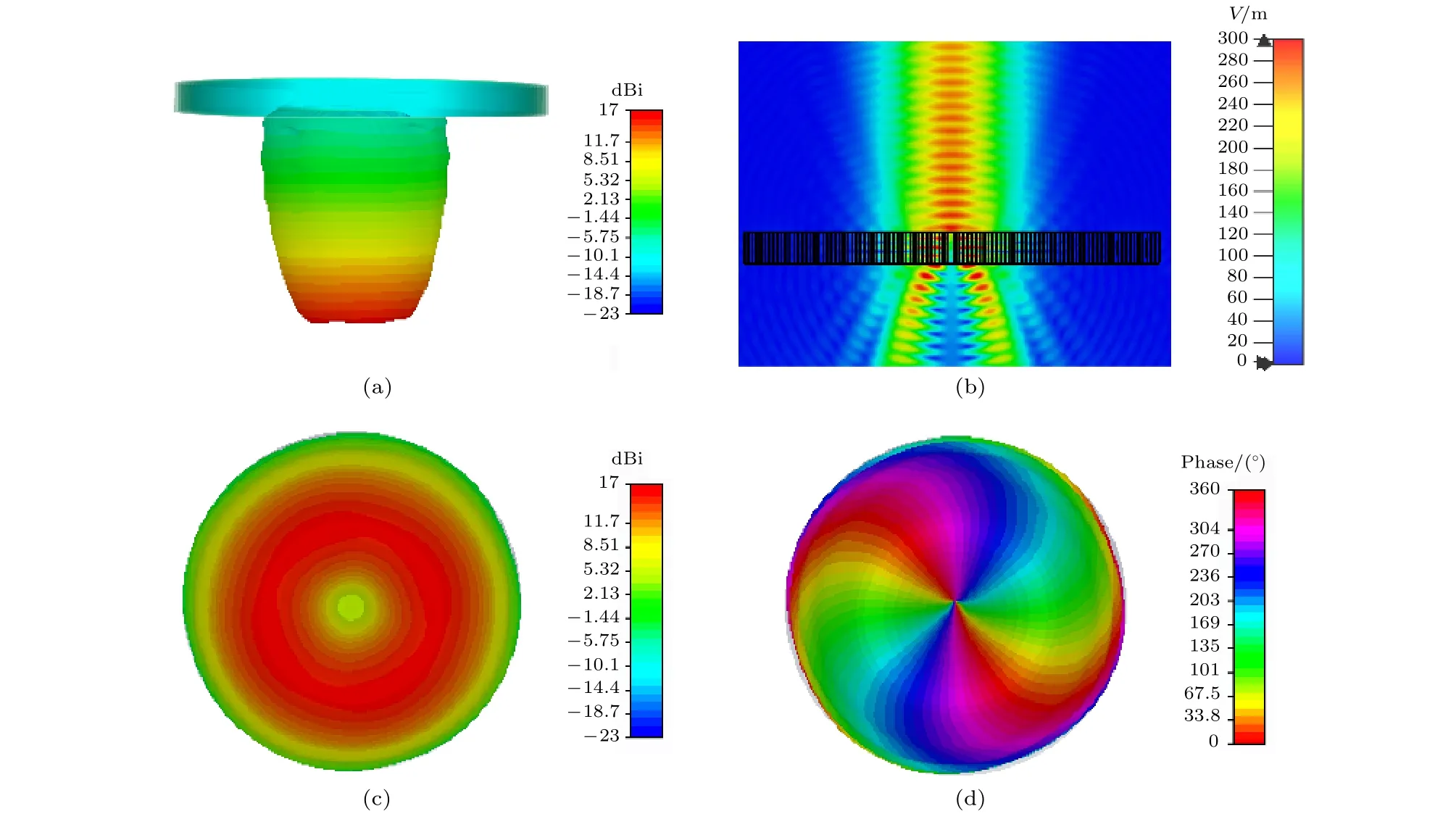
图8 (a)垂直入射的透射波;(b)介质圆环周围空间的电场分布;(c)13 GHz 时右旋圆极化波的幅度;(d)13 GHz 时右旋圆极化波的相位Fig.8.(a) The transmission wave while incident angle is 0°;(b) E-field distribution around dielectric rings;(c) amplitude of RCP wave at 13 GHz ;(d) phase of RCP wave at 13 GHz.
改变高斯波束的入射角度,当20°斜入射时,13 GHz时透射波的右旋圆极化分量的电场幅度和相位如图9所示.其中介质圆环的电场如图9(b)所示,可见在20°斜入射时有一部分高斯波束在圆环的上方被反射,透射电磁波仍然具有明显的相位极点,右旋圆极化波电场能量分布依然为圆环状.右旋圆极化波的幅度分布为圆环形,中心的相位奇点非常明显,中心幅度非常小,圆环处幅度比较大,为 17.2 dBi,其转换效率仍然较高.如图9(d)所示,相位呈螺旋状,从 0 变化到了 720°,所以透射电磁波的右旋圆极化分量仍然携带了2模式的OAM波.表2列出了20°斜入射时不同频点右旋分量的最大值.

表1 垂直入射时不同频点的右旋分量的最大值Table 1.Maximum values of RCP at different frequencies when normal incidence.

图9 (a) 20°斜入射时的透射波;(b) 介质圆环周围空间的电场分布;(c) 20°斜入射时 13 GHz 的右旋圆极化波的幅度;(c) 20°斜入射时在13 GHz的右旋圆极化波的相位Fig.9.(a) The transmission wave while incident angle is 20°;(b) E-field distribution around dielectric rings;(c) amplitude of RCP wave at 20° oblique incidence;(d) phase of RCP wave at 20° oblique incidence.
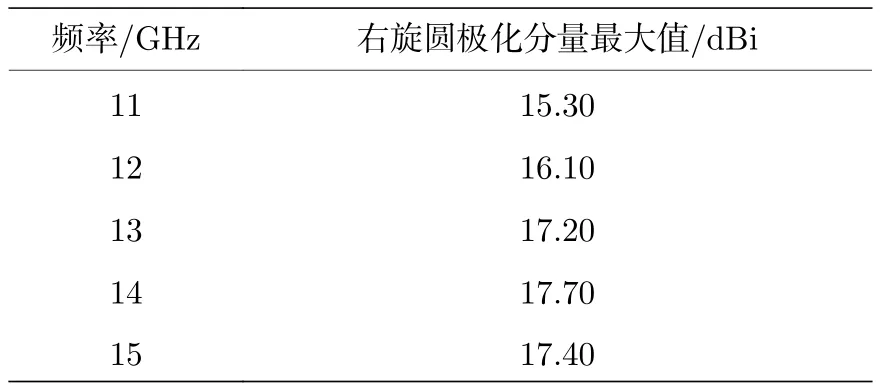
表2 20°斜入射时不同频点的右旋分量的最大值Table 2.Maximum values of RCP at different frequencies when incident angle is 20°.
该模型在20°斜入射时,产生的透射电磁波的交叉极化分量中携带了2模式的OAM,并且在13 GHz时转化效率很高,其右旋圆极化分量为17.2 dBi,在 14 GHz 时右旋圆极化分量为 17.7 dBi,14 GHz时右旋圆极化分量大于13 GHz时的右旋圆极化分量,由此可见中心频率变为 14 GHz,带宽较宽.相比垂直入射,性能基本没有变化.
当入射角度为 40°时,13 GHz 时透射波的右旋圆极化分量的电场幅度和相位如图10所示.其中介质圆环周围空间的电场分布如图10(b)所示,能明显观察到反射波束的电场;透射电磁波的右旋圆极化分量的幅度如图10(c)所示,有明显的相位奇点,中心位置幅度很小,但是最大值分布位置相比垂直入射时有变化,最大值为 17.4 dBi,转换效率很好;相位分布如图10(d)所示,相位依然是从0变化到了 4π ,呈螺旋状,证明右旋圆极化分量为2模式的OAM波,然而相比于垂直入射的情况,分布不再均匀.
表3给出了入射角为40°时不同频点右旋分量的最大值.入射角为 40°时,能够在 13 GHz 时较高效率地转化产生OAM波,且OAM模式为2.在13 GHz 时右旋圆极化分量为 17.4 dBi,在 14 GHz时右旋圆极化分量为 18.6 dBi,14 GHz 时右旋圆极化波的幅度大于13 GHz时右旋圆极化波的幅度,相比垂直入射,中心频率也变为 14 GHz,效率有一定的下降,转化出OAM波的效果也不如垂直入射时效果好.

图10 (a) 40°斜入射时的透射波;(b) 介质圆环周围空间的电场分布;(c) 40°斜入射时 13 GHz 的右旋圆极化波的幅度;(d) 40°斜入射时13 GHz的右旋圆极化波的相位Fig.10.(a) The transmission wave while incident angle is 40°;(b) E-field distribution around dielectric rings;(c) amplitude of RCP wave at 40° oblique incidence;(d) phase of RCP wave at 40° oblique incidence.

表3 40°斜入射时不同频点右旋分量的最大值Table 3.Maximum values of RCP at different frequencies when incident angle is 40°.
当波束的入射角为 50°时,13 GHz 的透射右旋圆极化分量的电场幅度和相位如图11所示.当波束的入射角为50°时,此时模型周围空间的电场分布如图11(b)所示,透射电磁波的右旋圆极化分量的幅度如图11(c)所示,可以看到携带2模式OAM波的右旋圆极化分量的幅度最大值分布在两个圆环上,其携带的2模式OAM波不纯,有两个相位奇点.在13 GHz这一频率该模型的转化效率有所下降.相位分布如图11(d)所示,绕该透射电磁波一周相位有 4π 的变化,但相位奇点非常明显地分成了两个,且相位分别不均匀,此时携带的2模式OAM不纯净.
表4列出了50°斜入射时不同频点的右旋分量的最大值.可知50°斜入射时,该模型可以转化入射的圆极化电磁波为交叉极化的OAM波,但转换效率与前面的情况相比下降明显,反射分量更大,转化的中心频率向高频移动,但此时仍能产生2模式的OAM波.

表4 50°斜入射时不同频点的左旋和右旋分量的最大值Table 4.Maximum values of RCP at different frequencies when incident angle is 50°.
当高斯波束以 60°角入射时,13 GHz 时透射右旋圆极化分量的电场幅度和相位如图12所示.其中图12(b)给出了60°入射时介质圆环周围的电场分布,而透射电磁波的右旋圆极化分量的幅度如图12(c)所示,可以看到携带2模式OAM波的右旋圆极化分量的幅度最大值明显地分布在两个圆环上,证明其携带的2模式OAM波不纯,有两个相位奇点.在 13 GHz这一频率该模型旋转 60°后转化效率下降明显.相位分布如图12(d)所示,绕该透射电磁波一周相位有4π的变化,但相位奇点非常明显地分成了两个,且相位分别不均匀,说明该分量的电磁波携带了不纯净的2模式的OAM.

图11 (a) 50°斜入射时的透射波;(b)介质圆环周围空间的电场分布;(c) 50°斜入射时 13 GHz 的右旋圆极化波的幅度;(d) 50°斜入射时在13 GHz的右旋圆极化波的相位Fig.11.(a) The transmission wave while incident angle is 50°;(b) E-field distribution around dielectric rings;(c) amplitude of RCP wave at 50° oblique incidence;(d) phase of RCP wave at 50° oblique incidence.

图12 (a) 60°斜入射时的透射波;(b) 60°入射时介质圆环周围的电场分布;(c) 60°斜入射时 13 GHz 的右旋圆极化波的幅度;(d)60°斜入射时13 GHz的右旋圆极化波的相位Fig.12.(a) The transmission wave while incident angle is 60°;(b) E-field distribution around dielectric rings at 60° oblique incidence;(c) amplitude of RCP wave at 60° oblique incidence;(d) phase of RCP wave at 60° oblique incidence.
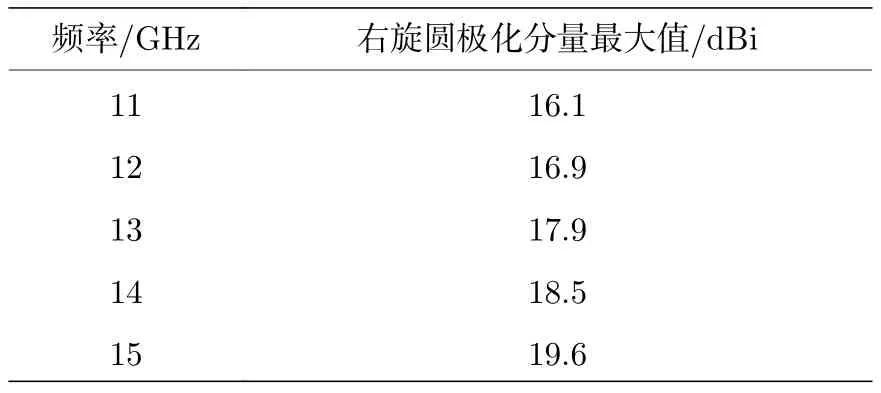
表5 60°斜入射时不同频点的左旋和右旋分量的最大值Table 5.Maximum values of RCP at different frequencies when incident angle is 60°.
表5列出了60°斜入射时不同频点的右旋分量的最大值.可见60°斜入射时,该模型可以转化入射的圆极化电磁波为交叉极化的OAM波,但转换效率相比垂直入射和小角度斜入射时低很多,会产生较多的反射分量.转化的中心频率更加明显地向高频移动,虽然其性能有所下降,但仍能明显观察到电磁波携带了轨道角动量.
4 结 论
本文利用场变换理论,提出了一种大角度涡旋电磁波产生方法.并基于场变换理论和简化参数近似方法设计了一种大角度涡旋电磁波产生媒质,构建出了产生2模式的OAM波的整体透射模型.该模型有着对入射角度不敏感的特性,在60°斜入射时仍能生成OAM波,实现了广角入射转化产生OAM波.此方法也可用于设计实现反射型和任意模态涡旋电磁波生成媒质.

