空心板桥静载试验横向分布效应计算探究

董林虓

（四川金通工程试验检测有限公司，四川 成都 610000）

我国交通行业一直保持高速发展，公路总里程数不断增加，既有桥梁数量也随之增加，桥梁检测的需求日益旺盛。在采用荷载试验的方法检验桥梁的承载能力时，计算方法的偏差可能造成对桥梁承载能力的错误判断。本文以实际工程为例，对比不同方法的计算结果与实际试验结果的偏差，旨在让理论计算结果更加贴近实际情况。

1 概述

1.1 工程概况

以一个实际工程为例，某简支空心板桥，桥梁上部采用1×16m标准跨径梁高80cm的C50预应力混凝土简支空心板梁，横向布置8片空心板，斜交角18°。支座采用板式橡胶支座，在两桥台处分别设置CD-40型钢伸缩缝。下部构造0号、1号桥台为重力式桥台，扩大基础。桥台两侧台尾各设置4.2m的桥头搭板。桥面铺装采用5cm混凝土铺装。

桥面布置：0.5m （护栏） +7.0m （行车道） +0.5m（护栏）；

桥梁荷载等级：公路-Ⅱ级。

1.2 试验方案布置

该桥计算跨径15.3m，理论基频5.62Hz，计算冲击系数0.289，总体荷载试验效率按进行控制，最终确定加载方案为采用2辆3轴车进行加载，2台车重量相同，均为35t，前轴重7t，中轴与后轴重均为14t。本文取中载工况为例进行分析。

2 横向分布计算

2.1 铰接板法计算

铰接板法需计算：1、单块板竖向抗弯惯矩I和抗扭惯矩IT。2、求板的抗弯刚度与抗扭刚度比例参数γ。3、根据γ从表中查出每一块板的横向分布影响线。4、进行布载，求出横向分布系数m［1]0。

按此方法进行计算：

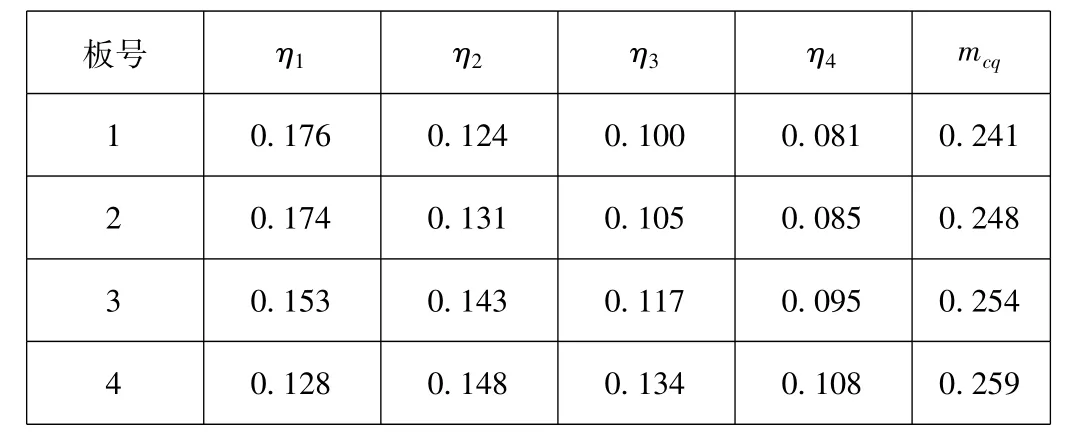
表1 铰接空心板桥荷载横向分布系数计算表

2.2 midas梁格模型计算

1）横向联系取顶板厚度，利用midas建立有限元梁格模型，采用斜交网格［2]，全桥共离散为451个节点，622个单元，截面外轮廓按矩形截面模拟，板间设置与空心板顶板等厚的横向联系梁，板间按铰接考虑，支座均按一般支座计算，经计算，得到各板跨中弯矩，1＃～4＃板依次为203.4 kN·m、266.2kN·m、275.9kN·m、329.2kN·m。

2）横向联系取全截面高度，建立midas模型，模型设置参数同2.2-1，板间设置与空心板等厚的横向联系梁，板间按铰接考虑，经计算，得到各板跨中弯矩，1＃～4＃板依次为243.8kN·m、253.2kN·m、261.3kN·m、268.5kN·m。

3 对比分析

将所有计算结果与实测结果进行对比，对比结果见表2。

表2 计算结果与实测结果差值表

经比较，横向联系取顶板厚度的midas模型计算结果最接近实际测试数据，空心板桥横向连接的模拟宜取铰接，连接高度宜取顶板厚度。有限元法较横向分布系数法计算结果更为精确，宜优先选用。