伽马射线暴X射线余辉中星风—星际介质转变的行为
秦松梅,李龙,王祥高*
(1.广西中医药大学 数理教研室, 广西 南宁 530001;2.广西大学 物理科学与工程技术学院, 广西 南宁 530004;3.广西大学—国家天文台天体物理和空间科学研究中心, 广西 南宁 530004;4.广西大学 广西相对论天体物理重点实验室, 广西 南宁 530004)
0 引言
伽马射线暴(gamma-ray burst, GRB)是宇宙中能量极高的爆发现象。它的持续时间在0.1~1 000 s,辐射主要集中在0.1~100 MeV的能段。当GRB爆发过后会在其它波段观测到辐射,称为GRB的余辉。根据波段不同可分为 X射线余辉、光学余辉、射电余辉等[1-2]。GRB余辉是研究其前先身、中心能源、辐射机制和暴周介质的重要窗口。多波段余辉的光变曲线和谱演化进行分析是对GRB的暴周介质的性质进行讨论的常见方法[3]。
GRB的持续时间一般以2 s为界,分为长暴和短暴两类。一般认为,几乎每一个长暴都与大质量恒星的死亡有关系[4-6]。而沃尔夫—拉叶星(wolf-rayet star,WR, 一种在正在演化的大质量恒星)被认为是长暴的前身星。WR星因其自身强劲的恒星风,导致恒星质量的高速流失,其恒星外层逐渐剥离。人们预期长暴的暴周环境会由星风介质向星际介质转变,形成一个星风泡状结构[7]。其粒子数密度分布将会从n(r)∝r-s(其中,n是粒子数密度,r是半径,s是指数)转变为n(r)∝r0。在这种情况下,星风环境终止在半径Rt~(1018~1020cm)处,密度以一个4倍以上的因子跳跃[8]。比如2003年DAI和WU[9]、2007年KAMBLE等[10]、2009年JIN等[11]、2010年KONG等[12]、2017年FRAJIA等[13]对这类工作进行了研究。
本工作将基于Swift/XRT大量余辉样本上,系统性搜寻星风介质向星际介质转变,并探讨其物理参量。本工作考虑一般的星风—星际介质转变的典型情形,即仅s=2向s=0的变化的情况。假设在星风—星际介质转变过程中喷流的磁能分配因子εB和电子能分配因子εe,以及激波加速后的电子能谱指数始终不变,且X射线波段的频率始终处于νm<νXRT<νc(其中νm是最小频率,νc是冷却频率,νXRT是Swift/XRT的观测频率)这一频率区间,在这种情况下,X射线余辉的光变曲线将会出现“由陡变平”,这一光变特征,本文对Swift卫星观测的X射线余辉进行系统搜寻,在其中寻找具有星风—星际介质转变现象的GRBs,以期研究物理特征。
1 数据处理
同步辐射产生的伽马暴余辉流量随时间和频率的变化为Fν∝ν-βt-α,其中α时间衰减指数。β为能谱指数。通过α和β的关系(closure relation)[14-17]可以很快判断观测结果是否满足余辉的标准模型,如表1。各种情形的closure relation可以参考文献[14,16-17]等。
对于余辉典型情况为处于慢冷却阶段和νm<νXRT<νc期间,对于s=2的星风介质:α=(3p-1)/4(p是同步辐射电子谱的谱指数),β=(p-1)/2;对于s=0星际介质:α=3(p-1)/4,β=(p-1)/2。可以看出如果电子谱指数p在星风—星际介质转变前后不变,在星际介质中的时间指数α将会比星风介质要小1/2,也就是说在长暴余辉的光变曲线中将会出现“由陡变平”的光变特征。

表1 星风介质以及星际介质环境下的余辉时间演化指数α和能谱指数β的关系
根据Swift官方网站提供的GRB观测数据,对从2004年12月到2018年12月Swift/XRT观测的GRB X射线余辉绘制其时间—流量关系图,其能段为0.3~10 keV。基于这些样本数据,对其进行时间分析得到其时间衰减指数α。时间分析采用分段幂律函数(如式(1))对数据进行拟合:
(1)
其中,α1和α2分别是转变前后的斜率指数,Tt是转变时间。同时,通过Swift官方网站提供的XRT能谱分析工具,获得余辉Tt时期的能谱指数据。
以GRB 080714为例,其光变曲线时变拟合结果为拐折前的衰减指数α1=1.58±0.06,拐折后的衰减指数α2=1.05±0.05,拐折后的时间衰减指数α2比拐折前的时间衰减指数α1小约1/2。而其拐折前能谱指数β1=0.62±0.48,拐折后能谱指数β2=0.65±0.31。其时间衰减指数α和能谱指数β满足符合closure relation。因此GRB 080714的X射线余辉符合星风—星际介质转变的观测特征。
2 结果分析
2.1 星风—星际介质转变的伽马暴候选体
通过对Swift卫星观测的1420个GRBs(截止至2018年12月1日)的X射线余辉进行详细的分析。采用分段幂律函数对数据进行经验拟合。结果得到了6个GRBs符合星风—星际介质转变的外激波模型,分别为GRB 080714、GRB 140509A、GRB 140614A、GRB 150309A、GRB 171020A、GRB 180425A。此外有4个GRBs(GRB 050721、GRB 080303、GRB 080714、GRB 100915A)虽然也能较好符合星风—星际介质转变的外激波模型,但其具有明显的谱演化行为,转变前后谱指数之差Δβ>0.2,因此未来纳入本工作的候选体范围。经验拟合结果如表2。表2中的α1和α2分别是转变前后的时间指数,β1和β2分别是转变前后的能谱指数。
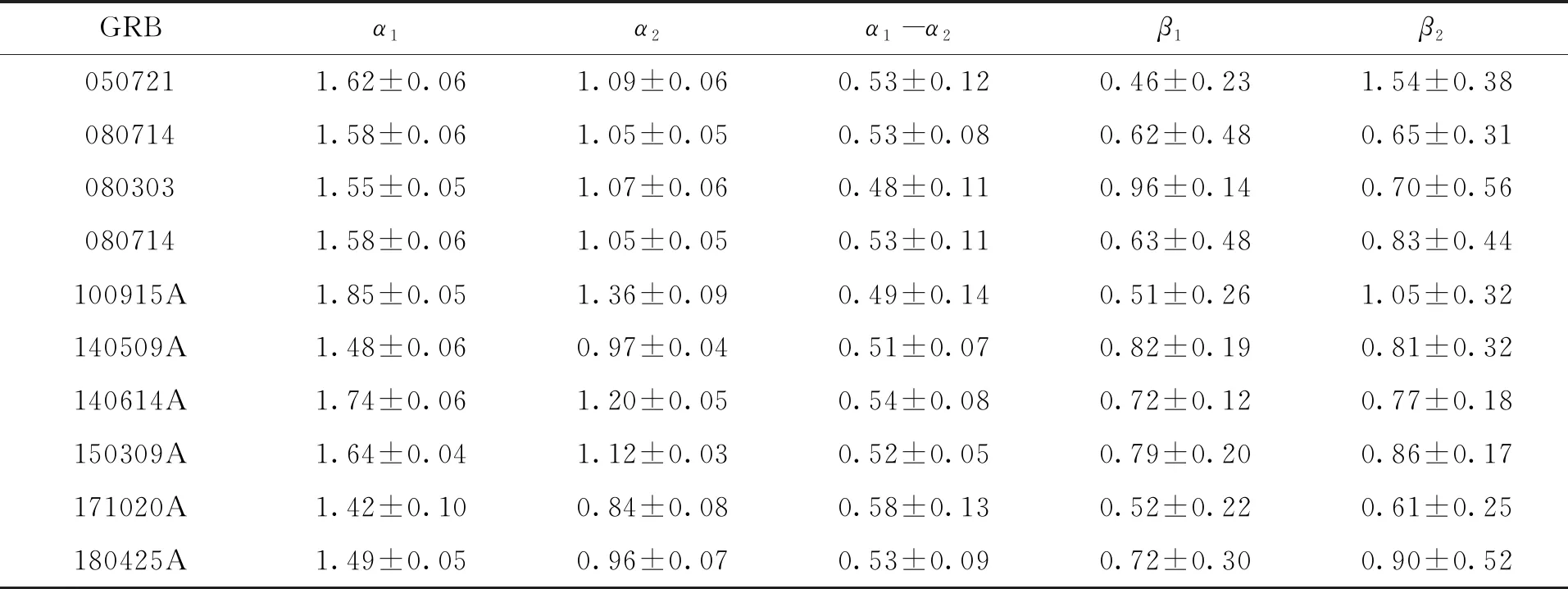
表2 拟合结果及相应的参数
2.2 物理参数的限制
考虑暴周环境由星风介质n(r)∝r-2向星际介质n(r)∝r0环境转变的标准外激波正向激波的模型,对Swift/XRT的数据进行拟合。我们模型的参数包括:磁场能量分配因子(εB),电子能量分配因子(εe),各向同性动能(EK,iso),初始洛伦兹因子(Γ0),星风介质密度参数(A*),星风—星际介质转变时间(Tt),密度跳跃因子(χ),喷流张角(θj),同步辐射电子谱谱指数(p)。
假设相对论激波穿过数密度为n的均匀冷物质,激波过后粒子数密度和能量密度分别是n2=4γn1,e2=4γ2n1mpc2。我们假定激波化的内能按一定比例(εe,εB)分给电子和磁场,因此得到电子的最小洛伦兹因子γm和磁场强度B:
(2)
B=(32πnmpεB)1/2γc。
(3)

(4)
电子系集体的同步辐射谱满足分段幂律函数形式:
(5)
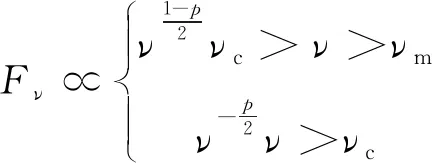
(6)
其中冷却频率νc和最小频率νm为幂律分布电子的同步辐射特征频率,对应于电子的冷却洛伦兹因子γc和最小洛伦兹因子γm。对于冷却频率νc,求解需要考虑到系统的动力学时标:当γe=γc时,同步辐射寿命等于系统动力学时标。则有:
(7)
瞬时谱不依赖于激波的流体动力学演化,但是,给定频率的光变则依赖于多个随时间而变的量:如拐折频率νm(t)和νc(t),峰值流量Fν,max(t)。这些又转而依赖于γ(t)和N(γe,t)如何随时间演化。
模型的动力学基于文献[19],动力学演化可以总结为如下形式:
(8)
dm=4πR2nmpdR,
(9)
(10)
其中,m是激波扫过的介质的质量,γ是激波的洛伦兹因子,Mej是伽马暴喷射物的质量,是激波的辐射效率。
星风介质密度参数由星风粒子数密度描述形式n(r)=Ar-2给出,其中:
(11)
(12)
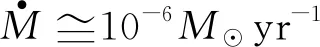
考虑星风向星际介质转变的外激波模型来对这6个GRBs进行拟合。基于目前有红移的461个长暴进行统计,得长暴红移符合高斯分布,其典型值z~(1.5±1.1)(图1)。对于红移未知的GRBs,取红移典型值z=1.5。样本中均不存在明显的onset bump行为,因此模型无法对Γ0以严格的限制,Γ0取典型值200;磁能分配因子εB取经验值10-5[16,21-25];星风密度参数A*取典型值1。图2为基于考虑星风—星际介质的外激波模型的拟合图。表3为其详细物理参数。

图1 长暴红移分布直方图
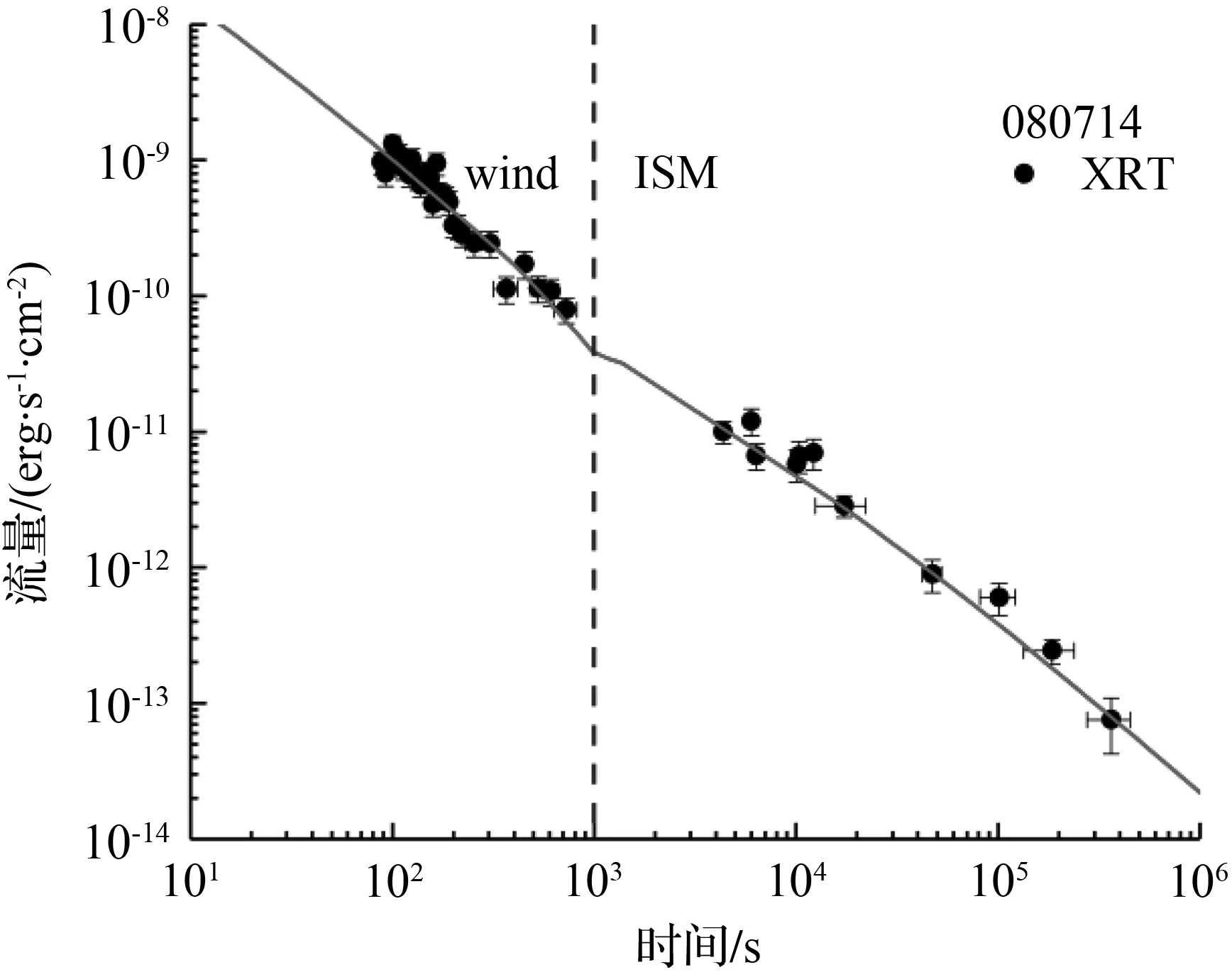
(a) GRB 080714光变拟合图

(b) GRB 140509A光变拟合图

(c) GRB 140614A光变拟合图

(d) GRB 150309A光变拟合图
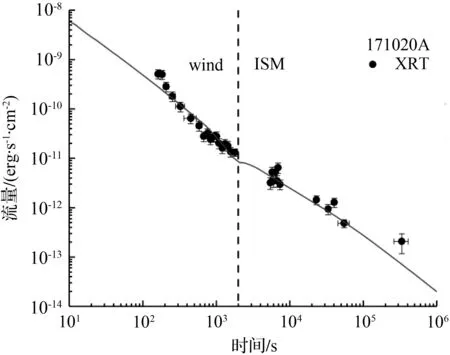
(e) GRB 171020A光变拟合图

(f) GRB 180425A光变拟合图
图2 光变曲线拟合图
Fig.2 Fitting result of the light-curves
具有星风—星际介质转变GRBs的EK,iso在1053到1054erg之间,与一般长暴的典型值相比要小一些[16]。p在2.1~2.6,与不是星风—星际介质的GRBs能量及其电子谱指数据分布一致。密度跳跃参数χ在4~10,与CASTOR和WEAVER等的研究结果一致[7,26]。Rt在1016~1017cm,比典型值Rt~(1018~1020cm)小[8]。这可能是因为星际介质密度很高(伽玛暴前身星处在致密的分子云区域),导致星风区域被限制在很小的尺度。

表3 星风—星际介质转变GRBs的一些物理参数
3 结论
通过大样本GRB X射线数据拟合分析,用考虑考虑了星风—星际介质转变的外激波模型时时间指数α和能谱指数β的关系(closure relation)对数据进行限制,得到6个GRBs(GRB 080714、GRB 140509A、GRB 140614A、GRB 150309A、GRB 171020A、GRB 180425A)具有星风—星际介质转变的特征。我们发现:
① 具有星风—星际介质转变的GRBsEK,iso在1053~1054erg,与一般长暴的典型值相比要小一些。
②p在2.1~2.6,与不是星风—星际介质的GRBs能量及其电子谱指数据分布一致。
③ 具有星风—星际介质转变的GRBs在喷流张角比较大,大部份大于10度。
④ 星风—星际介质转变时间一般在暴后800~2 000 s,转变半径Rt在1016~1017cm。
这些参数将为我们研究进一步研究伽马暴物理提供更多线索。如此少数量的GRBs具有星风—星际转变的特征,可能原因之一是本工作只采用了s=2的星风介质下的模型对数据进行限制,而星风介质的s值可能会小于2或者大于2。另外一个原因是GRB X射线的频率可能会处于νm<νc<νXRT, 或者νm<νc<νXRT和νm<νXRT<νc两种情形都有,在这种情况下,星风—星际介质转变的光变曲线将会变的十分复杂。而现在的模型只考虑νm<νXRT<νc辐射区。

