需求及建设成本不确定下考虑失效的内陆港选址研究
范厚明,郭健,宋冠男,蒋晓丹
(大连海事大学 交通运输工程学院, 辽宁 大连 116026)
0 引言
内陆港的合理选址可有效增强腹地货流的吸引力、提升多式联运网络运营效率。在选址决策中,货运需求和内陆港建设成本是要考虑的关键因素,二者均具有不确定性。同时,受自然灾害、人为灾害等因素的影响,内陆港存在失效风险,失效一旦发生将导致选址网络发生改变,严重影响内陆港系统的响应能力。因此,需求和建设成本不确定及节点失效下的内陆港选址问题已引起学者们广泛关注。
有关需求或建设成本不确定下内陆港选址问题研究,WEI等[1]利用网络层次法解决了内陆港选址中需求不确定性问题;范厚明等[2]以概率情景和鲁棒性对需求进行描述,构建了需求不确定和路径可靠性的内陆港选址模型,设计粒子群—模拟退火算法进行求解;王国利等[3]以概率情景描述需求的不确定性,构建了基于需求及供应不确定的设施选址模型,并应用拉格朗日松弛算法对模型进行求解;ZETINA等[4]以不确定区间来描述需求和运输成本的不确定性,构建了综合考虑不确定需求和运输成本的枢纽选址模型,并设计割平面法进行求解;林殿盛等[5]以随机约束描述需求的不确定,并基于此构建考虑需求不确定和碳排放的选址模型,利用LINGO对模型进行求解,结果表明需求的变动对选址结果会产生较大影响;万波等[6]以概率情景和P-鲁棒优化对需求不确定进行描述,构建需求不确定下的层级设施选址模型,应用遗传算法对模型进行求解;孙清臣等[7]以概率情景描述三类应急物资需求的不确定性,构建随机模型并设计样本均值逼近算法求解;MOHAMMADI等[8]以区间随机数表示节点间货运需求的不确定性,构建综合考虑环境成本函数的枢纽选址模型,并设计模拟退火算法求解;MESTRE等[9]以不同情景集刻画不确定需求,建立了两个医院网络的选址模型并求解;MERAKL等[10]以软管模型描述节点需求的不确定性,构建需求不确定下带容量约束的选址模型,并设计Bender分解算法求解。
ALUMUR等[11]以情景集来描述航空节点需求和建设成本的不确定性,构建无容量约束下的选址模型,并用CPLEX对模型进行求解;BOUKANI等[12]以不同情景集来描述枢纽建设成本和容量的不确定性,构建了建设成本和节点容量不确定下的鲁棒优化模型,并应用GAMS求解。
有关节点失效对选址的影响研究,PANT等[13]建立了多区域故障输入—输出模型对内陆港失效进行研究,认为考虑失效可以提高内陆港选址的合理性;BORZOU等[14]建立了考虑节点失效下的单分配枢纽选址问题,设计了Benders分解算法求解;于东梅等[15]构建了需求不确定及设施失效下的鲁棒优化模型,并设计蝙蝠算法求解;周娜等[16]构建了考虑节点失效及客户重分配的选址模型,并设计拉格朗日算法求解;王帮俊等[17]建立了考虑枢纽失效和拥堵情形的选址模型,并设计改进粒子群算法求解;MOHAMMADI等[18]构建了考虑节点失效下的多目标选址模型,设计了基于博弈的元启发式算法求解。
梳理发现,当前内陆港选址领域中还未有综合考虑需求、建设成本不确定及节点失效的研究成果,但在实际中需求和建设成本的不确定性及节点失效均对选址结果有重要影响,综合考虑三者对内陆港的合理选址及提高联运网络的鲁棒性具有重要的现实意义。综上,笔者考虑了需求和建设成本两个不确定因素以及节点失效对内陆港选址的影响,以内陆港的建设成本、运输成本、中转成本和内陆港失效后的惩罚成本在内的总成本最小为目标,构建综合考虑需求和建设成本不确定,以及节点失效的鲁棒—随机选址模型,并设计粒子群—模拟退火算法求解,最后通过算例分析验证模型的有效性。
1 模型构建
1.1 问题分析与前提假设
1.1.1 问题分析
内陆港选址问题是战略决策问题,决策结果会产生长期影响,因此在选址决策期间合理地考虑内陆港建设及运营期间存在的不确定因素来提高选址结果的鲁棒性十分重要。
本文考虑三方面不确定因素:①内陆港建设成本是影响选址结果的重要因素,而在土地价格、内部设施成本、人工费及材料费等因素的影响下,内陆港的建设成本存在不确定性;②季节、客户需求等的变化均会影响货主点的货运需求,且新的内陆港的建立可能会刺激新的运输需求,因此货主点运输需求也具有不确定性;③在自然灾害等因素的影响下内陆港存在失效风险。
从以上分析可看出需求和建设成本的不确定性及节点失效在内陆港建设及运营期间均可能发生且会对选址网络产生影响,因此在内陆港选址决策期间充分考虑需求和建设成本的不确定性及节点失效是科学且合理的。
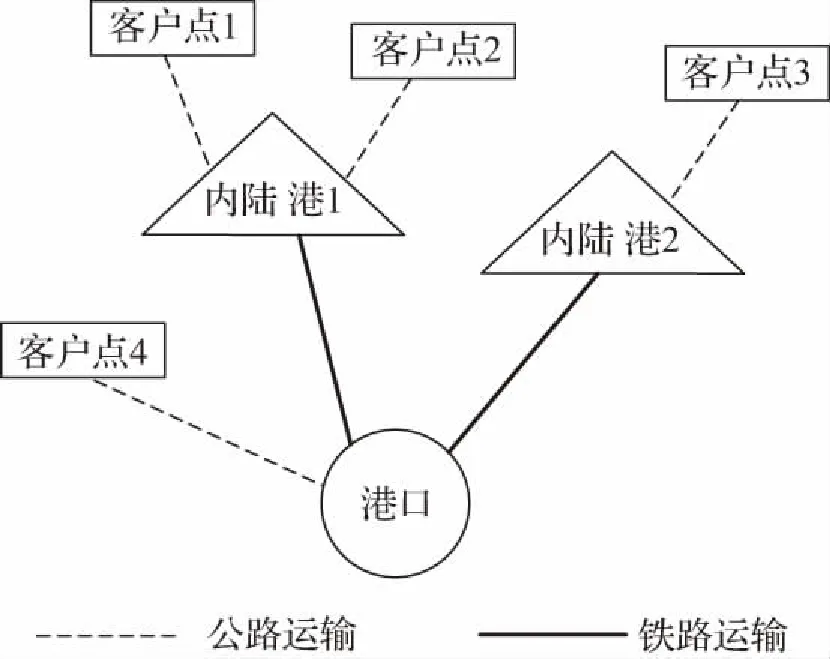
图1 内陆港网络拓扑图
本文研究的问题为:由I个需求点、K个内陆港节点和一个港口组成的内陆港多式联运网络,其中需求点货流可通过公路运输至内陆港后经铁路转运至港口,也可以经过公路直达港口。内陆港网络拓扑图如图1。
决策者在港口腹地筛选出若干城市作为内陆港候选点,并在考虑需求和建设成本不确定及节点失效下进行选址研究,结果可为内陆港的建设数量和布局等决策提供科学依据。
1.1.2 前提建设
本文构建的内陆港选址模型假设如下:
① 各个货主的货物只能选择一条路径运输至海港;
② 内陆港所在城市的运输需求只能通过当地内陆港转运;
③ 各个内陆港处的最大容量恒定;
④ 不考虑内陆港失效后仍能继续提供服务的情况。
1.2 符号说明
本文定义的相关符号如下:

1.3 需求及建设成本不确定下考虑失效的内陆港鲁棒—随机选址模型构建
本文构建的需求及建设成本不确定下考虑节点失效的内陆港鲁棒—随机选址模型如下:
目标函数:
(1)
(2)
约束条件:
(3)
(4)
qhzh≥R,∀h∈H,
(5)
(6)
(7)
Yih0(tih+tlr+th0)+Yi0ti0≤ti,∀i∈I,
(8)
Yih0≤zh,
(9)
(10)
(11)
zh∈{0,1},
(12)
Yih0,Yi0∈{0,1}。
(13)
模型中,式(1)表示最小化各选址方案在各建设成本情景下的最大后悔值,后悔值为选址方案在建设成本情景下的目标函数值与该情景下最优目标函数值之差;式(2)表示在特定建设成本情景S下最小化各需求情景下总成本期望值,总成本为内陆港建设成本、货物运输成本、中转成本以及考虑内陆港失效下的惩罚成本总和。
式(3)表示货流只能选择一条路径运输;式(4)表示确保每个需求点所有货物均能运出;式(5)表示系统的可靠性约束,即选定的任一内陆港h的可靠性均大于某一定值;式(6)表示内陆港选择数量;式(7)表示运输至内陆港h的货物量不能超过内陆港h的最大容量约束;式(8)表示各个货主的货物运输时间约束;式(9)表示各个货主所转运的内陆港必须是已选定的内陆港;式(10)、(11)表示非负约束;约束(12)、(13)表示内陆港的0-1约束。
2 粒子群—模拟退火算法
2.1 算法选择
本文研究的问题为NP难问题,网络的复杂度取决于节点、内陆港、建设成本和需求情景集的数量,对于大规模问题,精确算法求解时间长,可以采用启发式算法得到满意解。粒子群算法具有参数少、简单易实现的特点,但算法进化后期搜索精度不高、收敛速度变慢,容易陷入局部最优;而模拟退火具有概率接受劣解机制,可以突破局优,且上述两种算法的结合在文献[2,19]中均得到了很好的应用。基于此,本文设计粒子群—模拟退火算法对模型进行求解。
粒子群—模拟退火算法包括三种策略:
① 参数调整策略
惯性权重和加速因子影响着粒子群的全局与局部搜索能力、收敛速度与精度,因此,本文对参数进行调整[20]。具体如下:
惯性权重:
(14)
(15)
其中,ωmax和ωmin分别为惯性权重最大最小值;Tmax为最大迭代次数;φ为幅度;m为周期参数;α(t)为自适应因子,其中f(pg)与avg(f(pi))分别是第t次迭代中全局最优值和所有粒子的平均适应度值。
加速因子:
(16)
(17)
式中,c1max,c1min,c2max,c2min分别是两个加速因子的最大最小值。
② 概率接受劣解策略
在粒子的迭代中,若新一代粒子的适应度值劣于其个体最优适应度值,则采用模拟退火的概率接受劣解的策略来处理。如果满足概率机制,则对个体最优进行更新。
③ 局部搜索策略
在粒子群算法中,个体极值与群体极值的质量影响着种群的进化。因此本文对个体极值进行局部搜索以增强个体极值和全局极值的质量,提高算法的效率。
2.2 粒子群—模拟退火算法流程
粒子群—模拟退火算法流程如图2。
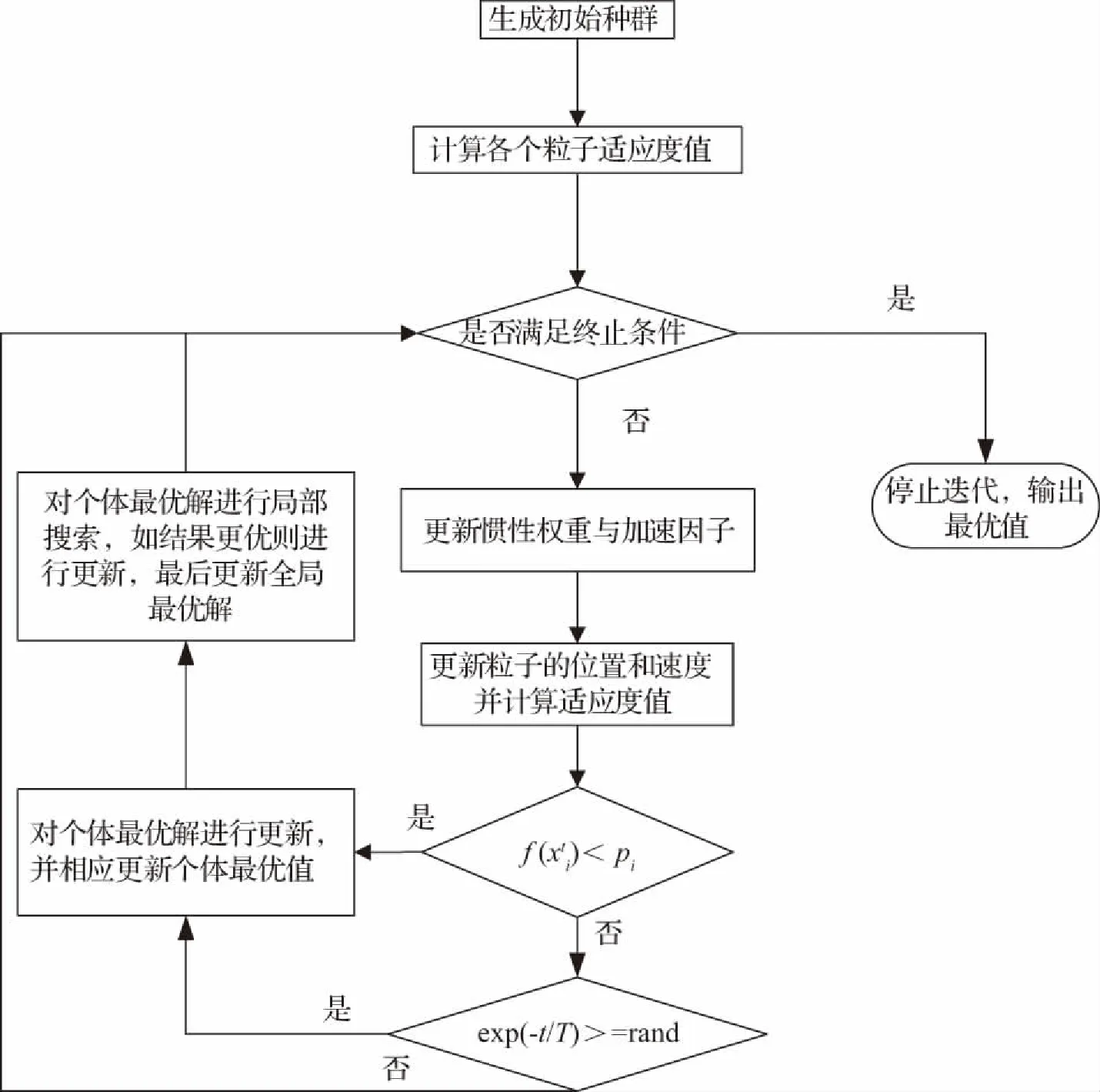
图2 粒子群—模拟退火算法流程
粒子群—模拟退火算法步骤如下:
Step1:设粒子数为N,初始化粒子的位置和速度,设置惯性权重相关参数ωmax,ωmin,φ,m;设置加速因子相关参数c1max,c1min,c2max,c2min。初始迭代次数t=1,最大迭代次数为T。由此形成初始粒子群p0。设每个粒子的当前最优解pi为其当前位置,计算各个粒子的适应度值,其中适应度值最高的粒子为全局最优解pg。
Step2:利用式(14)~(17)更新粒子的惯性权重和加速因子。

(18)
(19)
Step4:计算新一代粒子适应度值并与其个体最优值进行比较,若结果更优则对个体最优进行更新;若结果更差则进行判断,若exp(-t/T)≥rand,则更新个体最优(对于前一代全局最优粒子不进行该项判断)。
Step5:对于更新后的粒子群的个体最优粒子进行局部搜索,若结果更优则对个体最优进行更新,最后更新全局最优。
Step6:判断是否满足结束条件,满足则停止迭代,输出最优解,否则返回step2。
3 算例分析
3.1 算例描述
本研究采用算例对模型进行检验,在平面(1 000 km×1 000 km)内随机产生节点作为研究对象。其中节点1~35为经济发达、交通便利,方便货物的集散,因此将这些点作为内陆港的候选点,节点36~40因地理位置、经济等方面存在不足,作为纯货运需求点,编号0为港口。
根据现有文章中参数的设置,本文设计了一组参数进行算例研究。模型中,取折扣因子λ=0.8,内陆港个数K=5;权重ω=0.8;单位惩罚成本c=1 500;内陆港系统可靠性系数R=0.6;每个内陆港的可靠性qh∈(0,1)[2-3]。算法中取加速因子c1max=2.75,c1min=1.25;加速因子c2max=2.25,c2min=0.5;m=4;惯性权重ωmax=0.9,ωmin=0.4;权值φ=0.1;最大迭代次数T=600[20]。
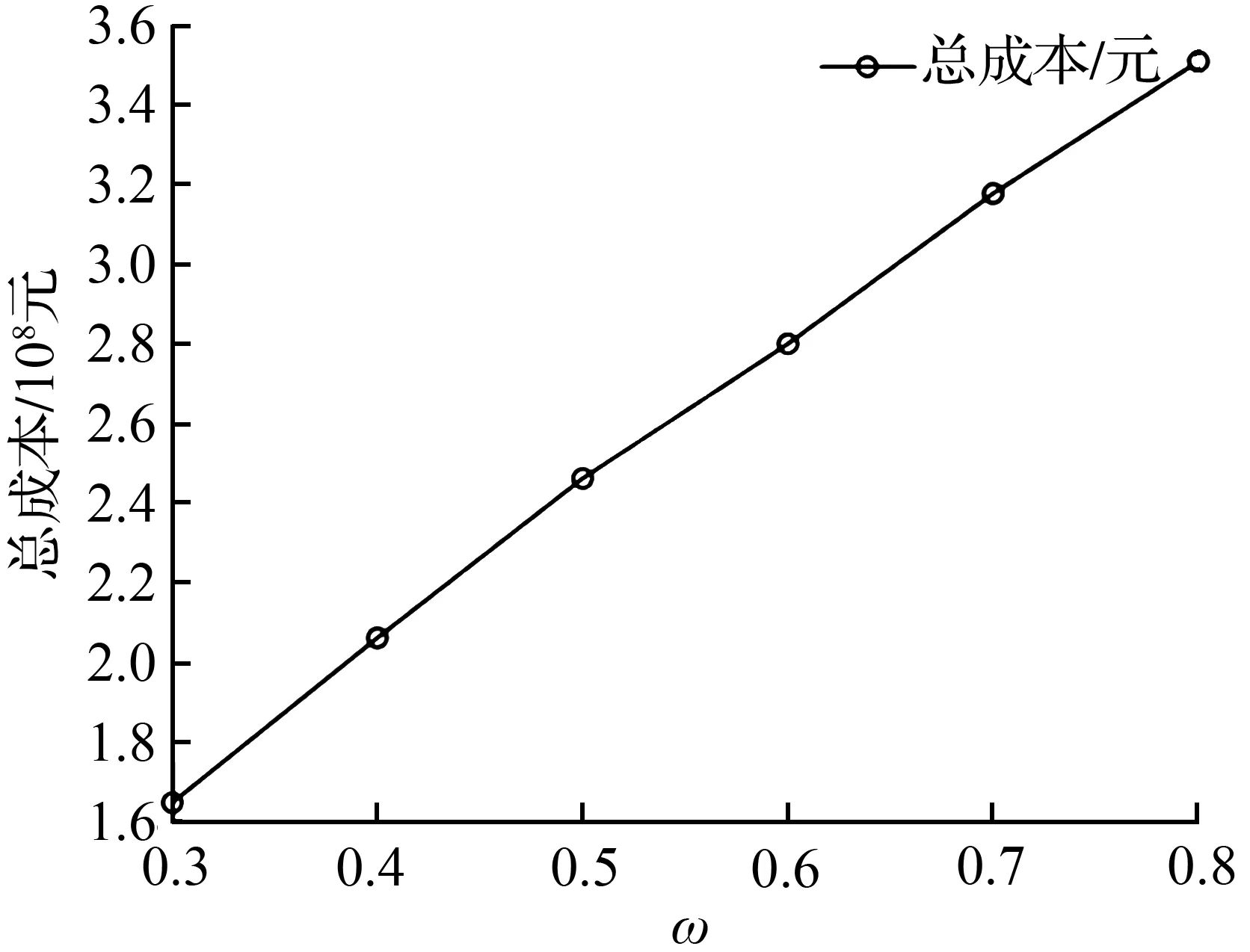
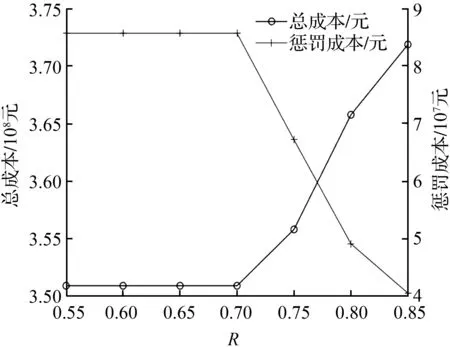
模型中涉及货主点运输时间限制,本文中货主最大运输时间参考文献[21]适当取值,具体如下:当0 根据交通运输部制定的公路和铁路的运输速度和运价,以及现存内陆港的具体数据对公路和铁路的运输速度、运输成本、转运成本和时间取值,如表1。其中公路转铁路的中转成本取为120元/TEU,中转时间取为5 h。 表1 公路/铁路相关数据 本文内陆港建设成本与容量结合内陆港选址实际与文献[22]取适当值。其中,关于内陆港建设成本情景集的设计,首先生成一组基准建设成本情景s1,在此基础上,根据我国建设项目的可行性研究阶段对投资估算允许产生误差的规定,本文在基准成本的±20 %以内再随机产生三组建设成本。具体数值如表2。 表2 各个情景下节点的建设成本及容量 本文采用的是平均建设成本,即上述总建设成本与折旧年限之比,根据企业所得税法对固定资产折旧年限的最新规定,折旧年限T取20 a。 表3 各情景下的货主需求 在鲁棒—随机选址模型中,首先应求得各个建设成本情景下随机模型的最优值,然后将所求的最优值代入到后悔值模型中,计算综合考虑4组建设成本情景下的鲁棒选址方案。并在此计算结果基础上,根据式(1)计算所求的鲁棒—随机解在各个建设成本情景下的后悔值,并计算其与相应的最优值之比,即偏差比,计算结果见表4。 表4 模型求解结果 由表4可见,鲁棒—随机选址模型求得的选址方案在各个情景下的后悔值占最优值之比均小于1.5 %,说明求得的选址结果当任一情景发生时都是较优的,选址结果具有很好的鲁棒性。 上述求解结果表明,决策者在内陆港选址规划阶段应对需求和建设成本作合理预测,并考虑其可能的变化范围,以便得到更贴合实际的鲁棒选址方案。同时从表4中可见,在所求的4组建设成本情景下的随机最优解中,节点11均有出现,说明节点11对不确定需求及建设成本均具有很强的鲁棒性。这一方面说明该点的运输需求量较大,另一方面也说明该点具有很好的地理优势。因此,决策者在进行大规模的内陆港选址时,可以先根据各城市的货运需求及地理位置选出枢纽内陆港适建点,再在此基础上寻找其他内陆港点以提高内陆港系统的稳定性,节约选址成本。 在以上结果下,最优选址结果及路径拓扑图如图3。 图3 最优路径拓扑图 在该组选址结果及路径分配下,内陆港2承担了51 894 TEU货物的运输,占比约21 %;内陆港10承担了22 710 TEU货物的运输,占比约9 %;内陆港11承担了57 138 TEU货物的运输,占比约为23 %;内陆港13承担了36 417 TEU货物的运输,占比约为15 %;内陆港25承担了55 160 TEU货物的运输,占比约为22 %。5个内陆港共承担了约90 %TEU的货物,提高了内陆港货运网络的效率。 3.3.1 内陆港失效分析 为对考虑内陆港失效下模型的有效性进行分析,本文在建设成本情景s1、需求情景s1′下,考虑内陆港失效的影响,则选址模型为: 目标函数: (20) 约束条件: s.t(3)~(13)。 在同样情境下,当不考虑内陆港失效时,选址模型如下: 目标函数: (21) 约束条件: s.t(3)~(13)。 对以上两个模型求解并列出各项成本作对比分析,结果如表5,其中在求解出不考虑失效的选址模型最优解基础上,代入相关失效参数求出该最优解下的惩罚成本,即不考虑失效的选址模型的惩罚成本。从表5中可以看出,相比不考虑内陆港失效的选址模型,考虑失效后的选址模型尽管建设成本、运输及中转成本综合有一定程度的增加,增加约50万元,但是内陆港失效带来的惩罚成本却有大幅度的减少,减少了约2 200万元。由此可见建设成本和运输成本的少量增加便能有效地降低内陆港失效的惩罚成本。因此决策者在进行内陆港选址时,考虑内陆港失效可有效提高内陆港运营的稳定性,避免内陆港失效带来的风险。 表5 求解结果对比 当决策者对基础成本(建设成本、运输及中转成本)和内陆港失效导致的惩罚成本的偏重不同时,也会产生不同的结果。在建设成本情景s1、需求情景s1′下对考虑失效的选址模型进行求解,计算不同ω下各类成本的变化,结果如图4和图5所示。 图4ω不同时总成本的变化 Fig.4 Changes of total cost with differentω 图5ω不同时基础成本和惩罚成本的变化 Fig.5 Changes of base costs and penalty costs with differentω 从图4和图5中可以看出,当ω增大时,总成本和惩罚成本增大,基础成本减少。因此,在选址决策中,若决策者偏向于降低基础成本,则应适当选择较大的ω;若决策者偏向于降低失效风险带来的惩罚成本,则应适当选择较小的ω。 3.3.2 系统可靠性分析 在建设成本情景s1、需求情景s1′下对考虑失效的选址模型进行求解,计算R不同时的总成本及惩罚成本,结果如图6。 从图6中可以看出,当可靠性R的值高于0.7时,选址结果倾向于更加可靠的一组节点,这使得内陆港失效风险成本大幅减少,总成本略有增加;当R的值高于0.85时,将找不到可行解。由此可见,决策者在进行内陆港选址决策中,应充分对候选内陆港节点进行调查,以确定各个候选内陆港节点的失效概率,并对内陆港系统要达到的可靠性进行合理的判断以得出更满意的选址结果,避免投资浪费。 3.3.3 容量分析 内陆港容量影响货流对路径的选择,进而影响网络总成本。本文在建设成本情景s1、需求情景s1′下对考虑失效的选址模型进行求解,计算容量不同时的总成本及内陆港覆盖货流量,计算结果如图7。 图6R不同时的成本变化 Fig.6 Change of cost with differentR 图7 内陆港容量的变化对总成本及覆盖货流量的影响 Fig.7 Impact of changes of inland port capacity on total cost and coverage 从图7中可以看出,随着内陆港容量的减少,内陆港网络覆盖的货流量随之减少,更多的货流选择公路直达港口,这导致了内陆港总成本增大;而随着内陆港容量的增加,虽然网络覆盖的货流量保持不变,但货流可更灵活地选择更近的内陆港进行转运,这带来内陆港总成本的减少。当容量增加量超过20 %时,总成本将保持不变。由此可见内陆港的容量对总成本有极大影响,容量过高将导致内陆港冗余,过低将造成需求流失,引起总成本的增大。因此决策者在进行选址的同时应充分考虑内陆港的容量以制定更为合理的方案。 本文针对考虑需求和建设成本不确定及节点失效下的内陆港选址问题进行的研究主要结论如下: ① 鲁棒—随机选址模型求得的最优解可有效降低各情景发生时的最大后悔值,能较好地解决内陆港选址中需求和建设成本不确定问题,减少投资风险。 ② 考虑内陆港失效可以明显降低失效风险带来的惩罚成本,并能有效提高内陆港系统的可靠性。 ③ 内陆港容量的变化对总成本有很大影响,合理的容量可在覆盖更多货流的情况下使总成本达到最优,避免内陆港的冗余。本文研究成果丰富了内陆港选址领域中对不确定性问题的理论研究,可为经营者实际内陆港选址的相关决策提供科学依据。

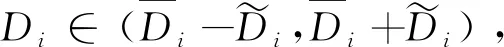

3.2 鲁棒—随机选址模型求解


3.3 结果分析



4 结论

