环Z4上自对偶码的一种构造
王艳萍
(宿州学院 数学与统计学院,安徽 宿州 234000)
0 引 言

1 环Z4和 环Z4+vZ4上的线性码
首先给出Z4上的线性码.

x·y=x0y0+x1y1+…+xn-1yn-1;


注1如果自对偶码C的dE(C)达到上述引理中的上限,称它为Z4上的极优码.
下面给出环Z4+vZ4(v2=v)上的线性码.
如下文特殊说明,我们可记R=Z4+vZ4(v2=v).对∀r∈R,有r=a+vb,a,b∈Z4,且这样的表示唯一.我们把环上的单位记作U,U={1,3,1+2v,3+2v};而环上的理想为:{0},Z4+vZ4,<2v>={0,2v},<2+2v>={0,2+2v},
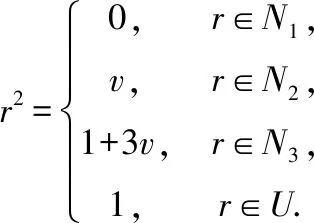
环上r=a+vb的重量wE:wE(a+bv)=wE(a+3b)+wE(3a+2b).


2 R上的自对偶码及Gray像
对∀c=(c0,c1,…,cn-1)∈C,我们可分别记nU(c):c中分量属于U的个数;记nN1(c):c中分量属于N1的个数;记nN2(c):c中分量属于N2的个数;记nN3(c):c中分量属于N3的个数.
注2当C⊆C⊥,称C是R上的自正交码;当C=C⊥,称C是R上的自对偶码.
定理2C是R上的线性码,则:
(1)如果C⊆C⊥,即C是正交码,则∀c∈C,有nU(c)+nN3(c)≡0(mod4),nN2(c)+3nN3(c)≡0(mod4);且有wE(c)≡0mod(4).
(2)如果C=C⊥,即C是自对偶码,则C包含向量(2+2v,2+2v,…,2+2v).

(2)因对∀r∈R,当r∈U,N3时,有r·(2+2v)=2+2v;当r∈N1,N2时,
r·(2+2v)=0;设C=C⊥,∀c∈C,(2+2v,2+2v,…,2+2v)·c=[nU(c)+nN3(c)]·(2+2v),由(1):nU(c)+nN3(c)≡0mod(4),所以(2+2v,2+2v,…,2+2v)·c∈C⊥=C,即证结论.
接下来我们讨论R上自对偶码的Gray像的性质.
定理3C是R上的线性码,其长n,则有φ(C⊥)=φ(C)⊥.

注3由上述定理知:φ是保正交的.也就是说对∀c1,c2∈Rn,且c1c2=0,则有φ(c1)φ(c2)=0;
注4由上述定理4,易知,若C是类型Ⅰ(Ⅱ)码,且长度为n,则φ(C)亦是类型Ⅰ(Ⅱ)码,且长度为2n.
注5显然可知2v∈R,<2v>是自对偶码,长是1,且为类型Ⅰ码,由文[12]可知,R上类型Ⅰ码(任意长度)均存在.
引理2[7]对Z4上长为n的自对偶码C,n≡0(mod8)⟺∃C是类型Ⅱ码.
定理4对R上类型Ⅱ码存在,且长度为n⟺n≡0(mod4).
证明 “⟹”因φ:保距,由上述引理2知,如果R上类型Ⅱ码存在,且长度为n,则n≡0(mod4);
“⟸”若令C=<(2,0,2,0),(0,2,0,2),(2,0,0,2),(0,2,2,0)>,显然其长度为4,且我们易知,每个码字的重量均是8,由文[12]知C×C,C×C×C,…依次是长8,12,16,……的类型Ⅱ码.即证.



3 实 例
通过上述所研究结论,可构造出Z4上的一些码.
例1 当n=1时,若取C1=<2v>,则C1是环R的自对偶码,参数是(1,4,4)且为类型Ⅰ最优码;而φ(C1)是长度为2,重量为4的参数为(2,4,4)类型Ⅰ码.
例2 当n=2时,若取C2=<(0,2),(2,0)>,则C2是环R的自对偶码,参数是(2,16,8)且为类型Ⅱ极优码;而φ(C2)是长度为4,重量为8的参数为(8,16,8)类型Ⅱ极优码.
例3 当n=3时,若取C3=<(2,0,0),(0,2,0),(0,0,2)>,则C3是环R的自对偶码,参数是(3,64,8)且为类型Ⅱ极优码;而φ(C3)是长度为6,重量为8的参数为(12,64,8)类型Ⅱ极优码.

