基于支持向量机的细颗粒物日均浓度预测
杨婳妍,吴育联,朱婧巍,易凡茹,吴小涛
( 黄冈师范学院 数学与统计学院,湖北 黄冈 438000)
细颗粒物(Fine Particulate Matter, PM2.5)是指直径不大于2.5微米的颗粒物,具有直径小、活动能力和吸附有毒物质能力强、总面积大的特征,随着空气流动四处扩散,对人类健康构成威胁[1]。通过对PM2.5日均浓度的预测研究,人们可以及时地获得某个区域的PM2.5浓度,在一定程度上避免去浓度超标的区域活动,保护身体健康,或者提前做好防护工作,消除空气质量的不良影响;政府相关部门也可以进行合理的安排规划,根据具体情况做出正确的决策,为社会公众更好地服务[2];环保部门更加准确的掌握PM2.5浓度的变化规律,预测结果可以为环保部门治理PM2.5时提供分析依据。综上所述,预测PM2.5日均浓度具有十分重要的现实意义。
近年来,国内外学者对PM2.5浓度预测进行了大量的研究。如冯樷、姚达文等[3-4]采用神经网络模型对PM2.5进行了预测,并与多元统计预测模型比较,发现神经网络模型的预测精度更高,但是模型结构的参数需要经过多次调整,准确率才能有效提高,因此其计算复杂度较大。Zhou等[5]利用集合经验模态分解(EEMD)和广义回归神经网络(GRNN)混合模型对PM2.5浓度进行了预测,虽然预测精度较神经网络模型高,但是在对原始序列进行EEMD后得到的子序列较多,分别建立预测模型使得计算复杂度较大。谢申汝等[6]利用LIBSVM模型对PM2.5浓度进行预测,最大的特点是由于SVM模型只含有两个参数,调整起来很方便,但是并没有给出这两个参数的优化算法。
本文提出了一种基于集合经验模态分解(EEMD)和样本熵(SE)、粒子群优化最小二乘支持向量机(PSO-LSSVM)的PM2.5组合预测模型,来对PM2.5日均浓度进行短期预测。通过EEMD,原始序列被分解为多个分量序列,可降低原始数据的复杂度和不稳定性;样本熵对EEMD得到的分量进行重组可以简化计算,提高运算效率;对重组后的新分量分建立LSSVM预测模型进行预测,PSO算法对LSSVM预测模型的参数优化,提高模型的预测精度;最后将各个LSSVM预测模型的预测结果叠加得到最终的预测值。
1 理论和方法
1.1 集合经验模态分解
EEMD算法[7]是在经验模态分解(EMD)算法上改进得到的,EMD的基本思想是对于某个非平稳的序列,分析序列的局部特征尺度(极值点),把尺度不相等的波动逐步地筛选,从而得到若干个不同的分量。由于EMD属于递归模式分解算法,包络线估计误差在分解过程中不断累积,所以存在模态混叠现象。EEMD则是通过加上一些高斯分布的白噪声在原始信号序列上,解决原始EMD模式中存在的混叠问题。EEMD的具体分解步骤如下:
步骤1:将若干个随机高斯白噪声序列ωm(t)加入到原始信号序列x(t)中,组成信噪混合序列:
Xm(t)=x(t)+ωm(t)
(1)
步骤2:对Xm(t)进行EMD分解,得到n个IMF分量ci,m(t),i=1,2,…,n,以及一个剩余分量ωn,m(t),即
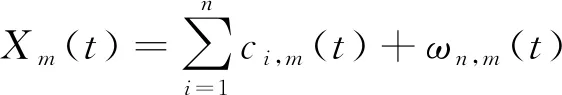
(2)
步骤3:将不同的高斯白噪声序列加到原始信号序列x(t)上,重复之前的两个步骤,得到IMF分量和剩余分量,一共记录下M组不同的数据;
步骤4:对上述M组IMF分量及剩余分量组合,分别计算均值,作为EEMD的分解结果,表示为:

(3)

(4)
序列采用EEMD分解得到的分量个数往往随着序列规模的增加而增加,为了降低预测的时间复杂度,本文基于样本熵理论,对EEMD分解得到的分量进行重组。
1.2 样本熵
样本熵(SampEn)是由Richman等于2000 年基于近似熵(ApEn)提出的一种时间序列复杂性测度方法。序列的复杂度越低,样本熵值就越小;反之,样本熵值就越大[7]。对于EEMD 得到的分量,如果直接对每个分量分别建立预测模型进行预测,不仅会增加计算的规模,而且还忽略了分量之间的相关性,因此将具有相关性的分量序列利用样本熵进行重组,这样不仅能够减少运算时间,还能突显同类分量序列的特性。
样本熵可用SampEn(Num,m,r)来表示,其中Num表示序列的长度,m表示序列的维数,r表示序列的相似容限。给定序列样本熵的计算步骤如下:
步骤1:将Num个数据点的时间序列依照数据点的排序,以m个数据点为一个子片段进行划分,总共可以得到Num-m+1个子序列片段,记为X(i);
步骤2:计算和当前第i个子片段序列相似的其他序列所占的比例以及与其他(Num-m)个子序列片段之间对应数据点之间的最大距离d[X(i),X(j)],总共需要计算Num-m次;
步骤3:将这Num-m个距离分别和给定的阈值r进行比较,当计算所得的距离小于阈值r时,被认为当前距离对应的两个子序列之间是相似的。对相似性序列个数进行计数,除以子片段序列总数Num-m,得到当前序列相抵的子序列的比例;
步骤4:上述结果是对一个子片段序列X(i)的相似性比例进行度量得到,对整个时间序列对应的所有子片段作分析得到该m个数据点规模下的子片段序列的平均相似率Bm(r);
步骤5:同理取子序列片段的长度为m+1,重复上述操作得到Bm+1(r);
步骤6:取两个平均相似率值的对数作差,得到原始序列信号的样本熵:
SampEn=lnBm(r)-lnBm+1(r)
(5)
SampEn的值受到m和r的值的影响,但因为样本熵本身的一致性比较好,因此其值不会由于m和r的影响,而变化较大。常常将嵌入维数m的值取1或2,相似度阈值r的值取原始序列标准差(SD)的0.2倍左右。本文取m=2,r=0.15SD。
1.3 粒子群优化算法优化的最小二乘支持向量机
粒子群优化算法(PSO)是一种基于群体智能的优化算法,其基本思想是通过群体中个体之间的信息传递和共享来寻找最优解。最小二乘支持向量机(LSSVM)是通过改进支持向量机(SVM)得到的,它不仅继承了支持向量机泛化能力强、全局最优等优点,而且克服了支持向量机计算复杂度高、运算速度慢的缺点。LSSVM预测时,惩罚参数c和高斯核函数中的参数σ对预测效果的影响显著。一般凭个人经验、实验对比、网格搜索法或者交叉验证等方法进行寻优,这些方法不仅效率低而且效果不佳。本文采用PSO来优化这两个参数,从而建立最优的LSSVM预测模型[8]。
1.4 基于EEMD-SE和PSO-LSSVM组合预测模型
由于要预测的原始序列往往表现出非稳定性,直接采用PSO优化的LSSVM预测模型进行预测,预测精度往往不高。如果对原始序列先采用EEMD分解,可以有效的降低原始序列的非平稳性。随着原始序列数据量的增大,EEMD往往会得到多个分量,预测的时间复杂度变大。采用样本熵可以整合这些分量,从而降低预测的时间复杂度。综上分析,本文提出基于EEMD-SE和PSO-LSSVM的PM2.5日均浓度组合预测模型,来对未来三天的PM2.5日均浓度进行预测。具体步骤如下:
步骤1:根据原始PM2.5日均浓度序列V={x1,x2,…xi,…,xn},其中xi表示在时刻i(i=1,2,…,n)的PM2.5日均浓度。选择一部分作为训练数据Vtrain={x1,x2,…,xn-s},另一部分作为测试数据Vtest={xn-s+1,xn-s+2,…,xn};
步骤2:对序列V进行EEMD,得到d个分量和一个剩余分量;
步骤3:利用样本熵对d个分量和剩余分量采用SE进行复杂度分析,并将复杂度相近的分量进行重组,得到d'个新序列;
步骤4:对d'个新序列分别建立LSSVM预测模型,利用训练样本的输入输出数据对模型进行训练,并利用PSO算法对LSSVM预测模型的惩罚参数c和核函数参数σ进行优化,得到d'个最优的LSSVM预测模型。分别对测试样本的输入数据进行预测,得到d'个预测结果;
步骤5:将d'个预测值叠加得到最终的预测值。
基于EEMD-SE和PSO-LSSVM的PM2.5日均浓度组合预测模型的预测流程如图1所示。

图1 EEMD-SE和PSO-LSSVM 组合预测模型流程图
2 实例分析
2.1 数据来源
本文采用上海某空气质量监测机构提供的2016年3月1日-2016年10月31日上海市PM2.5日均浓度数据,共233个数据。选取前230个数据作为训练数据,其PM2.5日均浓度时序图如图2所示,后3个数据作为测试数据。
从图2可以看出,该时间段上海市的PM2.5日均浓度整体上呈下降趋势,波动非常明显,相邻两个时间点的浓度值有些相差很大,呈现出不稳定性。特别是图2中虚线框所示的时间段,PM2.5日均浓度刚开始处于高水平,然后突然降低到低水平,之后又突然升高到高水平,这说明PM2.5日均浓度变化比较突然,这是可能是由于气候因素和人为因素(工业污染、汽车尾气排放)等引起的。综上所述,PM2.5日均浓度序列表现出不稳定性,这也给预测精度带来影响。
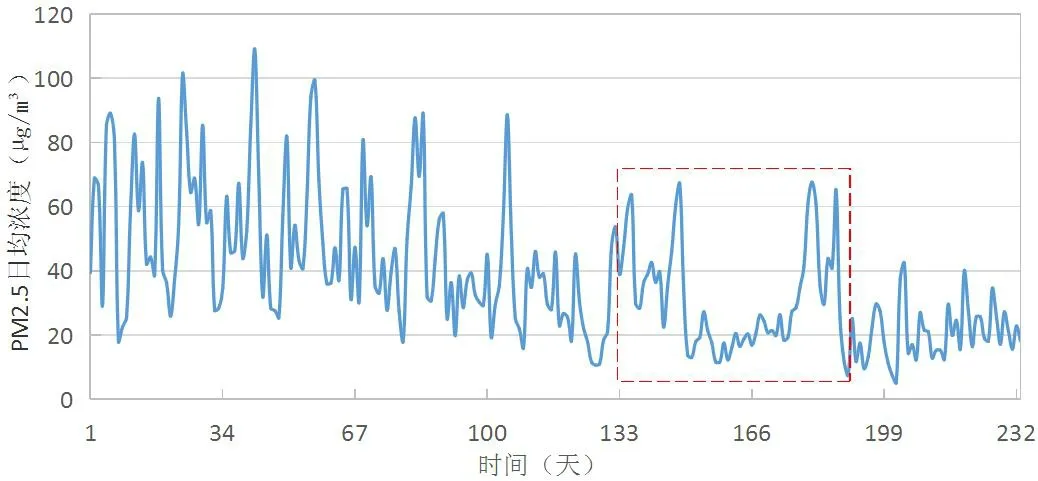
图2 上海市PM2.5日均浓度时序图
2.2 使用EEMD对原始序列进行分解
为了提高预测精度,使用EEMD对原始序列进行分解,产生多个相对稳定的子序列。利用MATLAB软件实现EEMD,共得到6个IMF分量IMF1~IMF6和一个剩余分量,如图3所示。
从图3可以看出,EEMD得到的7个分量的变化范围明显小于原始序列的变化范围。其中,剩余分量是趋势分量,呈现出单调递减的趋势,与PM2.5日均浓度整体呈下降趋势相同;其余6个分量是随机分量,IMF1、IMF2、IMF3的波动频率较大,IMF4和IMF5的波动频率一般,IMF6的波动频率较小。尽管这些分量的波动频率不同,但是可以看出,除了IMF6和剩余分量,其余分量的数据点几乎分布在数值零的上下两侧,表现出一定的均匀性。为了提高预测的效率,采用SE对上述7个分量进行重组。
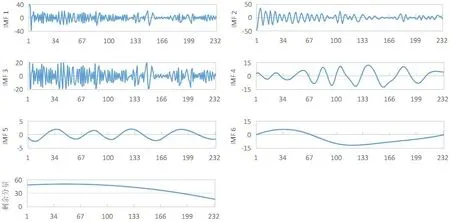
图3 PM2.5浓度序列EEMD结果
2.3 使用样本熵对EEMD分量重组
利用样本熵理论,计算图3中的7个分量的样本熵值,对分量进行复杂度评估,结果如图4所示。从图4可以看出,原始序列的样本熵值明显大于EEMD得到的7个分量的值,同时,IMF2和IMF3、IMF4和IMF5、IMF6和剩余分量的样本熵值非常接近。根据分量样本熵的分布情况,可以将IMF2和IMF3叠加得到一个新的序列,将IMF4和IMF5叠加得到一个新的序列,将IMF6和剩余分量叠加得到一个新的序列,如表1所示。

图4 序列及分量的样本熵

表1 各EEMD分量重组为新分量的结果
经过重组后的新序列在保留原分量特性的同时降低了计算复杂度,其变化趋势如图5所示。从图5可以看出,新分量SEIMF4反映了原始序列在整体上的变化趋势,是趋势分量;SEIMF1的波动频率与原始序列接近,但是变化范围小,反映了原始序列在细节上的变化趋势,是细节分量;SEIMF2和SEIMF3反映原始序列由于不可知的原因(如气候和人为因素)造成的波动,是随机分量。新分量较原始序列稳定,较EEMD得到的分量个数少。

图5 重组后新分量浓度时序图
2.4 PSO-LSSVM模型的参数优化
对重组后得到的四个新分量,分别建立PSO-LSSVM预测模型,其中,惩罚参数和核函数参数由PSO来优化,优化结果如表2所示。

表2 惩罚参数和核函数参数优化结果
2.5 预测效果评价
为了检验预测模型的适用性,利用均方根误差(RMSE)、平均相对误差(MRE)和平均绝对误差(MAPE),来对点预测结果进行评价分析。

(6)

(7)

(8)
式中:yi和y'i分别表示第i天的实测值和预测值;n表示样本总个数;M表示预测样本总个数;ymax表示测试样本实测值的最大值。RMSE反映了预测值的偏差,MRE反映了预测值接近实测值的程度,MAPE反映了预测值的整体误差。这三个指标的值越小,表明预测精度越高。
为了验证本文所提出模型,分别采用了PSO-LSSVM模型和时间序列常用的差分自回归移动平均模型(ARIMA(p,d,q))[9]进行预测来比较其效果。其中ARIMA(p,d,q)模型中,分别取不同的(p,d,q)值进行试验,以平均绝对误差作为评价指标,发现当自回归项p=1,移动平均项数q=1,差分次数d=1时模型预测效果最好。上述预测模型的预测结果如表3所示。

表3 三种预测模型的预测结果 (单位:μg/m3)
根据表3的预测结果,绘制预测曲线如图6所示。从表3和图6可以看出,本文提出的组合预测模型的预测结果的变化趋势与实测值相同,而且预测曲线与实测值曲线最接近。

图6 三种预测模型的预测曲线
进一步,计算三种预测模型的三个误差指标,如表4所示。表4显示了EEMD-SE和PSO-LSSVM模型的三个性能指标RMSE、MRE和MAPE的值分别为1.32 μg/m3、5.1%和5.7%,均低于其他两种模型的结果,说明本文提出的模型预测精度更高。同时,MRE和MAPE的值均低于6%,相关环保部门可以通过此模型来预测未来三天的PM2.5日均浓度,以便对可能发生的重度污染提前预警,进而调控社会活动。

表4 三种预测模型的预测误差对比
PM2.5严重影响了城市空气环境质量,为了准确的预测PM2.5日均浓度,本文提出了一种基于EEMD-SE 和PSOA-LSSVM的组合预测模型,来预测未来3天的PM2.5日均浓度。采用EEMD结合SE对数据进行预处理,EEMD降低了原始序列的不稳定性,SE减少了分量个数,整体上提高了运算效率;经过PSO优化的LSSVM预测模型能更加准确的对PM2.5日均浓度进行预测。实例证明了本文提出模型的有效性。

