双馈风机的小信号阻抗模型与稳定性

苏勋文, 岳 兵, 安鹏宇, 崔含晴

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

近年来的研究发现，风电场的变换器控制器与电网阻抗之间存在的耦合作用导致了风电场并网失稳。因此，在风电场并网时，电网具有弱电网特性，其阻抗不能忽略。在弱电网作用下，风电场阻抗和电网阻抗的相互影响是系统失稳的主要原因[1]。

阻抗分析法在双馈风机稳定性的研究上应用较少，直到最近五年才有相关文献对其进行等效建模分析[2-5]。I. Vieto等[6]在旋转坐标系下,建立了考虑电流控制器、锁相环以及定转子匝数比的双馈风机的序阻抗模型。张学广等[7]构建了考虑电机自身定转子磁链暂态的双馈风机转子侧等效导纳模型，分析了弱电网条件下控制参数对系统稳定性的影响。方冉[8]在dq坐标系下给出了双馈风机的统一阻抗模型，转子侧变换器采用了以有功和无功功率作为d轴和q轴输入量的功率控制策略，但未考虑杨晨华[9]以无功作为d轴输入量、有功作为q轴输入量的控制策略。笔者采用阻抗分析法在dq坐标系下建立双馈风机完整的导纳模型，推导双馈风机的小信号导纳公式，仅采用以输出的无功功率作为d轴输入量的功率控制策略，在Matlab/Simulink软件中对双馈风机建模，验证导纳模型的正确性，在弱电网条件下，分析控制器参数的变化对双馈并网系统稳定性的影响。

1 转子侧变换器的小信号阻抗建模

1.1 双馈电机的等效数学模型

假设双馈电机的定转子在空间上是对称分布的，且不计励磁饱和的影响，以电流流入为正方向，双馈电机在dq坐标下的等效电路如图1所示。

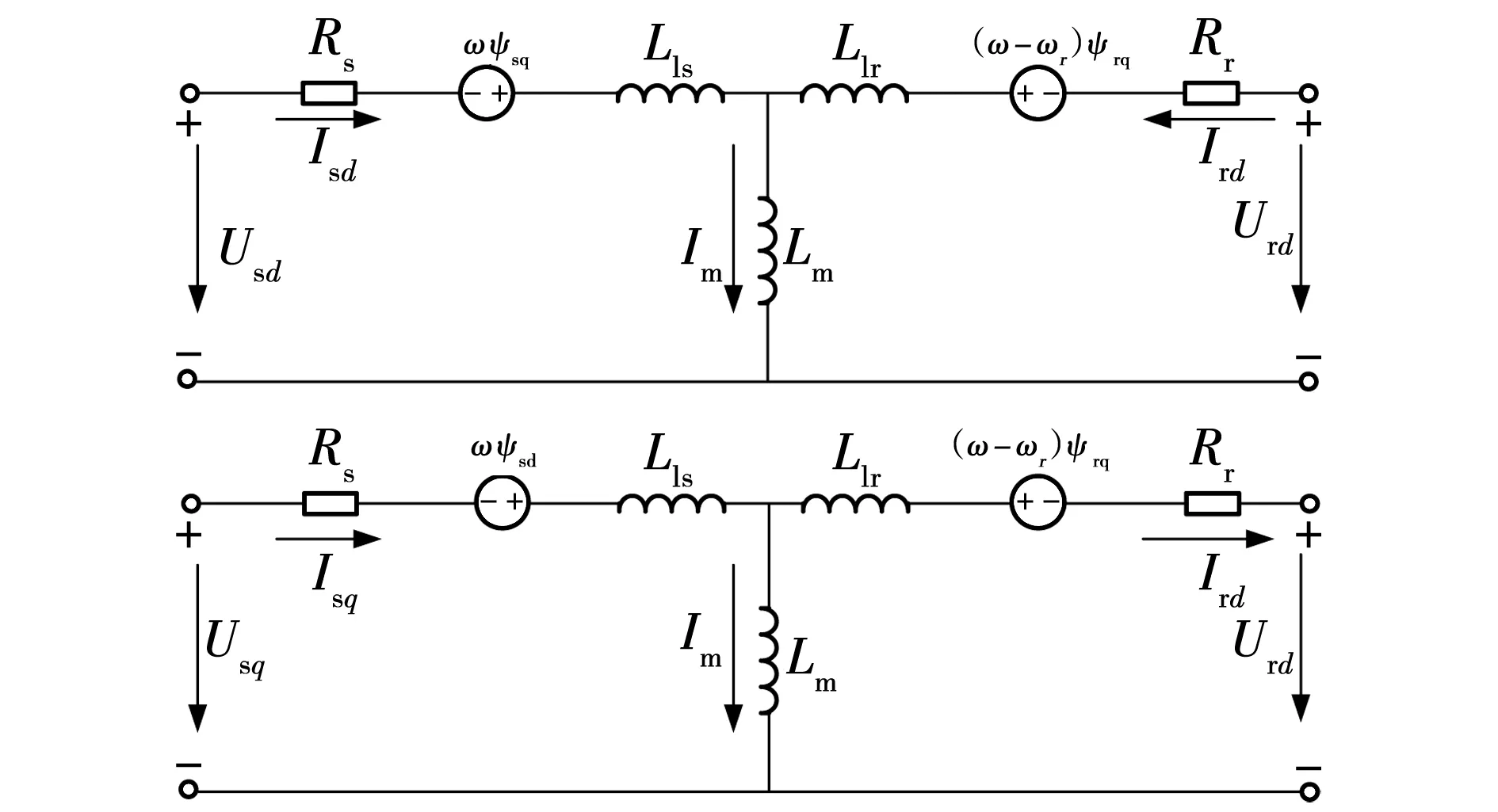
图1 双馈电机在dq坐标系下的等效电路 Fig. 1 Equivalent circuit of doubly-fed motor in dq coordinate system

在图1dq坐标系下，对物理量Us、Ur、Is和Ir引入小信号量，可以得到双馈电机的小信号公式为

(1)

式中：Gs、Gr——定、转子侧阻抗；

Gms、Gmr——定转子侧漏抗。

1.2 控制系统的建模

双馈风机转子侧变换器的控制器结构如图2所示。转子侧变换器采用定子磁链定量的矢量控制，是实现转子电流的解耦控制，可以对有功功率和无功功率进行单独控制。在整个控制器中，功率外环由无功功率控制d轴分量，内环由电流控制器构成，以转子电流参考为输入，以转子电压定值为输出。

图2 转子侧变换器控制器Fig. 2 Rotor-side converter controller

由图2可以得到，电流环的数学表达式为

(2)

式中:ird0、irq0——d和q轴分量的转子电流参考值；

kpr、kir——电流控制环节的比例和积分系数；

durd、durq——解耦项。

将式(2)作小信号处理并写成矩阵形式：

ΔUr=Gir(ΔIr0-ΔIr)+Gd1ΔIs+Gd2ΔIr，

(3)

式中：Gir——电流控制器的传递函数矩阵；

Gd1、Gd2——定转子电流解耦的传递函数矩阵。

转子侧变换器的功率外环控制器仅由无功功率控制d轴分量。根据图2可以得到，转子侧变换器外环控制器的数学表达式为：

Ird0=(Q0-Q)(kpq+kiq/s)+didr，

(4)

式中：didr——引入的前馈项，didr=-Uqs/ωLm；

Q0、Q——无功功率参考值和双馈电机输出的无功功率；

kpq、kiq——功率控制的比例系数和积分系数。

将式(4)经过小信号处理后，可得：

ΔIr0=-GqrΔQ+Gd3ΔUs，

式中：Gqr——功率控制器的传递函数矩阵；

Gd3——前馈项的传递函数矩阵。

无功功率采用瞬时计算理论得出，其无功功率的小信号表达式为

ΔQ=GqiΔUs+GqvΔIs，

式中：Gqi——瞬时功率的电流矩阵；

Gqv——瞬时功率的电压矩阵。

在双馈风机系统中，锁相环的作用是使系统dq坐标系与控制器dq坐标系保持同步。图3为dq坐标系下的锁相环模型。

图3 两相旋转坐标系下的锁相环模型Fig. 3 PLL model in two-phase rotating coordinate system

由图3可以推出，锁相环输出角的小信号公式为

式中，HPLL=kpp+kip/s。

定义锁向环矩阵

通过推导得到系统dq坐标系与控制器dq坐标系之间的电压、电流传函矩阵分别为

在双馈风机系统中，定转子电流和电压可以通过以下传函矩阵在系统dq坐标系和控制器dq坐标系之间相互转化为

式中:Gpus、Gpis——定子侧电压、电流经锁相环变换的传递函数矩阵；

Gpur、Gpir——转子侧电压、电流经锁相环变换的传递函数矩阵。

根据式电流内环控制器、功率外环控制器和锁相环的小信号数学模型，可以得到转子侧变换器小信号阻抗模型：

(5)

Gd4=Gir(Gd3Gpus-GqrGqiGpus-GqrGqvGpis-Gpir)+

Gd2Gpir+Gd1Gpis-Gpur，

式中，Gd4——并网点电压扰动到转子电压的传递函数矩阵。

2 网侧变换器的小信号阻抗模型

已知网侧变换器在系统dq坐标系且没有控制电路影响下的阻抗为

网侧变流器采用电网电压定向控制策略，其主要目的是稳定直流母线电容电压，控制变流器流过的有功功率。网侧变换器控制器的结构如图4所示，网侧变换器是由直流电压控制外环和电流控制内环构成。

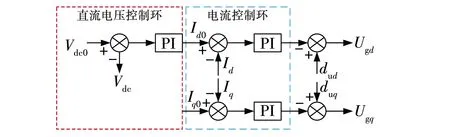
图4 网侧变换器控制结构Fig. 4 Control structure of grid-side converter

定义带有上标c的物理量为控制器dq坐标系下的物理量。由图4可见，电流内环控制器的数学表达式为

(6)

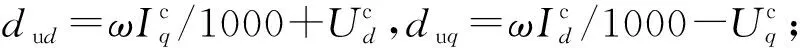
kpg、kig——网侧变换器电流控制环的比例系数和积分系数。

对式(6)作小信号处理，可以得到

(7)

式中：Gci——网侧电流控制器的传递函数矩阵；

Gd5——解耦项的传递函数矩阵。

网侧直流电压控制外环的作用为提供稳定的直流母线电容电压。此处直流电压控制环的q轴分量输出直接给定为0，那么根据图4可以得到，直流电压外环的数学表达式为

(8)

对式(8)作小信号化处理，可以得到

(9)

式中，Gdc——直流电压控制器的传递函数矩阵。

网侧变换器中，锁相环的动态影响与转子侧变换器是一致的，因此，电压、电流在系统dq坐标系与控制器dq坐标系之间转换关系为

根据式(7)和(9)的电流控制内环和直流电压控制外环的小信号模型，可以得到网侧变换器的小信号阻抗模型：

(10)

Gd6=(Gci+Gd5)Gpig，

式中，Gd6——并网点电压扰动到网侧控制器间的传递函数矩阵。

3 直流母线电容的小信号阻抗模型

直流母线电容连接着双馈风机的转子侧变换器和网侧变换器。由于直流母线电压的稳定性将会影响双馈系统的稳定性，因此需要建立直流母线电容环节的小信号阻抗模型。现假设流经转子侧变换器上的功率为Pr，流经网侧变换器上的功率为Pg，直流母线电容为Cm，根据能量守恒定律，可以得到

(11)

转子侧变换器功率Pr和网侧变换器功率Pg通过瞬时功率理论进行计算，其计算式为

(12)

将式(11)与(12)作小信号处理，得到

(13)

4 双馈风机的完整导纳模型与验证

将推导的双馈风机转子侧变换器、网侧变换器和直流母线电容的小信号阻抗模型式(5)、(10)、(13)联立，写成矩阵形式为：

(14)

Gk=GirGqrGqv-Gdl,

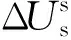
G-1D第1行和第2行双馈风机转子侧部分的等效导纳，记为YRSC；第7行和第8行为双馈风机网侧变换器的等效导纳，记为YGSC，那么双馈风机的等效导纳为

YDFIG=YRSC+YGSC。

将采用频率扫描法对双馈风机的小信号导纳模型进行验证。在Matlab/Simulink仿真中搭建双馈风机并网系统模型，同时对双馈风机的等效导纳进行扫描测量。图5为扫频结果。

图5 双馈风机并网系统扫频结果 Fig. 5 Frequency sweep results of grid-connected system of double-fed fans

由图5可知，由于考虑了磁链，四个通道在50 Hz处存在尖峰。dd通道和qd通道的导纳在低频段随频率增大而增大，但变化幅度不大，在高频段随频率增大而减小。dq通道和qq通道导纳在低频段随频率增大而减小，在高频段随频率增大先增大后减小。双馈风机仿真模型与双馈风机小信号导纳公式的扫频结果基本吻合，说明推导得到的双馈风机小信号导纳公式是正确的，可以应用于接下来的稳定性分析中。

5 控制参数对双馈风机稳定性的影响

文中涉及到的阻抗模型是建立在dq坐标系上的，是多输入-多输出系统，等效阻抗模型均以二阶矩阵的形式存在，此时需要通过广义奈奎斯特稳定判据对系统的稳定性进行判断。通过判断回比矩阵H(s)=G1(s)G2(s)的广义奈奎斯特曲线是否围绕(-1,j0)点来判断系统的稳定性，一般情况下，H(s)为电网阻抗与源阻抗的比值。若H(s)的广义奈奎斯特曲线不围绕(-1,j0)点，则系统是稳定的；反之，系统不稳定。

定义电网阻抗为

式中：G1(s)——电网阻抗；

G2(s)——双馈风机的导纳矩阵。

根据所建立的双馈风机小信号导纳模型，分析弱电网条件下双馈风机系统的稳定性。 文中在Matlab/Simulink中建立了容量为1.5 MW、额定电压0.4 kV的双馈风机模型。转子电阻和漏感分别为0.220 5和0.000 991(标幺值)，转子侧功率外环比例系数和积分系数分别为0.01和0.000 1，电流内环比例系数和积分系数均为0.02。定子电阻和漏感分别为0.214 7和0.000 991，网侧直流外环的比例系数和积分系数分别为2.5和0.5，电流内环比例系数和积分系数分别为3.0和0.1，锁相环的比例系数和积分系数分别为180和3 200。

图6为在上述参数下的双馈风机广义奈奎斯特曲线。由图6可知，广义奈奎斯特曲线没有包围(-1,j0)点，可以说明双馈风机系统是稳定的。

5.1 转子侧电流控制器参数

在双馈风机转子侧变换器中，电流控制器的dq轴采用相同的PI值。转子侧变换器电流控制器比例系数改变后的广义奈奎斯特曲线如图7所示。

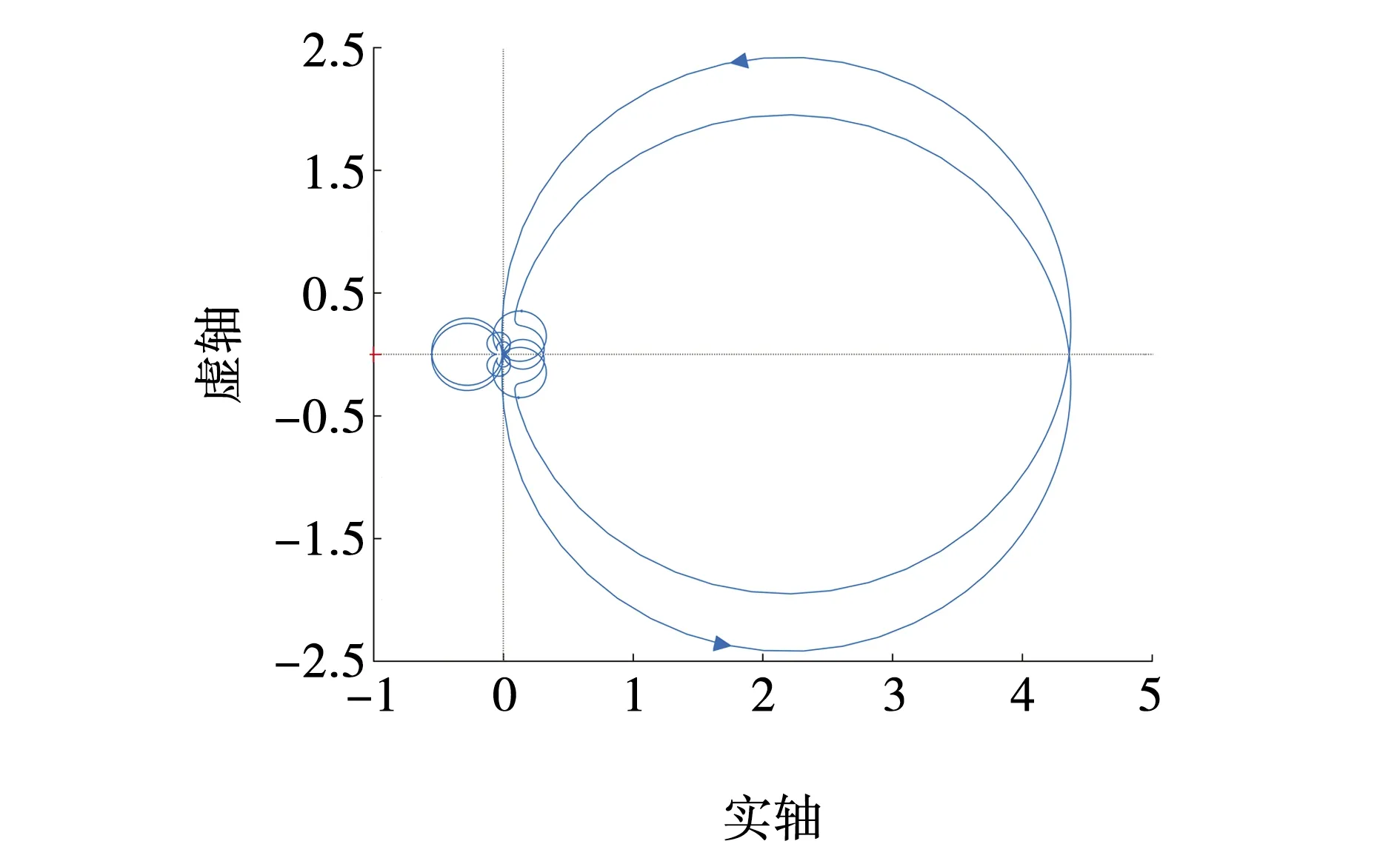
图6 双馈风机系统稳定时的广义奈奎斯特图Fig. 6 Generalized Nyquist diagram of a doubly-fed fan stable system

图7 转子侧变换器电流控制器的广义奈奎斯特曲线Fig. 7 Generalized Nyquist curve of rotor-side converter current controller

由图7可知，电流控制器的比例系数由0.02增大到0.08，再增大到0.2后，广义奈奎斯特曲线逐渐包围(-1,j0)点。根据广义奈奎斯特稳定判据，系统将从稳定过渡到不稳定的状态。这也说明了转子侧变换器的电流控制器比例系数增大将使系统失去稳定。

5.2 转子侧功率控制器参数

为了研究转子侧功率控制器参数变化对系统稳定性的影响，改变功率控制器的比例系数后得到的广义奈奎斯特曲线如图8所示。

图8 转子侧变换器功率控制器广义奈奎斯特曲线Fig. 8 Generalized Nyquist curve of rotor-side converter power controlle

由图8可知，功率控制器比例系数由0.000 1增大到0.1，增大100倍后广义奈奎斯特曲线仍然没有包围(-1,j0)点，这说明功率控制器参数的变化对系统稳定性的影响不大。

5.3 网侧电流控制器参数

网侧电流控制器参数改变后得到的广义奈奎斯特曲线如图9所示。网侧电流控制器的比例系数由3增大到6，再增大到12。

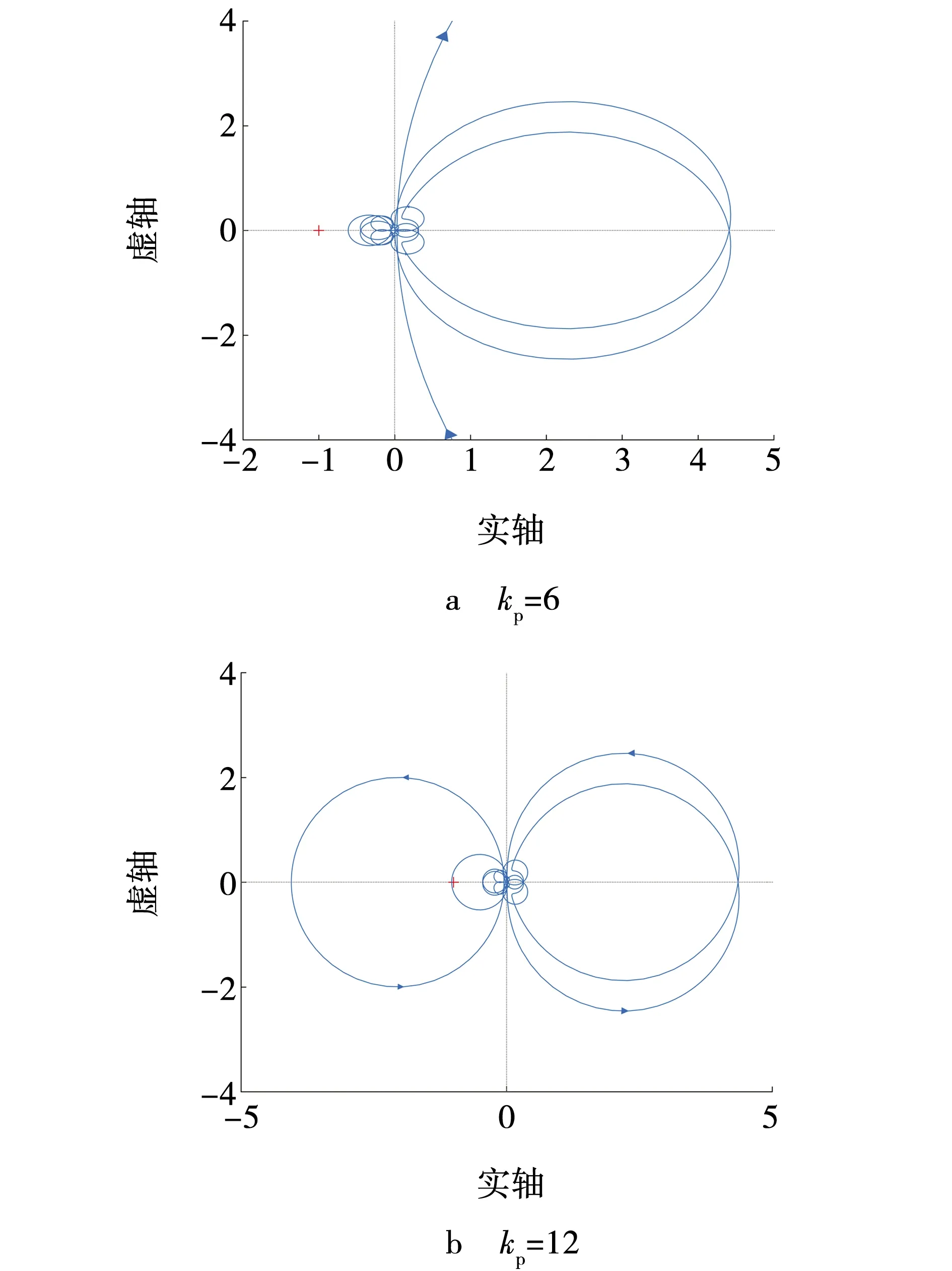
图9 网侧变换器电流控制器广义奈奎斯特曲线Fig. 9 Generalized Nyquist curve of grid-side converter’s current controller

由图9可知，网侧电流控制器的比例系数由3增大到6，再增大到12后，广义奈奎斯特曲线从不包围(-1,j0)点到包围该点，根据广义奈奎斯特稳定判据，说明网侧变换器电流控制器的比例系数增大将会使双馈风机并网系统失去稳定。

5.4 锁相环参数

锁相环的参数改变后得到的广义奈奎斯特曲线如图10所示。

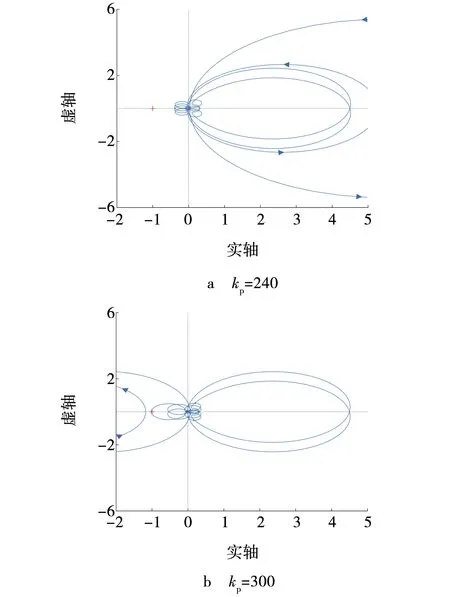
图10 锁相环比例系数广义奈奎斯特曲线Fig. 10 Generalized Nyquist curve after phase-locked loop proportional coefficient

由图10可知，锁相环比例系数从180增加到300后，广义奈奎斯特曲线从不包围(-1,j0)点到包围该点，根据广义奈奎斯特稳定判据，说明锁相环比例系数增大将使双馈风机并网系统逐渐失去稳定。

6 结束语

运用阻抗分析方法在dq坐标系下建立了完整的双馈风机小信号导纳模型，推导了双馈风机的小信号等效导纳公式，在Matlab/Simulink中通过频率扫描法测量了双馈风机的等效导纳，验证了导纳公式的正确性，说明了转子侧变换器的改进控制方式是可行的。同时，在弱电网条件下分析了转子侧和网侧控制器参数变化对系统稳定性的影响，通过广义奈奎斯特图可以看出，在双馈风机并网系统中，转子侧变换器和网侧变换器的电流内环和锁相环的比例系数增大可能会使系统失去稳定，而转子侧变换器的功率外环对系统稳定性影响不大。因此，在进行双馈风机并网的过程中，应该选择合适的控制器参数来保证并网系统能够稳定运行。