基于实体嵌入和长短时记忆网络的入侵检测方法*

赖训飞，梁旭文，谢卓辰，李宗旺,4

(1 中国科学院上海微系统与信息技术研究所， 上海 200050； 2 上海科技大学信息学院， 上海 201210；3 中国科学院上海微小卫星工程中心， 上海 201203； 4 中国科学院大学, 北京 100049)(2019年1月25日收稿； 2019年4月3日收修改稿)

随着互联网的发展，网络的规模越来越大，随之出现的网络攻击也越来越多，给计算机设施的安全性和敏感数据的完整性带来严重威胁。因此，网络入侵检测越发受到重视，成为国内外研究的热点之一。网络入侵检测主要是通过提取反映网络状态特征的数据，设计检测模型对正常和攻击的数据进行分类[1]。然而，在真实环境中采集到的网络特征数据基本是一种具有分类变量特征的结构化数据[2]，即是指以表的形式收集和组织的数据，列代表不同的特征属性，行代表不同的样本，结构化数据中最常见的是数值变量和分类变量。在衡量网络流量入侵模式数据的特征[3-4]中，表示连接持续时间、传送字节数、访问控制文件的次数等连续变量特征可以用数值表示，但是，还有许多特征只能以分类变量形式提供元数据，没有表征它们自己的信息，这些分类变量涉及表示协议类型(TCP、UDP、ICMP)、网络服务的类型、网络连接状态等特征属性。

近年来，由于大数据和高性能计算机平台的推动，深度学习成为入侵检测领域越来越重要的研究方法，深度学习将特征提取和分类器结合到一个框架中，能够自动从海量数据中去学习特征，给海量、高维数据的复杂分类问题提供非常有效的途径。为了学习网络状态特征前后之间的相互依赖关系，将表征网络状态特征的数据时序建模，在Tang等[5]和Yin等[6]提出的递归神经网络(recurrent neural networks, RNN)模型中，提高检测准确率的同时，还通过在模型的隐藏节点之间对数据特征进行局部关联，从而极大地减小了模型规模。但是RNN模型中存在梯度消失问题，很难长期学习保存信息。为了学习网络状态之间的长期依赖性，Staudemeyer[7]提出将网络流量建模为一个具有监督学习方法的时间序列，训练长短时记忆网络(long short-term memory network,LSTM)，实验在KDD Cup 99数据集上，验证了LSTM网络通过对网络状态特征数据的时序性和依赖性学习，可以有效地处理高维的表征网络状态特征的大数据。

为了在网络入侵检测模型中合并网络入侵数据中分类变量，近年来提出一些网络入侵检测算法，如Tang等[8]提出基于流量的异常检测深度神经网络模型，Vinayakumar等[9]提出一种卷积神经网络检测模型等。在这些深度学习算法中，数据预处理时，对网络入侵数据中分类变量的处理方法都是使用One-Hot编码[10]对分类变量进行转换，也称为One-of-k模式，即k个不同类别创建k个新的二进制特性，其中只有一个值是1，归一化后形成数据的输入。这种方法虽然解决了分类器不好处理分类变量数据的问题，也起到了扩充特征的作用，数据预处理后，使得检测模型达到了一定的检测效果。可是对于许多高基数特性的分类变量特征来说，One-Hot编码会使得特征空间变得很大，从而产生大量的稀疏数据，导致计算资源的浪费；其次，One-Hot编码对待分类变量的不同值是完全独立的，往往忽略了它们之间的信息关系。实体嵌入是一种将分类变量映射到欧几里得空间[11]，在一个神经网络中标准监督学习的过程，嵌入后得到的数据维度低，不仅能够将离散的序列映射成为连续的向量，还能够深度挖掘变量之间的关系。与One-Hot编码相比，实体嵌入不仅减少了内存的使用，加快了神经网络的计算速度，在数据稀疏且统计量未知的情况下，实体嵌入还能更好地帮助神经网络进行泛化。

基于以上分析，为了克服传统方法对网络入侵数据中分类变量处理的缺点，本文将实体嵌入的方法应用于网络入侵检测，同时结合深度学习中LSTM网络在入侵检测中处理高维、海量数据的优势[12]，提出一种基于实体嵌入和LSTM相结合的方法。数据预处理时，使用分类变量数据学习实体嵌入，其中每个分类变量都映射到一个固定大小的向量空间，然后使用神经网络模型学习参数。本文的神经网络模型采用LSTM网络，将数值变量数据输入与分类变量数据输入结合在一起，然后将这两个输入连接起来并馈送到LSTM网络训练检测模型，使得设计的LSTM网络达到最优检测效果。通过在NSL-KDD数据集[13]上进行实验验证，先预设分类变量的嵌入维度，通过调整LSTM网络的隐藏节点数和学习率，得到一个相对较优的LSTM网络，然后对比One-Hot编码对网络流量入侵数据中分类变量的预处理方法，验证实体嵌入对网络入侵数据中分类变量处理的有效性，同时，结合LSTM网络设计出一种网络入侵检测模型，提高了检测的准确率。

1 本文算法

1.1 实体嵌入

实体嵌入(entity embedding，EE)是将函数近似问题中的分类变量映射到欧几里得空间，这种映射是在一个神经网络中的标准监督学习过程。神经网络环境下实体嵌入方法的第一个领域是关系数据的表示[14]。近年来，大量复杂关系数据集合知识库中出现了大量使用实体嵌入的工作[15], 重构数据的基本数据结构形式是(h,r,t),其中h和t是实体，r是关系，实体映射到向量，关系有时映射到矩阵[16]或者两个矩阵或者与实体在同一嵌入空间中的向量。

在函数近似问题中，给定一个函数如下

y=f(x1,x2,…,xn).

(1)

式中：(x1,x2,…,xn)为输入数据,y为标签输出值。

为了学习函数(1)的近似，实体嵌入通过将一个分类变量xi的状态映射到一个向量，即

(2)

向量空间的大小，即嵌入层的维度[17]是需要预先定义的超参数。实体嵌入维度的边界在1和(mi-1)之间，其中mi是分类变量xi的所有状态的个数。在实践中，根据经验选择嵌入层的维度尺寸，采用经验准则:越复杂的维度越多。需要粗略估计描述实体可能需要多少特性，并将其作为开始的维度。

在深度学习处理结构化数据[18]过程中，学习嵌入的方法来表征数据特征时，首先，需要将结构化数据分为数值型和分类型变量，然后对分类型变量进行实体嵌入，在使用实体嵌入表示所有分类变量之后，所有嵌入层和所有连续变量的输入被连接起来。合并层被视为神经网络中的一个普通输入层[19]。整个网络可以用标准的反向传播方法进行训练。通过这种方式，实体嵌入层能够了解每个类别的内在属性，而更深层次的实体层形成它们的复杂组合。学习嵌入的具体步骤如下：

1) 对于每个分类型变量xi，创建一个实体嵌入矩阵m×L,其中m表示分类型变量xi的特征属性基数，L表示分类变量xi的嵌入维度，其中1≤L≤m-1。下面式(3)中矩阵表示的是一个分类型变量xi中所有状态的向量表示，其中每一行表示一种状态在嵌入空间中的映射

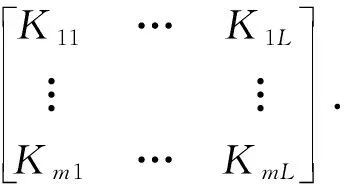
(3)

采用相同的方式可以得到每个分类型变量的数据向量表示。

2) 通过在嵌入矩阵中查询给定分类变量的状态就能得到所有分类变量的向量表示，然后把它嵌入到数值型变量的数据后面，组成全新的数据输入。

3) 定义一个神经网络，然后把每一组数据都输入到神经网络去训练，为使损失函数最小，可以通过在神经网络反向传播过程中梯度的变化不断地更新分类变量型数据的嵌入矩阵，使得每次数据迭代后都能够获得更好的嵌入表示，从而优化嵌入的映射。

1.2 长短时记忆网络

本文针对网络入侵检测中的高维、海量的网络特征数据，采用长短时记忆网络LSTM[20]进行训练，LSTM是时间递归神经网络的一种变形，相比于传统的RNN模型，LSTM对隐藏层做了更复杂的设计，其核心设计是一种叫做记忆体(cell state)的信息流，如图1所示，它负责把记忆信息从序列的初始位置传递到序列的末端，并通过4个相互交互的“门”单元，控制在每一时间步t对记忆信息值的修改。LSTM这种隐藏层的逻辑设计可以有效地保留长时间的记忆信息，避免了梯度消失的缺点。

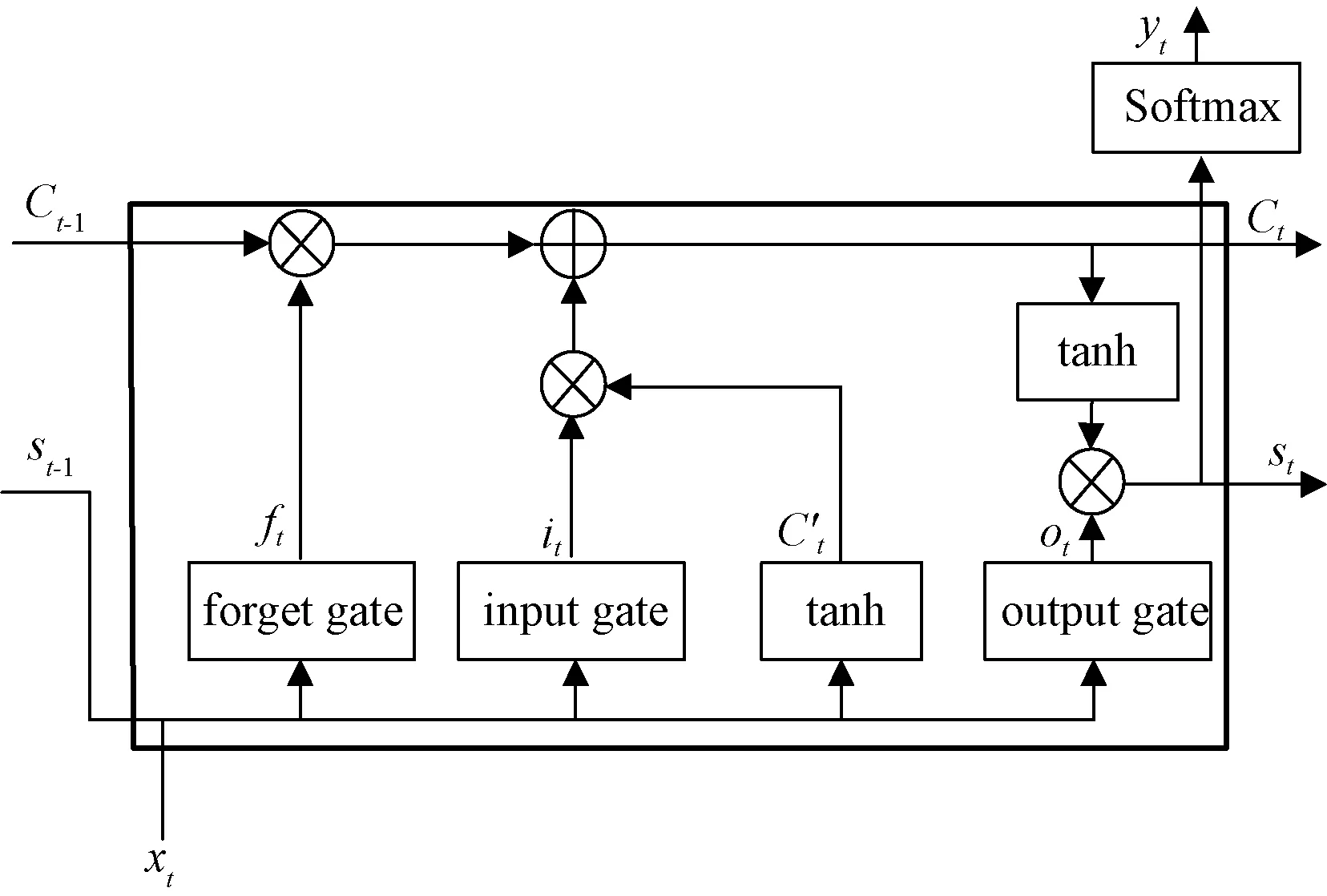
图1 LSTM隐藏层的逻辑设计结构Fig.1 Logic design structure of LSTM hidden layer

在记忆体的信息流中，遗忘门控制着前面记忆中丢失信息的多少；输入门决定第t时间步的输入信息xt，有多少信息将被添加到记忆信息流中；候选门用来计算当前的输入与过去的记忆所具有的信息总和量；输出门控制着有多少记忆信息将被用于下一阶段的更新中。

将图1所示的LSTM隐藏层逻辑单元，多个连接在一起形成一个LSTM网络模型。本文针对网络入侵检测，采用的是一个“多对多”型结构，即多个输入的同时有多个输出，如图2所示。模型的训练主要包含前向传播和反向传播过程。

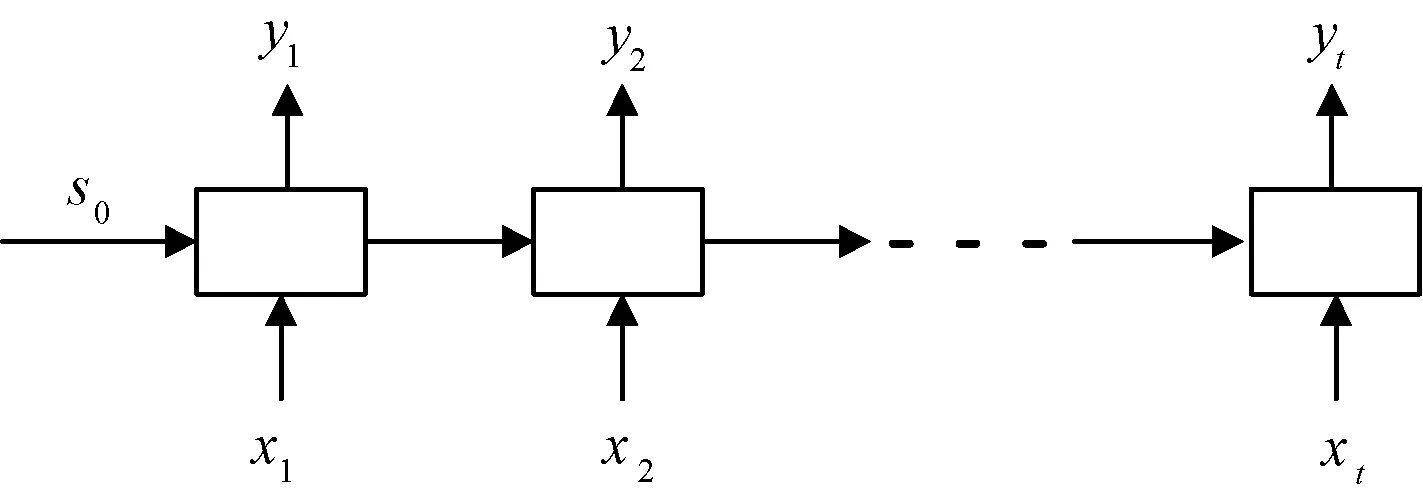
图2 LSTM网络结构Fig.2 LSTM network structure

其中LSTM网络模型训练的具体算法过程如下：

前向传播过程：记输入时间序列为X=(x1,x2,…,xt),隐藏层序列为S=(s1,s2,…,st),则通过迭代公式计算预测输出序列Y=(y1,y2,…,yt)的计算过程如下：

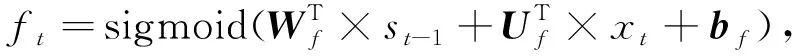
(4)

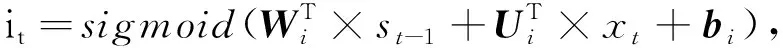
(5)

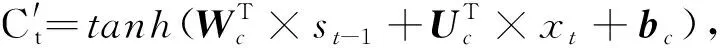
(6)

Ct=ft×Ct-1+it×C′t,

(7)

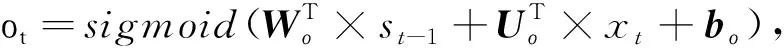
(8)

st=οt×tanh(Ct),

(9)

yt=softmax(VT×st+c).

(10)

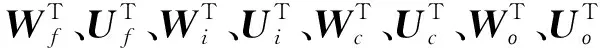
反向传播过程：采用时间反向传播算法来训练参数，主要是通过叠加每个时间步的参数梯度来更新参数，损失函数是计算每个时间步预测输出层的交叉熵，在第t个时间步时，损失函数的计算过程为

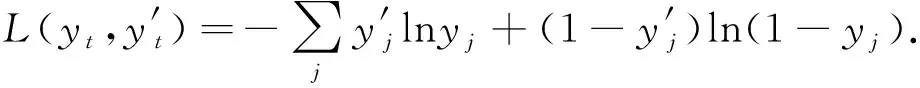
(11)

式中：yt是预测输出，y′t是输出的真实值，j表示预测输出层的第j神经元。

在每一次迭代中，参数矩阵通过式(12)来更新：

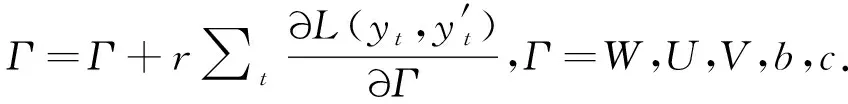
(12)

式中：r是学习率，时间步t=0,1,…,T.

2 网络入侵检测模型

本文基于实体嵌入和LSTM网络的方法建立的入侵检测模型流程如图3所示，主要分3个部分：数据预处理、模型训练、模型测试。

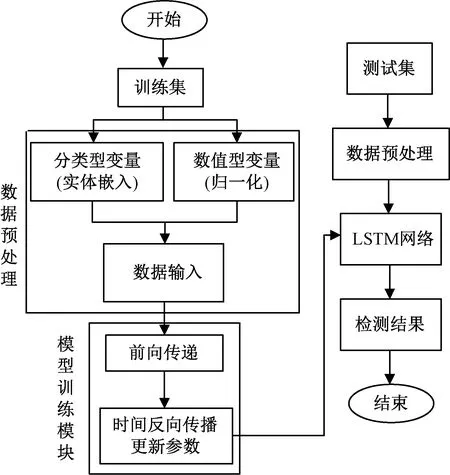
图3 网络入侵检测模型Fig.3 Network intrusion detection model

入侵检测模型检测的具体步骤如下：

1) 数据预处理

在数据预处理过程中，首先，需要将训练集的每一个数据中的分类型和数值型特征属性的数据分开。对数值型的数据，需要进行归一化处理，处理方式如下

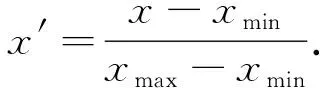
(13)

式中：xmax和xmin分别表示x所在列中的最大值和最小值，x′为x归一化后的数据。

然后，对于分类型的数据，根据嵌入的维度映射成为一个向量。在所有的分类变量都用实体嵌入的方法表示后，由每一个分类型数据表示的向量都连接到归一化后的数值型数据后面，组合成新的数据输入。

2) 模型训练

在所有的训练集中的数据都按照步骤1)转换成数据输入后，将数据时序建模，为了使得检测过程中具有关联数据的功能，模型训练采用的是一个“多对多”的循环神经网络。即多个LSTM逻辑单元连接在一起，形成一个LSTM网络。模型训练的过程，是一个学习嵌入的过程，同时也是一个得到最优检测模型的过程。因为在时间反向传播更新参数的过程中，不但是损失函数逐渐达到最小的过程，也是分类型数据的嵌入向量不断被更新，得到最优数据输入的过程。

3) 模型测试

根据步骤1)先对测试集进行数据预处理，得到数据输入，然后根据步骤2)中训练得到的LSTM模型，输入到模型中进行检测，得到检测结果。

3 数据集及评价方法

3.1 数据集描述

本文采用NSL-KDD数据集(下载地址https:∥www.unb.ca/cic/datasets/nsl.html)进行实验验证。该数据集是KDD Cup 99数据集(下载地址http:∥kdd.ics.uci.edu/databases/kddcup99/kddcup99.html)的改进和简化版本，KDD Cup 99数据集是来源于1998年美国国防部高级规划署在林肯实验室进行的一项为捕获网络流量数据而准备的入侵检测评估项目。训练用的网络流量数据被收集7周，测试用的网络流量数据收集了2周。KDD Cup 99数据集作为评价网络入侵检测系统的基准数据集已被广泛使用多年，然而该数据集的一个主要缺点是，它在训练和测试数据中都包含大量的冗余记录。为了克服KDD Cup 99数据集的局限性，提出NSL-KDD数据集，它改进了以前的数据集，使得NSL-KDD数据集中的总记录统计合理。

NSL-KDD数据集中每一种网络流量模式都由41个特征定义，这些特征包括直接从TCP/IP连接的基本特性、在窗口间隔(如2 s或多个连接)中累积的流量特性以及从连接的应用层数据中提取的内容特性。在表示网络流量数据的41个特征中，特征属性的类型可以分为离散型(symbolic，S)和连续型(continuous，C)，具体的特征属性描述如表1所示。

表1 数据特征属性Table 1 Data feature attribute

在表示网络流量入侵模式数据中的7个离散型特征都是分类变量，分别是Protocol_type，service，flag，land, logged_in,is_hot_ligin,is_guest_login，其中分类变量Protocol_type表示协议类型，共有3种：TCP、UDP、ICMP，特征属性基数为3；service表示目标主机的网络服务类型，共有70种，特征属性基数为70；flag表示连接正常或错误的状态，共11种，特征属性基数为11；land表示连接是否来自同一个主机/端口，特征属性基数为2；logged_in表示是否成功登录，特征属性基数为2；is_hot_ligin表示登录是否属于“hot”列表，特征属性基数为2；is_guest_login表示是否guest 登录，特征属性基数为2。

网络流量数据主要被标签为正常和4种不同类型的攻击流量，4种攻击分别是DoS、Probe、U2R和R2L攻击,其中DoS攻击会耗尽目标服务器的资源，使其无法提供任何服务；R2L攻击允许未经授权的远程访问；U2R攻击尝试获取超级用户权限；Probe探测攻击用于查找目标服务器的漏洞，如表2所示。

表2 数据类别Table 2 Data categories

3.2 评价方法

网络入侵检测算法的性能通过准确率AC、误报率FA和漏报率MA来衡量，它们的计算方法如下：

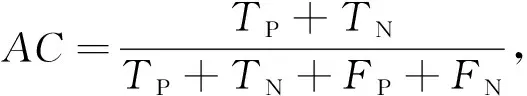
(14)

(15)

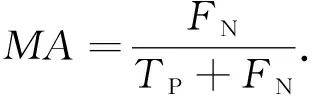
(16)

式中：TP代表正确分类的攻击记录，TN代表正确分类的正常记录，FN代表错误分类的攻击记录(漏报),FP代表错误分类的正常记录(误报)。

4 实验验证

实验包括100 000个训练样本和20 000个测试样本。实验样本的具体类型和个数如表3所示。

表3 实验数据Table 3 Experimental data

实验环境是window10 64位操作系统，Intel(R)core(TM) i7-6500U,CPU 2.5 GHZ,内存8.00 GB，采用GPU加速，在基于深度学习框架PyTorch下，Python语言编程实现。实验的具体参数为：权值初始化方式为随机初始化，损失函数为交叉熵，优化算法是SGD(随机梯度下降)，最大迭代次数为500， 批次大小为100，隐藏层dropout取0.2。

本文主要做了3组实验，第1组实验，针对网络流量数据中的分类变量，使用实体嵌入的方法，通过在3种预设规则下，得到分类变量的不同嵌入维度，目的是确定一个相对最优的实体嵌入的维度(L)；第2组实验，预设不同的隐藏节点数(H)和学习率(R)，目的是确定相对最优的LSTM网络参数；第3组实验，对比传统的对网络入侵数据中分类变量的处理方法，验证本文提出的实体嵌入方法对分类变量处理的有效性。

1) 确定嵌入层的维度

把网络流量数据中的离散型和数值型数据分开处理，离散型特征属性的数据作为分类变量，通过实体嵌入的方法处理后，和归一化后的数值型数据组合在一起后，得到数据的输入。每一个表示网络流量特征的41维数据中，表示分类变量的特征属性有7个，连续性数值型变量的特征属性有34个。根据实体嵌入理论，分类变量的嵌入维度是一个需要预先定义的超参数，在实践中，可以用经验准则来选择嵌入维度，即越复杂的维度越多，先粗略估计描述实体可能需要多少特性，并将其作为开始的维度。所以，在实验的过程中，根据经验，预先设定3种规则下的分类变量嵌入维度，当分类变量的特征属性基数为m时，嵌入维度为L，具体规则如下：

①当(m-1)<2时,L=2;

②当2≤(m-1)≤C，L=(m-1)，其中C为常数；

③当(m-1)≥C，L=C。

实验过程中，规则①取C=10；规则②取C=30；规则③取C=50；可以看到对于特征属性基数较少的分类变量land、logged_in、is_hot_ligin、is_guest_login和Protocol_type来说，嵌入维度不需要太复杂，所以，3个规则下的嵌入维度都是取2。但是对于分类变量service和flag,因为它们的特征属性基数比较大，需要较大的嵌入维度对其进行描述，所以，3种规则下，分类变量service的嵌入维度分别取10、30、50，分类变量flag的嵌入维度都是取10，具体如表4所示。

表4 特征属性基数以及嵌入维度Table 4 Feature attribute cardinality and embedding dimension

这里先设定隐藏层节点数H=30，学习率R=0.2进行实验，来确定一个相对最优的嵌入层维度，得到的实验结果如图4所示。可以看到，嵌入维度在3种规则下，准确率随着迭代次数的变化中，当迭代次数小于200时，规则①的嵌入维度下，检测模型得到准确率要比其他两种规则的准确率更低，迭代次数大于200时，随着曲线趋于稳定，规则①的嵌入维度下，检测模型得到准确率要比其他两种规则的更高，另外比较3种规则的嵌入维度下，检测模型的训练时间，分别是914、977和1 086 s。综合来看，规则①预设的嵌入维度相对最优，即分类变量Protocol_type、service、flag、land、logged_in、is_hot_ligin、is_guest_login的嵌入维度分别取2、10、10、2、2、2、2。此时，在使用实体嵌入表示所有分类变量之后，所有嵌入层和34个归一化后的数值型变量连接起来，合并成的输入数据的维度为64。

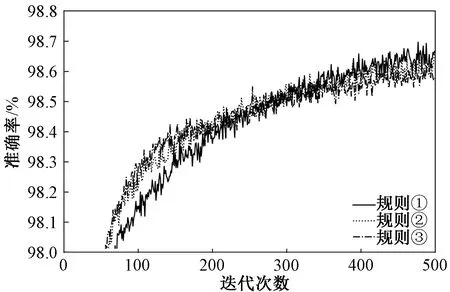
图4 不同嵌入维度下的迭代曲线Fig.4 Iteration curves under different embedding dimensions

2) 确定隐藏节点数H、学习率R

为了确定一个相对最优的LSTM网络，在相对最优的嵌入维度规则，即输入数据的维度为64时，隐藏层节点数分别取H=20、30、50，学习率分别取R=0.1、0.2、0.3，进行9组实验，实验结果如表5所示。综合来看，检测性能最好时，隐藏层节点数应该取20，学习率取0.3,此时模型的检测准确率最高，达到98.90%。

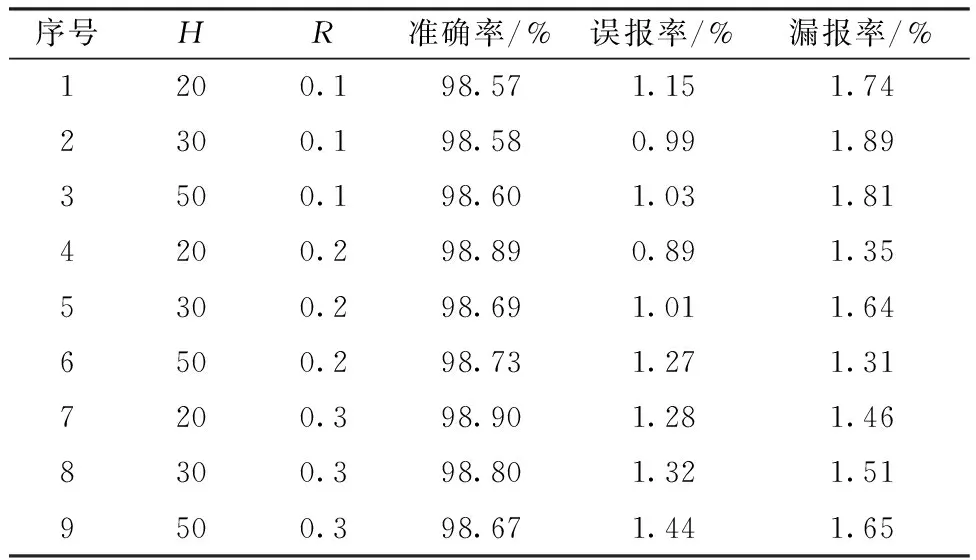
表5 不同参数的检测效果Table 5 Detection effects of different parameters

3) 对比实验

通过以上两组实验后，得到一个相对最优的检测模型。在最优检测模型下，为了验证算法模型的优越性，采用训练样本100 000个和20 000个测试样本总共120 000个数据样本，通过6折叠交叉验证的方式，得到入侵检测的各种评价指标。将本文基于实体嵌入和LSTM网络的检测方法 (EE-LSTM),与基于One-Hot编码和LSTM的方法(OH-LSTM)进行对比实验。

实验过程中，OH-LSTM检测方法是数据预处理时采用One-Hot的编码处理分类变量，数据归一化得到数据输入后，输入到LSTM网络中训练，选择的初始化方式、批次数、下降方式、损失函数都与EE-LSTM检测方法相同，其他参数通过调整得到相对最优的检测模型。

两种方法的迭代曲线如图5所示，另外还从两种方法的准确率、误报率、漏报率3个方面进行了对比，实验结果如表6所示。通过图5(a)和5(b)可以看到，随着迭代次数的增加，在迭代次数达到500时，采用两种方法的检测模型的准确率和损失函数值都趋于稳定，但是本文方法的准确率一直高于OH-LSTM的检测方法，损失函数值也一直低于OH-LSTM的检测方法。通过表6的数据可以看到，对比OH-LSTM的检测方法，EE-LSTM的检测方法在准确率上高出1.44个百分点，误报率降低0.04个百分点，漏报率降低2.99个百分点，从整体上验证了本文检测方法的优越性能。

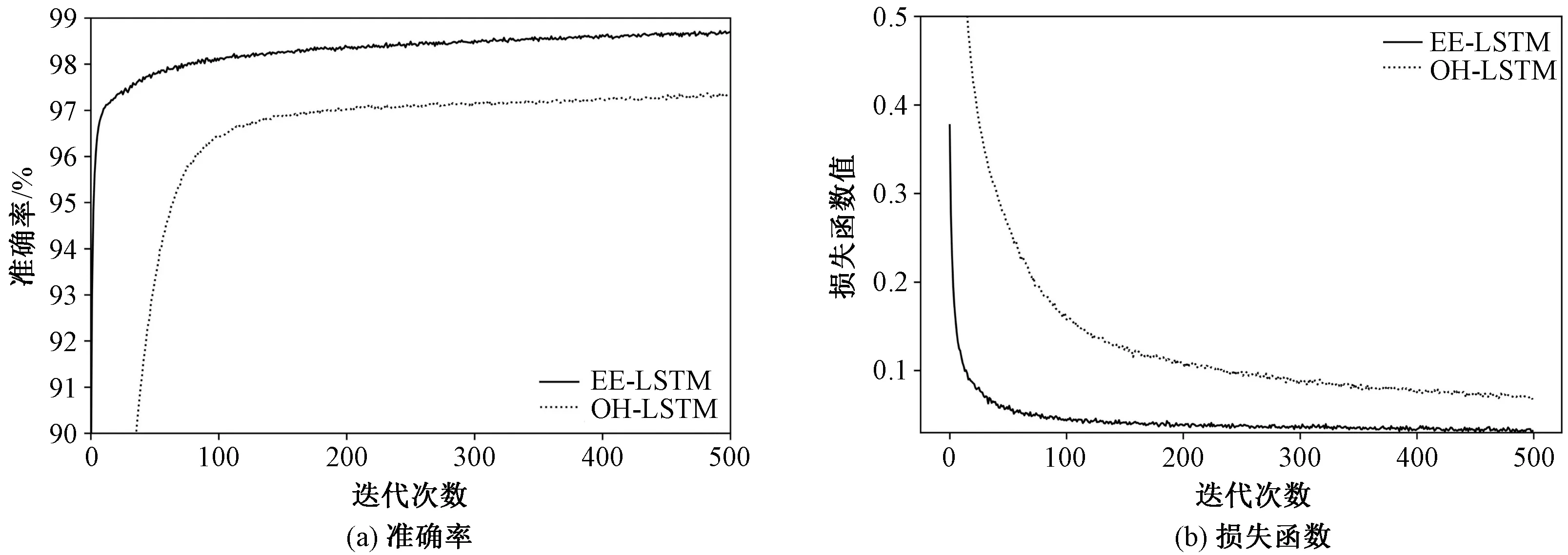
图5 准确率和损失函数随迭代次数变化Fig.5 Variations of accuracy and loss function with number of iterations

表6 两种检测方法的性能对比Table 6 Performance comparison between the two detection methods %

为进一步验证本文检测方法的良好检测性能，实验中将EE-LSTM和OH-LSTM两种检测方法对各类攻击的检测性能进行了对比，图6表示的是两种检测方法中对每一类攻击检测的准确率。

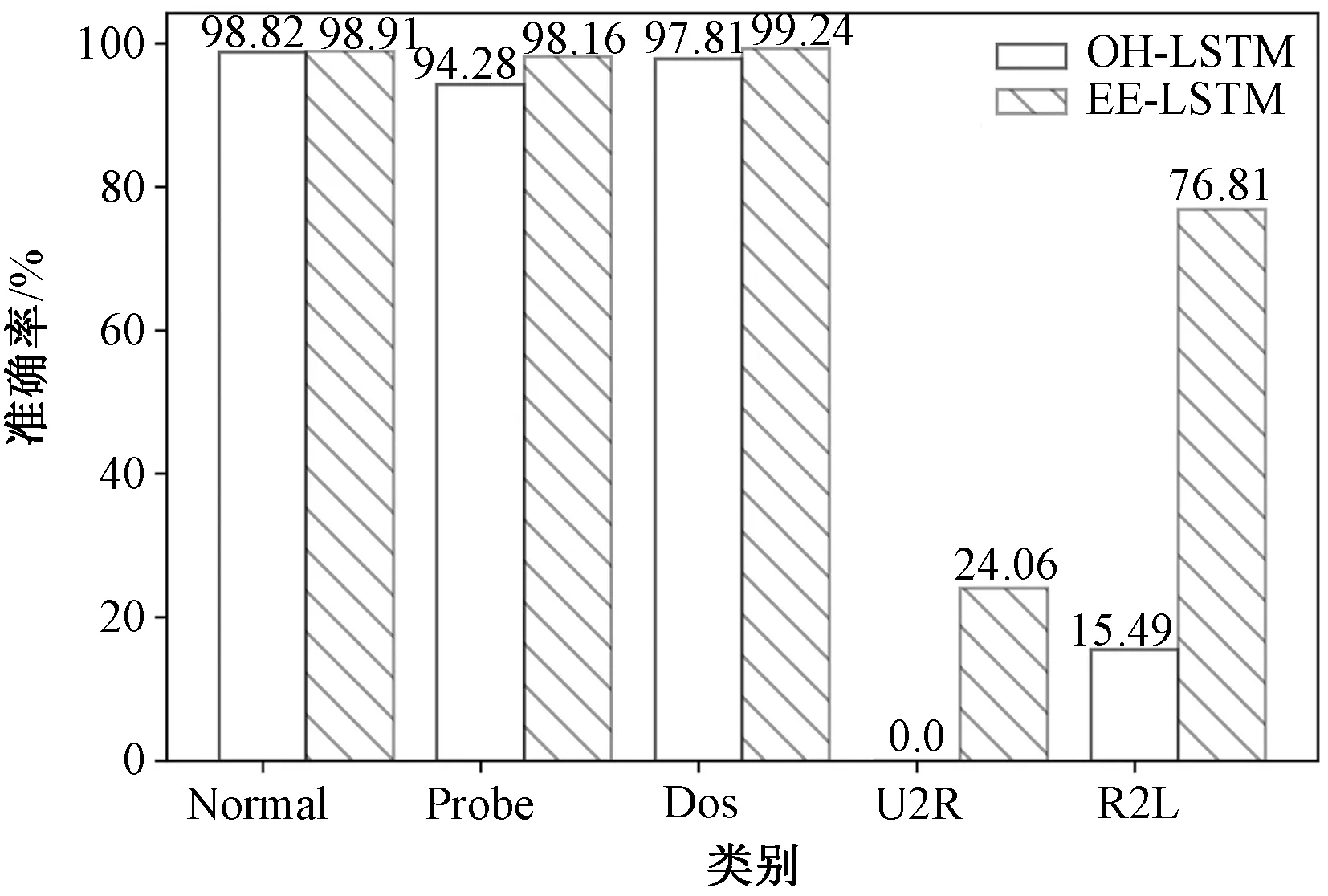
图6 不同数据类别的准确率对比Fig.6 Accuracy comparison among different data categories

通过图6可以清楚地看到本文的方法对每种攻击的检测率都要明显高于OH-LSTM的方法。对于DOS和Probe类型的攻击，本文方法检测的准确率接近100%。然而对于U2R和R2L攻击类型，因为样本数目太少的原因，一般情况下难以实现对U2R和R2L攻击类型的检测，甚至在OH-LSTM的检测方法中，U2R攻击类型没有被检测出来。但是，在本文方法中，对U2R和R2L的检测效果都很明显地高于OH-LSTM的方法。

5 结论

针对网络入侵检测中海量、高维的结构化数据，通过实体嵌入的方法对分类变量的处理，结合LSTM网络捕获网络特征数据的时序性和依赖性的优势，本文提出基于实体嵌入和LSTM网络的检测方法，将表征网络特征的结构化数据时序建模。在数据预处理时，对分类型变量特征属性进行实体嵌入，在使用实体嵌入表示所有分类变量之后，所有嵌入层和所有连续变量的输入被连接起来，合并层被视为神经网络中的一个普通输入层，在提出的LSTM网络中训练，使得输入数据能够更好地表征原来结构化数据的特征的同时，也得到了最优的检测模型。与传统的处理网络入侵数据中分类变量方法One-Hot编码相比，从对网络攻击的检测效果来看，结果表明，总体上本文提出方法具有更高的准确率，降低了误报率，还很明显地降低了漏报率，而且对小类攻击样本[21]的检测具有明显优势，为网络入侵检测数据中的分类变量提供了一种有效的处理方法；同时，结合深度学习中LSTM网络在处理高维大数据中的优势，为网络入侵检测领域提供一种新的检测方法。下一步工作是通过改变分类变量的嵌入维度，进一步优化检测模型。