An underwater mining navigation method based on an improved particle filter*
ZHANG Zhihui, FENG Yingbin, LI Zhigang, ZHAO Xiaohu,3
(1 State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China; 2 Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China; 3 University of Chinese Academy of Sciences, Beijing 100049, China)(Received 24 December 2018; Revised 4 March 2019)
Abstract An underwater mining navigation method based on an improved particle filter (PF) is proposed to solve the problems of non-Gaussian and intense measurement noise during underwater mining, and a new resampling algorithm is designed, as an improvement, to eliminate the influences of particle degeneration and particle impoverishment of PF. Compared to the resampling algorithms, the proposed algorithm avoids particle impoverishment and improves estimation accuracy. Finally, the estimation accuracies of underwater mining navigation algorithms based on the improved PF and the unscented Kalman filter (UKF) are compared by combining the lake trial data and underwater mining navigation model. The results of simulation experiments manifest that the proposed method has more accurate estimation and remarkable robustness.
Keywords particle filter (PF); resampling; underwater mining navigation; particle degeneration; particle impoverishment
With the discovery of more and more mineral types on the seabed, such as manganese nodule, submarine sulfide, and polymetallic concretion, underwater mining has become a promising hot spot to meet the needs of future mineral resources. In Fig.1 we show the main structure of underwater mining system which is composed of underwater mining robot, mother ship, and ore-raising system[1-2]. For underwater mining robot moving autonomously on the seabed, the underwater navigation system is a key part of the underwater mining robot to ensure the robot mines efficiently and accurately.

Fig.1 Structure of the underwater mining system
The underwater navigation is a challenging research problem because of unavailability of global positioning system (GPS) under water[3]. Currently, most underwater vehicles are generally equipped with long baseline (LBL) acoustic positioning system and dead reckoning (DR) as an integrated navigation system. LBL/DR integrated navigation system is a modern navigation system, which combines the accuracy of the LBL and the stability of the DR[4]. Although there are many navigation algorithms of data fusion of LBL and DR, most of them can not be applied to the underwater mining navigation because underwater mining robot makes a lot of noise when it begins to mine. So LBL navigation system receives a lot of noise resulting in its accuracy declining. Furthermore, the underwater mining navigation is a strong non-linear model. To solve above problems, the underwater mining navigation algorithm of data fusion has been developed a lot. For instance, Yeu et al.[1]put forward a method of data fusion based on extending Kalman filter (EKF). It transforms non-linear model to linear model by solving Jacobian matrix. The non-linear problem of navigation system is solved to some extent[1]. Wang et al.[5]proposed a navigation system based on adaptive UKF. It transforms nonlinear model to linear model by using unscented transformation and adjusting error matrix by adaptive algorithm. However, these methods mentioned above are not qualified for strong non-Gaussian and nonlinear problems in underwater mining navigation system. So, a new navigation algorithm is needed. As we know, particle filter (PF) was introduced by Doucet et al.[6]to solve nonlinear and non-Gaussian problems. An improved PF was proposed by Carpenter et al.[7]by stratified sampling and implementing sampling importance resampling (SIR) with the method based on simulating order statistics. Although the particle degeneracy is solved by implementing SIR, a new problem of particle impoverishment is brought[8]. So, an improved PF is presented by Chen et al.[9]to deal with the problems of particle degeneration and particle impoverishment in traditional PF. Currently it is an ideal solution to particle degeneracy and particle impoverishment by introducing a better resampling algorithm. The most frequently used resampling algorithms are multinomial resampling[10-11], stratified resampling[10-12], systematic resampling[10,12], and residual resampling[10-12]. The resampling algorithms mentioned above alleviate the problem of particle degeneracy, but they also bring the new problem of particle impoverishment.
Therefore, in this study, a new resampling algorithm is proposed. It hardly brings the problem of particle impoverishment. Meanwhile, it alleviates the problem of particle degeneracy. Then a new underwater navigation algorithm which combines the improved PF and underwater mining model is introduced to improve the accuracy of underwater mining navigation.
1 Background
1.1 The navigation model of underwater mining robot
In this study, the navigation model of underwater mining robot is described as follows. The state vector is defined asX=[x,y,φ,u,v,α]T, wherex,y, andφare north position, east position, and heading angle in the navigation frame, respectively,uandvare the forward velocity and starboard velocity in the vehicle reference frame, and α is the angular velocity. A first-order kinematic model isPused here. The process model is defined as
xk=xk-1+[(vk-1+P5)cos(φk-1+P3)+
(uk-1+P4)sin(φk-1+P3)]·dt+P1,
(1)
yk=yk-1-[(vk-1+P5)sin(φk-1+P3)+
(uk-1+P4)cos(φk-1+P3)]·dt+P2,
(2)
φk=φk-1+(αk-1+P6)·dt+P3,
(3)
uk=uk-1+P4,
(4)
vk=vk-1+P5,
(5)
αk=αk-1+P6,
(6)
wherePis the process noise.
The observation vector is defined asZ=[x,y,φ,u,v,α]T, and then the observation model is defined as
Zk=Xk+Q,
(7)
whereQis the observation noise.
Here, the vertical movement is neglected due to its tininess. In this work, the underwater mining navigation algorithm is proposed based on Eqs. (1-7).
1.2 Particle filter
Particle filters are sequential Monte Carlo (MC) methods based on particle representation of probability densities[12]. As a type of powerful tool for dealing with the nonlinear and non-Gaussian problems, PF has been widely used in various fields, such as signal processing[13], target tracking[14], robotics[15], and image processing[16]. There are three phases of particle filter: generation of new particles, update of particles, and computation of particle weights.
In this section, to briefly review the generic PF and analyze the resampling algorithm, the Eqs. (1-7) are simplified as
Xk=fk-1(Xk-1,Vk-1),
(8)
Zk=hk(Xk,Wk),
(9)
whereXk∈n,Zk∈mare the state vector and the measurement vector, respectively,Vk-1∈n,Wk∈mare process noise and measurement noise, respectively,n,mare the dimensions of vectors, andfk-1,hkare linear and possibly non-linear functions.

(10)
is replaced by
(11)
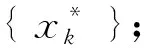
(12)
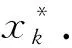
As mentioned above, four traditional resampling algorithms do not address the contradiction between improvement of estimation accuracy and maintaining the diversity of particles. In order to overcome these defects in the above resampling algorithms, a new resampling algorithm is proposed in the next section.
2 The proposal methodology
In this section, a new resampling algorithm is introduced. Then an improved particle filter is proposed based on this resampling algorithm.
2.1 A new optimal algorithm based on reinforcement learning (RL)
The proposed resampling algorithm is designed based on a new optimal algorithm. The optimal algorithm can be vividly called book-stack optimal algorithm (BOA). It is assumed there is a stack of books marked withXon the desk, and one of them is marked withxi. The book-stack can be described as
X=[x1,x2,…,xi]T,i=1,2,…,N.
(13)
It is assumed that frequency of use, which is marked withwi, is different. A set ofwican be described as
W=[w1,w2,…,wi]T,i=1,2,…,N,
(14)
(15)
Now extract a book every time according to the set ofwi. Thenwiof this book can be updated by Eq. (16).
(16)
where functionp(·) is called update function ofwi. An important property ofp(·) is described as
p(x)>x,
(17)
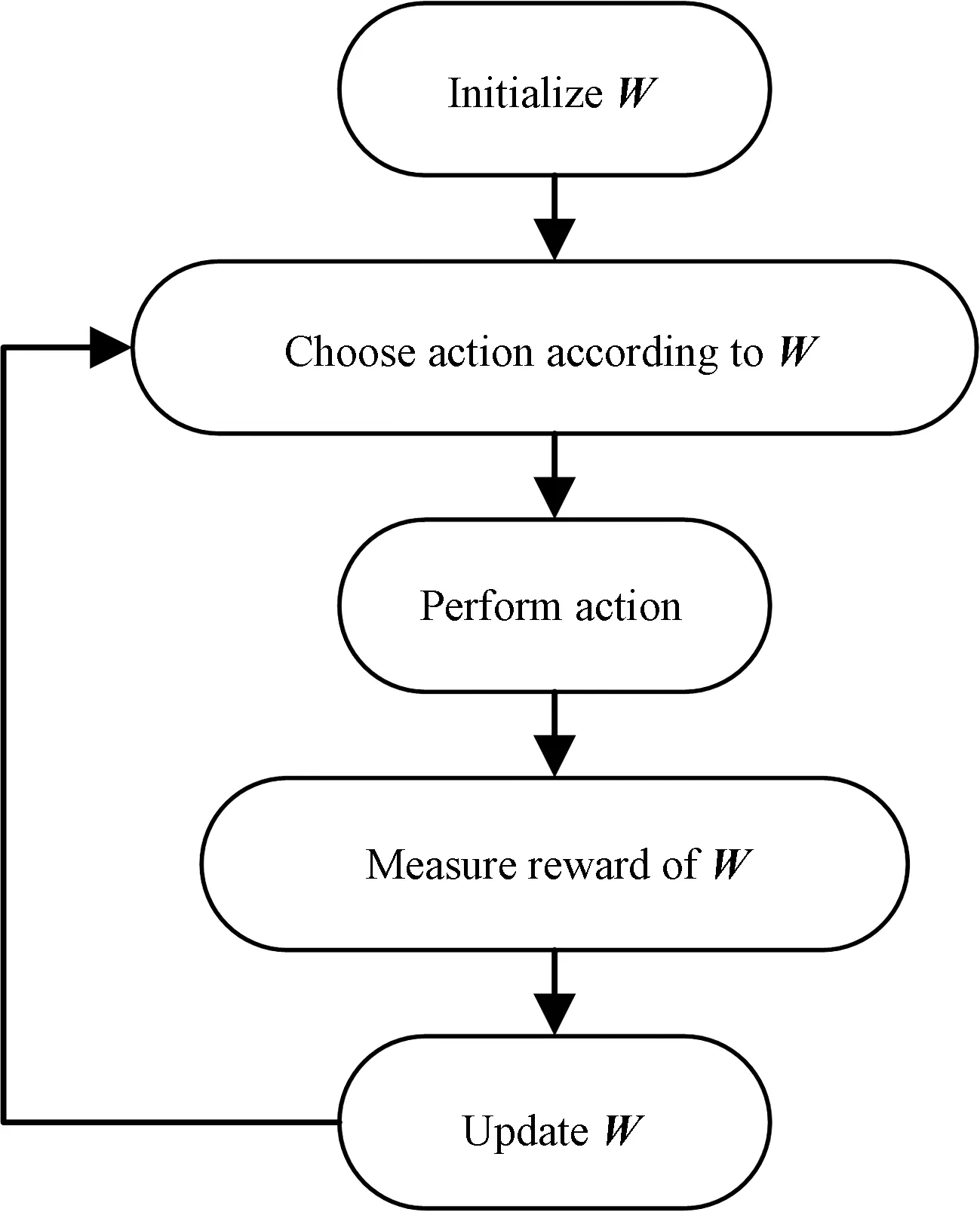
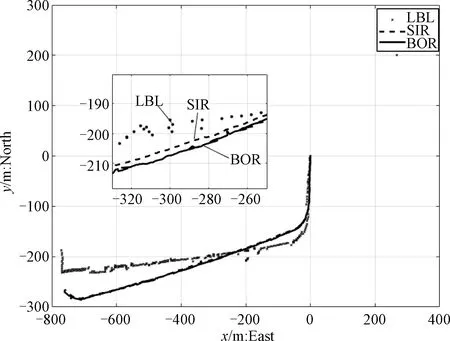
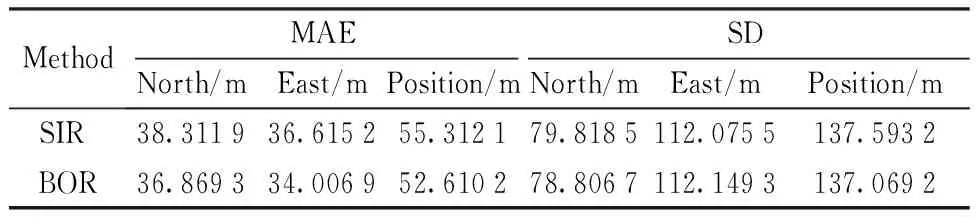
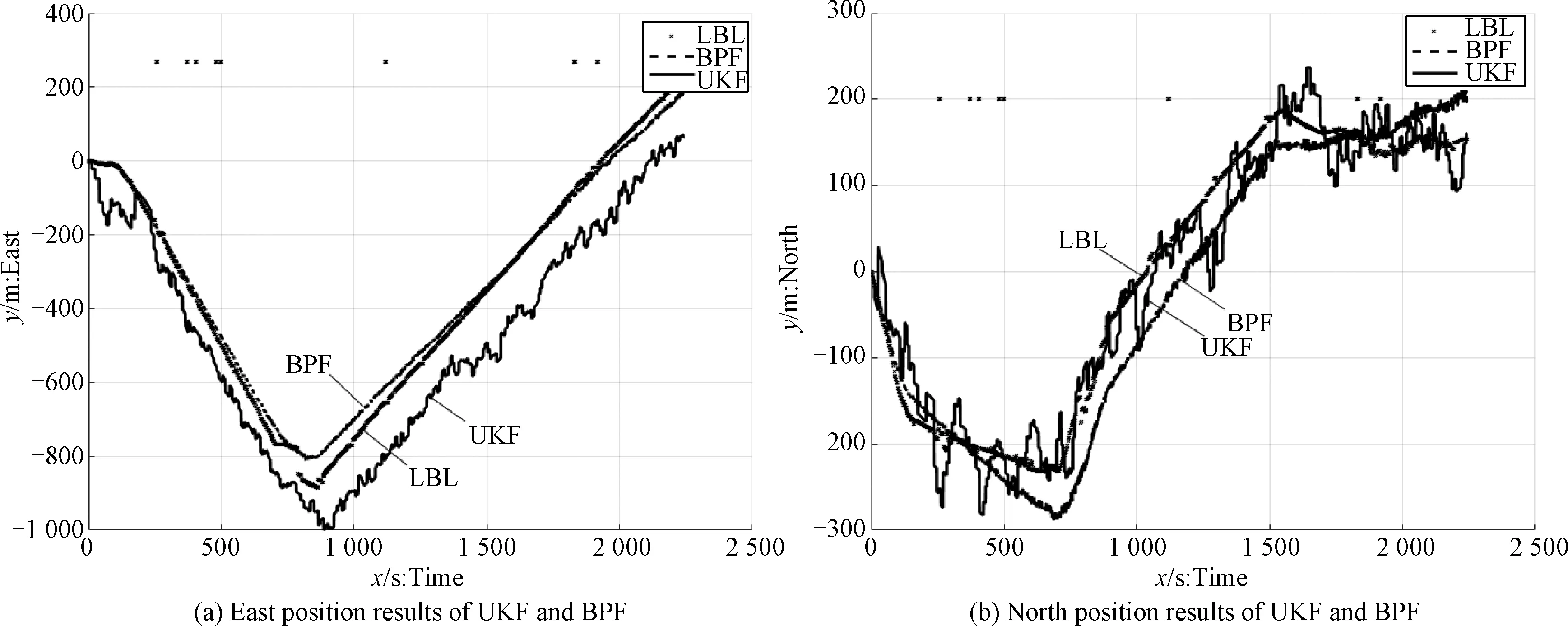
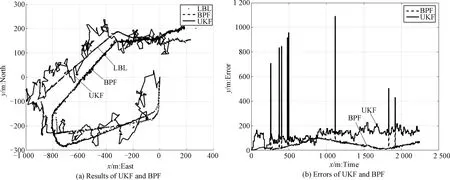
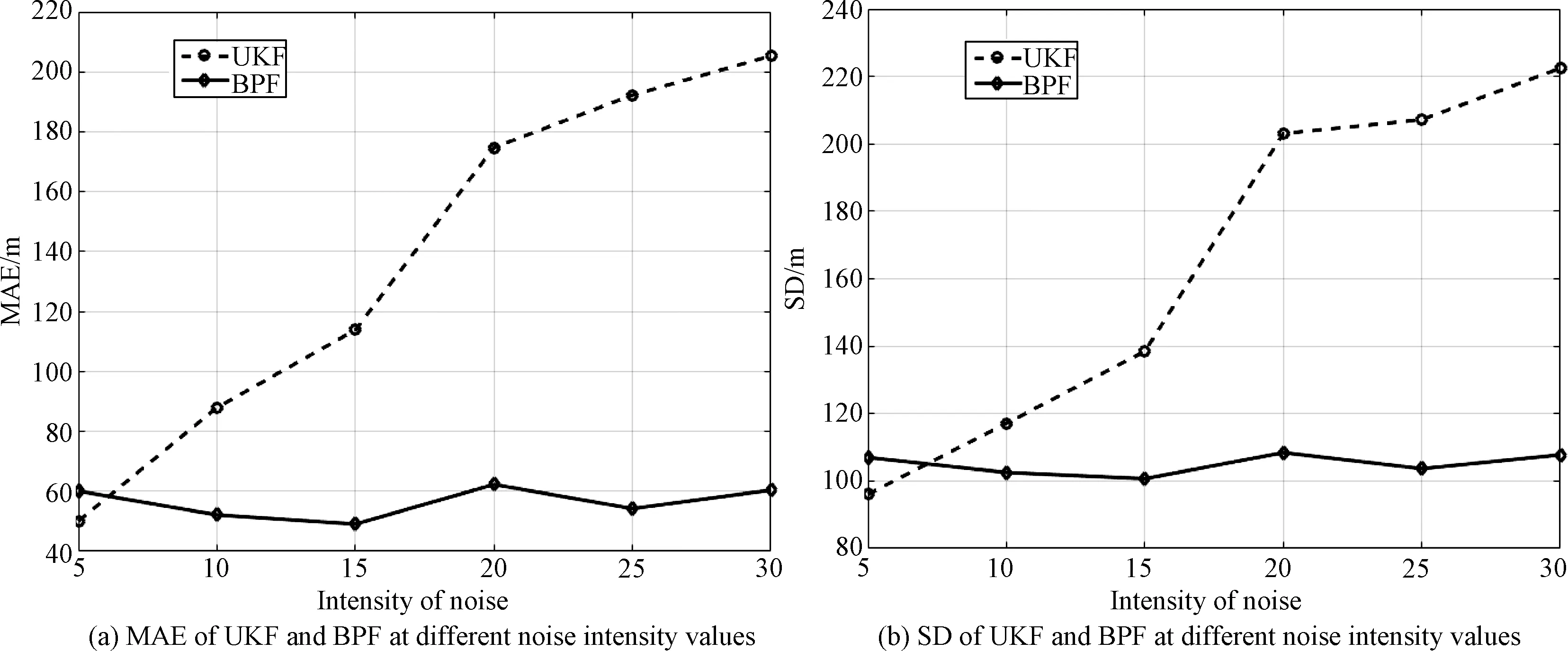
where 0 Then the book extracted is placed on the top of book-stack. After many extractions, these books whose frequencies of use are higher will be on the top of book-stack, that is to say, the book whose frequency of use is higher obtains higherwi. The process of BOA can be vividly described in Fig.2. Fig.2 The process of BOA Here, the action of RL is random sampling according to probability. The reward of RL is update ofw. The state of RL is the state ofX. So, the RL model of BOA can be described in Fig.3. Fig.3 The model of BOA based on RL Similarly, particles of PF can be considered as books in book-stack. The weight of every particle can be looked upon as frequency of use for every book. So, a new resampling algorithm is proposed based on BOA, and it is called book-stack optimal resampling (BOR). It hardly brings the problem of particle impoverishment and controls the extent of particle degeneration by adjustingp(·). Proposition2.1The resampling algorithm BOR is convergent. ProofFor simplicity, the particles of particle setX=[x1,x2,…,xn]Tare arranged in the order of the weight of normalization, i.e., in the set of weightW=[w1,w2,…,wn]T, wi>wj,i>j. (18) (19) According to Bernoulli’s law of large numbers, (20) whereniis the number of times thexiis extracted after takingNsamples. Thewiis the weight ofxi. According to the property ofp(·), i.e., p(x)>x,x∈R, (21) the order of particles in particle set is constant whenN→∞, that is to say, (22) Here,p(·) can be assumed as p(wi,i)=a·w(i), (23) (24) Further, (25) To sum up, the probability distribution function (PDF) after resampling by BOR is close to the origin PDF whenN→∞. So, the resampling algorithm BOR is convergent. An improved PF which is called BPF is designed based on BOR. The BPF includes two parts which are general PF and BOR. To introduce BPF, the model used has been defined in Eq. (8) and Eq. (9). According to the state space model used, the statistical model of the system can be defined as p(X0),p(Xk|Xk-1),p(Zk|Xk). (26) (27) (28) (29) The particle set and weights are calculated by using Eq. (27) and Eq. (28). The BOR resampling algorithm is used to deal with the particle set and weights in BPF. To describe how to apply BOR and show the main frame of BPF, the pseudocode of BPF based on MATLAB is described in Algorithm 1. In previous sections, a new resampling algorithm called BOR and an improved PF based on BOR are proposed for underwater mining navigation. To assess the performance of the proposed methods, the approaches will be tested and compared with field test data from Qiandao Lake. Qiandao Lake, a man-made lake located in Zhejiang, China, is a suitable place for underwater experiment. The lake covers an area of 573 km2and has a storage capacity of 17.8 km3. It is clear and calm. The vehicle used is a human occupied vehicle (HOV) called Shenhaiyongshi. Its features and sensors are detailed in Table 1 and Table 2. The signals of LBL, DVL, and FOG from Shenhaiyongshi are used to compose the observation vectorZkin Eq. (7). The signals of LBL are taken as north positionxand east positionyinZk. The signals of DVL are used as forward velocityuand starboard velocityvinZk. The heading angleφand angular velocityαinZkare from the signals of FOG. Table 1 Features of Shenhaiyongshi Table 2 Navigation sensors Algorithm 1 BPF algorithmInput: initial state, X0;initial weight, W0;initial covariance matrix, P; process noise covariance matrix, Q;observation noise covariance matrix, R;number of particles, N;process model, ProcessEq(·);observation model, ObservationEq(·);Output: the estimation of state, X^kFork←1to T do Fori←1to T doχi~q[Xk/(Xk-10,Zk0)],ParticleSet(i)=χi; End Fori←1to T dozi︵=ObservationEq(ParticleSet(i));Z^(i)=zi︵;Wk=Wk-1p(Xk/Xk-10)p(Zk/Xk)q[Xk/(Xk-10,Zk0)]; End Wk=Wk./sum(Wk); [Wk,ParticleSet]=BOR(Wk,N,ParticleSet); Fori←1to T doX^k=X^k+Wk(i)*ParticleSet(i); EndEndFunction ObservationEq (Xk) Zk=ObservationEq(Xk); ReturnZk;Function ProcessEq (Xk-1)Xk=ProcessEq(Xk-1); Return Xk;Function BOR (Wk,N,ParticleSet) OriginIndex=1: N, Bookcase=Xparticles; SampleIndex~sample (N, weight); %Sample according to weight, record their index. Bookcase=Xparticles; Fori To assess the performance of BOR, comparison between the PF based on BOR and the PF based on SIR is designed. The settings of the two filters should be the same: x0=[0,0,3.296 2,1.19,0]T, P0=diag{0.5,0.5,5×10-3,5×10-3,5×10-5}, P=diag{5×10-3,0.3,0.3,5×10-5}, Q=diag{5×10-3,5×10-3,5×10-3,5×10-3,5×10-5}, N=10, wherex0is the initial state,P0is the initial covariance matrix,Pis the process noise covariance matrix andQis the observation noise covariance matrix. Additionally, the update functionp(·) can be defined as p(i)=w(i)×4. (30) To simulate the mining environment of high noise, Gamma noise is added to observation signal of LBL. The gamma noise is generated by Ngamma=a×gamrnd(m,n,p,q) (31) wherea>0∈, gamrnd(·) is a MATLAB function used to return ap-by-qmatrix of gamma noise,m,nare shape parameter and scale parameter, respectively. Here,a=10. In Fig.4, it is shown that two resampling algorithms have good estimation accuracy. However, the track of BOR is closer to the track of LBL. In Fig.5 it is shown the difference of estimation accuracy between BOR and SIR. To further detail the errors of estimation, the mean absolute error (MAE) and standard deviation (SD) are introduced. They are displayed in Table 3. Fig.4 Results of the two resampling algorithms Fig.5 Errors of the two resampling algorithms It is seen in Fig.5 and Table 3 that the PF based on BOR has smaller estimation errors than that Table 3 The MAE and SD of SIR and BOR based on SIR. We analyze the positioning error data of the simulation period in Fig.5, and the PF based on SIR has more evident errors with time because the extent of particle impoverishment gradually increases. In this period, the accuracy of position rises by 4.88% according to Table 3. Therefore, BOR algorithm has more accurate estimation and alleviates particle impoverishment by changing weight of particles instead of multiplying particles. To evaluate the performance of underwater mining system based on BPF, the simulation comparing the results of UKF and BPF is designed. Similarly, the setting of two filters should be the same: x0=[0,0,3.296 2,1.19,0]T, P0=diag{0.5,0.5,5×10-3,5×10-3,5×10-5}, P=diag{5×10-3,0.3,0.3,5×10-5}, Q=diag{5×10-3,5×10-3,5×10-3,5×10-3,5×10-5}, N=100, wherex0is the initial state,P0is the initial covariance matrix,Pis the process noise covariance matrix andQis the observation noise covariance matrix. The update functionp(·) can be defined as p(i)=w(i)×4. (32) To simulate the mining environment of high noise, gamma noise is added to observation signal of LBL. The gamma noise is generated by Eq. (31). Whena=10 in Eq. (31), the fusion results and position error of UKF and BPF are shown in Figs. 6 and 7. The track of BPF is smoother than that of UKF and it is closer to the track of LBL, as shown in Figs. 6 and 7. It is seen that the BPF has more credible navigation than the UKF. Furthermore, the BPF generates an ideal track when the signal of LBL is deficient in Fig.7(a), i.e., the BPF has prominent robustness. Fig.6 Different position results of UKF and BPF Fig.7 Results and errors of UKF and BPF To reveal the advantage of BPF deeply, MAE and SD at different intensity values of noise are introduced to evaluate the estimation results of UKF and BPF, as illustrated in Fig.8. As shown in Fig.8, whena=5 in Eq. (31), the errors of UKF is smaller than those of BPF because the number of particles is little. However, the errors of UKF increase rapidly with the increase of noise intensity and the errors of BPF change little. It is seen that the BPF has the ability to eliminate the influence of noise. Fig.8 Results of UKF and BPF at different noise intensity values In this study, we have presented a new resampling algorithm called BOR as an improvement to the PF. By adjusting weight of particles instead of multiplying particles, the proposed BOR algorithm overcomes the defects of the traditional resampling algorithm and solves the problems of particle degeneracy and impoverishment simultaneously. Simulations show that the BOR algorithm improves the accuracy of estimation and maintains the diversity of particles. To address the problems of non-Gaussian and intense noise in underwater mining navigation, an improved PF based on BOR is proposed. Simulations indicate that the BPF gives very brilliant performance of estimation and the accuracy of BPF is higher than that of UKF. Further, the robustness of BPF is prominent.
2.2 A new resampling algorithm based on BOA

2.3 The improved PF
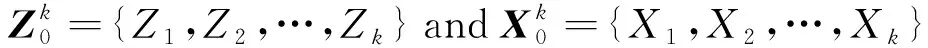

3 Application and experimental results



3.1 Comparison between BOR and SIR

3.2 Contrast between UKF and BPF
4 Conclusion

