某大型建设工程项目基于熵权及层次分析法(AHP)的投资方案研究
黄建明
(广东省广大工程顾问有限公司,广东 广州 511494)
在工程建设方案的决策过程中,决策者常常会遇到数个互有优劣的方案供选择,决策者面对此种情况常不知如何取舍、做出选择,他们即想投资利益最大化,又不愿顾此失彼,这时,若有一个能对各方案指标进行量化计算的方法提供给决策者使用,决策者就可以较轻松地对工程方案进行科学决策,从而实现工程方案决策的科学化、理性化,这样的决策过程是较为可靠的。
本文通过介绍某一特定工程项目的具体决策过程,展示一种客观性强的基于熵权法确权和主观性强的基于AHP 法确权相结合的方法,使工程方案决策者在遇到类似问题时可以不受困扰、从容决策,并进一步使工程项目建设可以较顺利地实施。
1 项目概况
某位于广州市CBD 大型商业综合体项目有4 个备选方案供选择,业主方需要考虑的投资方案要素有投资额、项目财务指标、项目社会经济效益、环境指标和安全指标等5项。业主方的投资方案决策采用的方法是熵权法和层次分析法相结合的方法,即请相关专家对4 个备选方案的5 项指标中的除投资额之外的4 项指标分别进行打分,投资额则通过相应办法处理,然后通过熵权计算以及层次分析计算得出各指标的权重,最后再通过计算综合得分确定最优方案。4 方案4 指标的得分情况及各方案投资额如下表所示:

表1
2 权重计算过程
2.1 熵权计算过程
1) 将表1 的数据构造成一个数据矩阵

其中Xij为第i个方案第j个指标的数值,n=4,m=5。2) 数据的非负数化处理
由于熵值法计算采用的是各个方案某一指标占同一指标值总和的比值,因此不存在量纲的影响,不需要进行标准化处理,若数据中有负数,就需要对数据进行非负化处理。此外,为了避免求熵值时对数的无意义,需要进行数据平移:
对于越大越好的指标:

对于越小越好的指标:
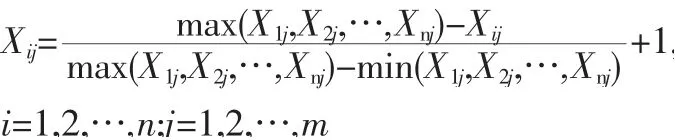
为了方便起见,仍记非负化处理后的数据为Xij。
表1 的数据经上述过程处理后得到下列表格数据:
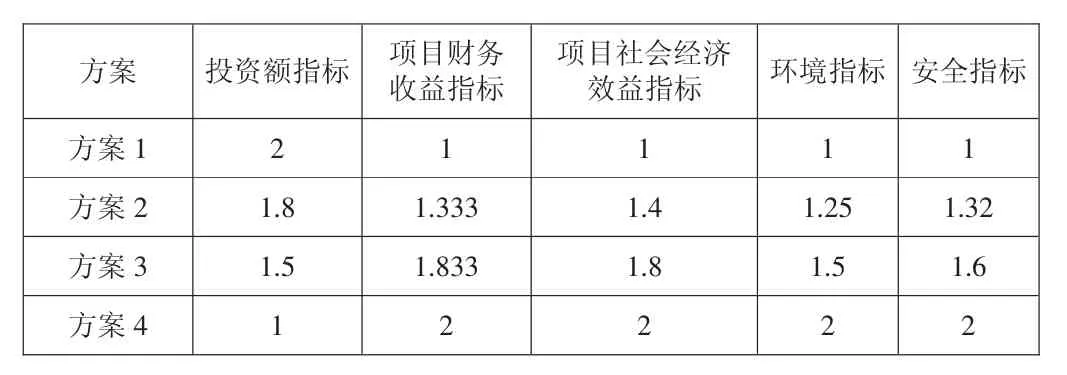
表2
3) 计算第j 项指标下第i 个方案占该指标的比重


表3
4) 计算第j项指标下的熵值

5) 计算第j项指标下的差异系数

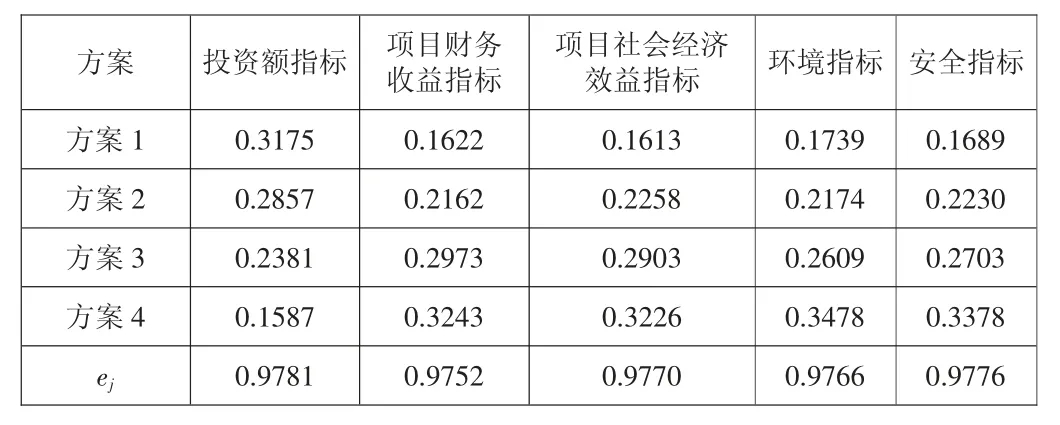
表4
6) 计算第项指标下的权数
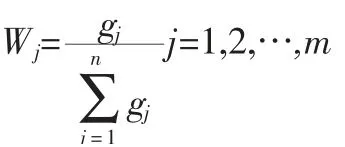
得W1=0.1896;W2=0.2147;W3=0.1991;W4=0.2026;W5=0.1939
2.2 层次分析法计算过程
1) 构造适合本工程的判断矩阵
由于本工程方案决策以一级指标的研究为主,不对二级指标做深入的研究,故本工程的层次分析研究只构造一级判断矩阵,建立两两比较的判断矩阵。具体情况如下表所示:

其中n 和m 都与投资方案需要考虑的要素相等,即等于5。
使用数值及其倒数共17 个数作为标度来确定的值,习惯上称为9 标度法。相对重要性取值如表5 所示。

表5 标度法的相对重要性取值表
对于任意的判断矩阵A,有下列性质:

根据有关专家的评分,本工程各要素的重要性两两比较的结果如下表所示:
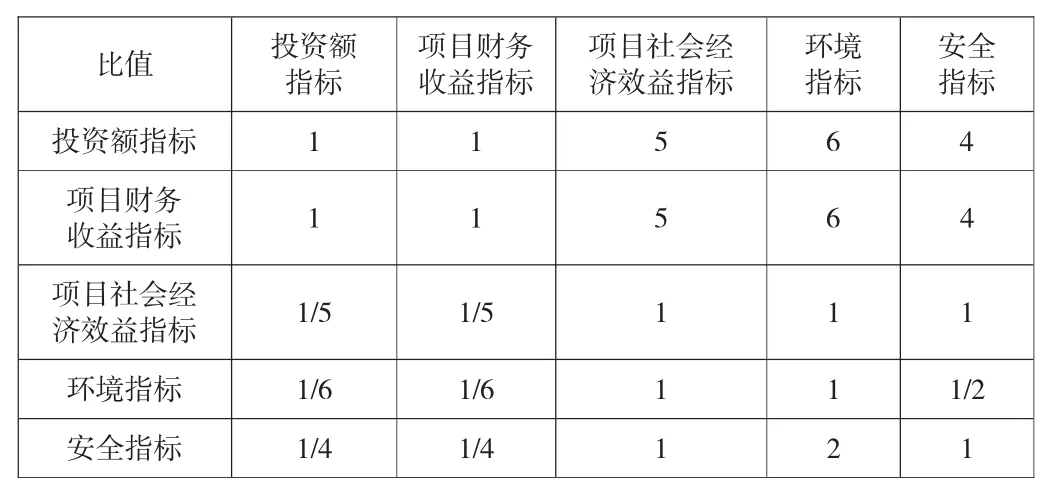
表6
2) 采用方根法计算矩阵各分量的权重
方根法是将判断矩阵A 的各行向量采用几何平均,然后归一化,得到排序权重向量,计算步骤如下:
①计算判断矩阵各行元素的乘积。
计算公式为:
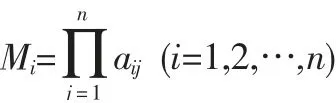
②计算乘积的n 次方根。
计算公式为:

③对向量W=(W1,W2,…,Wn) 作归一化处理。
计算公式为:

④最终得到的n 个指标的权重向量为:
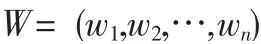
计算结果如下表所示:

表7
3) 矩阵的一致性检验
(1) 计算判断矩阵A 的最大特征值。
计算公式为:


表8
(2) 一致性检验C.I.(Consistency Index)
在决定判断矩阵系数时,要求专家两两对比的评分之间存在一致性,一致性指标的计算公式为先计算一致性指标C.I。

然后查平均随机一致性指标,当n 为5 时,查的R.I.=1.12。
最后计算一致性比例 C.R.(Consistency Ratio)。
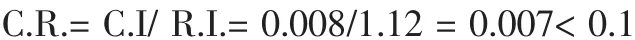
故符合一致性检验要求。
3 项目决策过程
1) 分别取各项指标的熵权数与AHP 权数的算术平均值,计算各项指标的最终权重,得:

同理,w2=0.2984 w3=0.1381 w4=0.1323 w5=0.1454
2) 根据专家的意见将表1 中的投资额转换为投标得分,得下表:

表9
3) 将各方案的各指标得分乘以各指标的最终权重,然后再求和得各方案的最终得分:
4) 确定最优方案
由于方案4 的最终得分最高,故方案4 为最优方案,该工程的决策者应采用方案4。
4 结语
在工程方案的选择决策中,采用客观性强的熵权法确权与主观性强的AHP 法确权相结合的方式确定工程决策方案各指标的最终权重并最终计算出各方案的最终得分,从而优选出优胜方案,即尊重了客观事实又尊重了专家意见,是较为科学的,也是可行的,在工程实际操作中值得同行们借鉴、研究和应用。

