一种牵引供电系统高次谐波滤除的新方法

张 路

(中国铁路兰州局集团有限公司， 兰州 730030)

随着铁路运行速度的提高，牵引供电方式发生了改变，交-直型电力机车逐步被交-直-交型电力机车取代，但同时也带来了一些问题。相较于交-直型供电方式，在谐波方面，交-直-交型供电方式3、5、7等低次谐波的含量明显减少，同时高次谐波含量增加，尤其是15次及以上谐波的含量[1]。

高次谐波的危害主要体现在以下方面：

(1) 当牵引供电系统中的自然频率叠加到频率较高的谐波电流上时，会产生共振现象。

(2) 牵引供电系统的电压总谐波发生畸变的概率会随谐振现象的发生而提高。

(3)会引起变压器绝缘老化、电容器爆浆等设备问题。

(4) 机车受到谐波谐振影响后，会发生互感器损坏，进而影响到列控车载设备，直接危及行车安全。

由高次谐波导致的牵引供电系统事故时有发生。2009年，安集变电所供电区段，运行中的CRH2动车组引发了若干次变电所牵引变压器低压侧过电压保护动作，导致上、下行接触网停电事故。2011年，沈阳局管内的沈山铁路大虎山、双羊店等牵引变电所多次发生电容器熔丝熔断事故[2]。上述事故均由高次谐波引起，造成了一定的经济损失，且危及行车安全。因此，抑制电气化铁路高次谐波对牵引供电系统的影响迫在眉睫，也至关重要。

目前，针对这一问题，已经开展了大量的研究。神华号电力机车作为重载铁路运输车型之一, 采用交直交型传动系统，由于其功率大、功率因数高，使得谐波频谱更宽, 对牵引供电系统产生的潜在危害更大。文献[3]建立了牵引供电系统和神华号电力机车仿真模型, 对不同工况下神华号电力机车谐波特性进行分析。文献[4]研究了注入牵引供电系统高次谐波电流所引起的过电压情况，分析了高次谐波过电压的一般规律及影响牵引供电系统高次谐波过电压水平的主要因素，并结合高通滤波器的滤波效果, 给出了牵引供电系统高次谐波过电压抑制技术方案。文献[5]研究了牵引供电系统主要组成元件的谐振灵敏度，优化了牵引供电系统结构，使牵引供电系统谐波含有率降低。文献[6]针对高速铁路系统提出了一种可滤除高次谐波和抑制谐振的新型阻波高通滤波器，使牵引网谐振频率避开机车的高次谐波电流频率，从而抑制谐振。

谐波抑制途径有三个方面，分别为优化外部电源、优化牵引传动系统、优化地面牵引变电所。

上述方法仅对既有牵引供电系统进行优化，以减少进入牵引供电系统中高次谐波含量的方法抑制谐波。本文从可实现性方面考虑，采用在地面牵引变电所加装滤波装置的方法，抑制高次谐波对牵引供电系统的影响。

1 混沌滤波原理的深入研究

1.1 滤波原理

近年来，随着混沌学科的大力发展，其在“无用”谐波滤除方面的优势也被研究。目前，运用较多的混沌方程为[7]：

x″(t) +kx′(t)-x(t) +x3(t)=Acosωt+acosω1t

(1)

式中：k——系统阻尼比；

x(t)+x3(t)——非线性控制项；

A——杜芬系统内策动力幅值；

ω——杜芬系统内策动力角频率；

a——外策动力幅值；

ω1——外策动力角频率。

当内策动力频率ω固定，随着加入系统外策动力项频率ω1的不同，系统会出现混沌态及大尺度周期态[8]。

利用混沌理论滤除高次谐波的原理是，将系统内策动力项频率设为基波对应的频率，外策动力项加入到系统后，若系统的响应为混沌态，则认为加入到系统中的是高次谐波而将其滤除。若系统的响应为大尺度周期态，则认为加入系统中的是基波而不被滤除。

已有的研究中，通常利用从混沌态到大尺度周期态的转变作为系统发生响应的判定。本文提出逆相变判别法，将大尺度周期态认为混沌系统的常态，即外策动力频率与内策动力频率相同时系统处于的状态。一旦加入系统的外策动力频率与内策动力频率不同，则系统发生了由大周期态向混沌态的逆向响应。反应在高次谐波滤除上，当没有高次谐波存在时，进入到滤波系统的是与内策动力频率相同的基波信号，此时系统处于大尺度周期态，一旦进入系统的是与内策动力频率不同的高次谐波，系统的输出响应为混沌态，即产生了由大尺度周期态到混沌态的逆跳变，说明滤波系统识别出高次谐波并将其滤除。

为验证滤波系统的灵敏度，即系统到底能够对与基波频率相差多大的谐波作出反应，本文做了如下研究，在参数设置环节，首先将系统内策动力频率设为基波50 Hz对应的频率，调整内策动力幅值，接着在外策动力项中加入牵引电流3次谐波，得到的结果如图1(a)所示，可以看出系统仍然处于混沌的状态，未对加入的牵引电流3次谐波作出响应。接着保持内策动力项各项参数不变，在外策动力项加入牵引电流50 Hz基波，得到结果如图1(b)所示，可以看出在内策动力参数一定的情况下，50 Hz基波能够使系统作出相应。而与基波频率接近的3次谐波不能够使系统处于大尺度周期态，进而将与基波频率相同的牵引电流3次谐波滤除。

图1 系统响应灵敏度测试图

1.2 存在问题及算法改进

本文在进行了大量仿真实验后发现，参数设置仍将 50 Hz基波频率作为系统内策动力频率，当系统接收到的外策动力为不同次的高次谐波时，系统始终处于混沌态。当外策动力为与基波接近的高次谐波时，若其存在一定的初相角，也会使系统发生改变，使系统误认为是50 Hz的基波频率而不把其滤除，从而产生误判。

外策动力项存在初相角情况下其混沌方程为：

x″+kωx′-ω2(x-x3)=ω2[Adcosωt+

acos((ω+Δω)t+φ)]

(2)

式中：Δω——外策动力项与内策动力项之间的频差；

φ——外策动力项初相角；

Ad——系统临界阈值。

为验证上述情况，进行了如下试验。在参数设置环节，首先将内策动力频率ω取50 Hz，然后在系统中加入7次谐波，其初相角φ=2π/3，即加入到系统中的牵引电流7次谐波存在一定的初相角，得到结果如图2所示。

图2 加入含有相角的七次谐波系统输出相图

由图2可知，系统处于大周期态。若加入系统的是与基波不同的牵引电流7次谐波，则系统响应应是抑制排斥的混沌态，而不应是接受通过的大周期态，但本次试验得到的结果恰恰相反，虽然加入系统外策动力项的是牵引电流7次谐波，但由于其含有初相角，系统也错误地做出了大尺度周期态响应，说明既有的研究存在纰漏，需进一步研究。

为了解决上述问题，对既有模型进行了深入研究，提出内策动力相角“移位”法，使其由0变为π，改进步骤如下：

(1)调整系统初始参数，主要对内策动力项的各参数进行设定，等待外策动力项的输入。如混沌滤波系统接收到的外策动力项不会使系统发生改变，即处于混沌抑制态，则输入到系统的外策动力项被当作高次谐波被滤除；若滤波系统接收到的外策动力项使系统发生改变，即处于大周期接收态，则说明进入滤波系统的外策动力可能是50 Hz的牵引电流基波，也有可能是带有初相角的与基波频率接近的高次谐波，需进行下一步骤。

(2)对于使系统处于大尺度周期接收态的外策动力项，系统内策动力项根据设定，运用“移位”法使内策动力相角偏移，再次观察系统的输出状态。若此时系统由大尺度周期接收恢复到混沌抑制态，说明进入系统的是带有初相角的高次谐波，系统表现出“排斥”状态将其滤除；若系统仍然处于大周期接收态，则表明此时外策动力项是与内策动力频率相同的牵引电流基波。

综上，系统只“接收”与内策动力频率相同的牵引电流基波，对于与基波频率不同的牵引电流高次谐波，混沌滤波系统不会做出响应，将其作为噪声滤除。从而实现了对牵引供电系统高次谐波的完全滤除。

2 牵引供电系统谐波抑制仿真验证

2.1 搭建仿真模型

为消除牵引供电系统中高次谐波的危害，根据混沌方程搭建仿真模型，如图3所示。

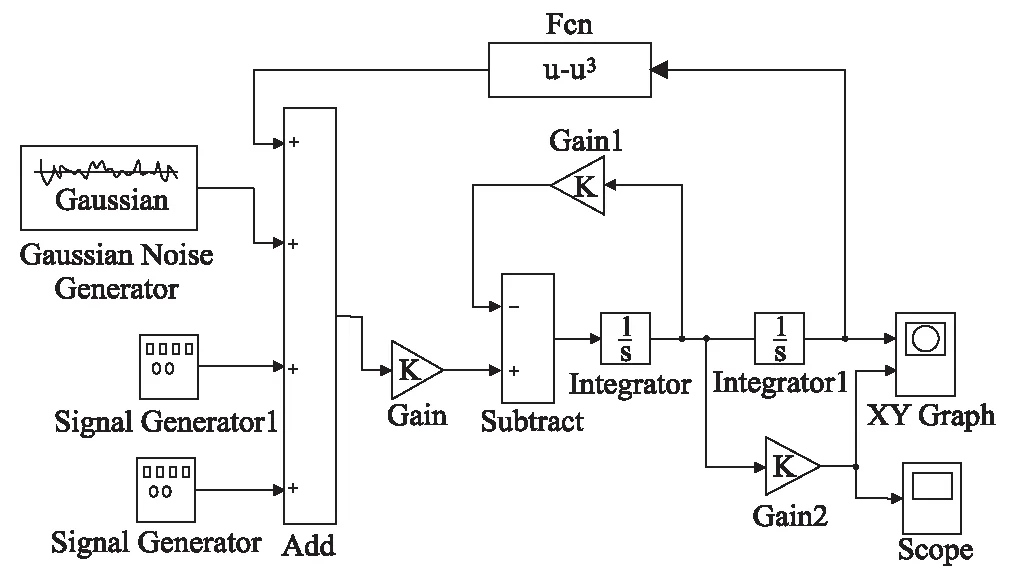
图3 仿真模型图

其中，Signal generator块为系统的内策动力项，Signal generator1块为系统的外策动力项，系统中专门加入的Gaussian Noise Generator块可消除除了牵引电流高次谐波外的其他可能会对牵引供电系统产生危害的因素，Fcn块是函数项，Cain和Cain1为系统的增益模块，Add为系统的加法器模块，Subtract为系统减法器模块，Integrator和Integrator1为系统积分模块，XY Graph和Scope为系统的输出模块。

2.2 仿真验证

仿真模型搭建完成后，根据改进步骤进行仿真验证。

(1)对内策动力项的各参数进行设定，将Signal generator块中的频率设为50 Hz的牵引电流基波频率，在Signal generator1块中加入9次谐波，并将其初相角设为φ=2π/3，得到仿真结果如图4所示(图中曲线粗糙，是由Gaussian Noise Generator块产生的噪声所致)。可以看到系统处于大尺度周期接收态，此时不能盲目认定输入系统的就是50 Hz牵引电流基波。进入系统的可能是50 Hz的牵引电流基波，也有可能是带有初相角的与基波频率接近的高次谐波。

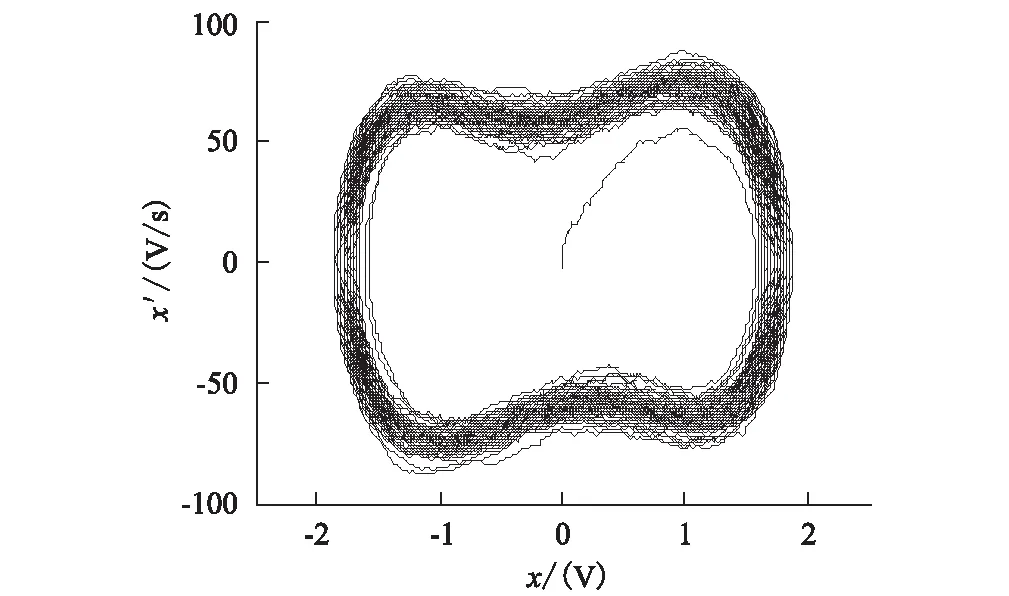
图4 加入9次谐波系统输出相图

(2)进一步进行试验，依然将Signal generator块中的内策频率设为50 Hz的牵引电流基波频率，在Signal generator1块中加入11次谐波，将外策动力初相角设为φ=2π/3，得到仿真结果如下图5(a)所示。可以看到带有相角的11次谐波使滤波系统处于大周期接收态。此时，在Signal generator块中将内策动力相角设为π，即进行了“移位”，得到结果如图5(b)所示。可以看到内策动力项相角“移位”后，滤波系统识别出牵引电流11次谐波，系统仍然处于混沌抑制态。

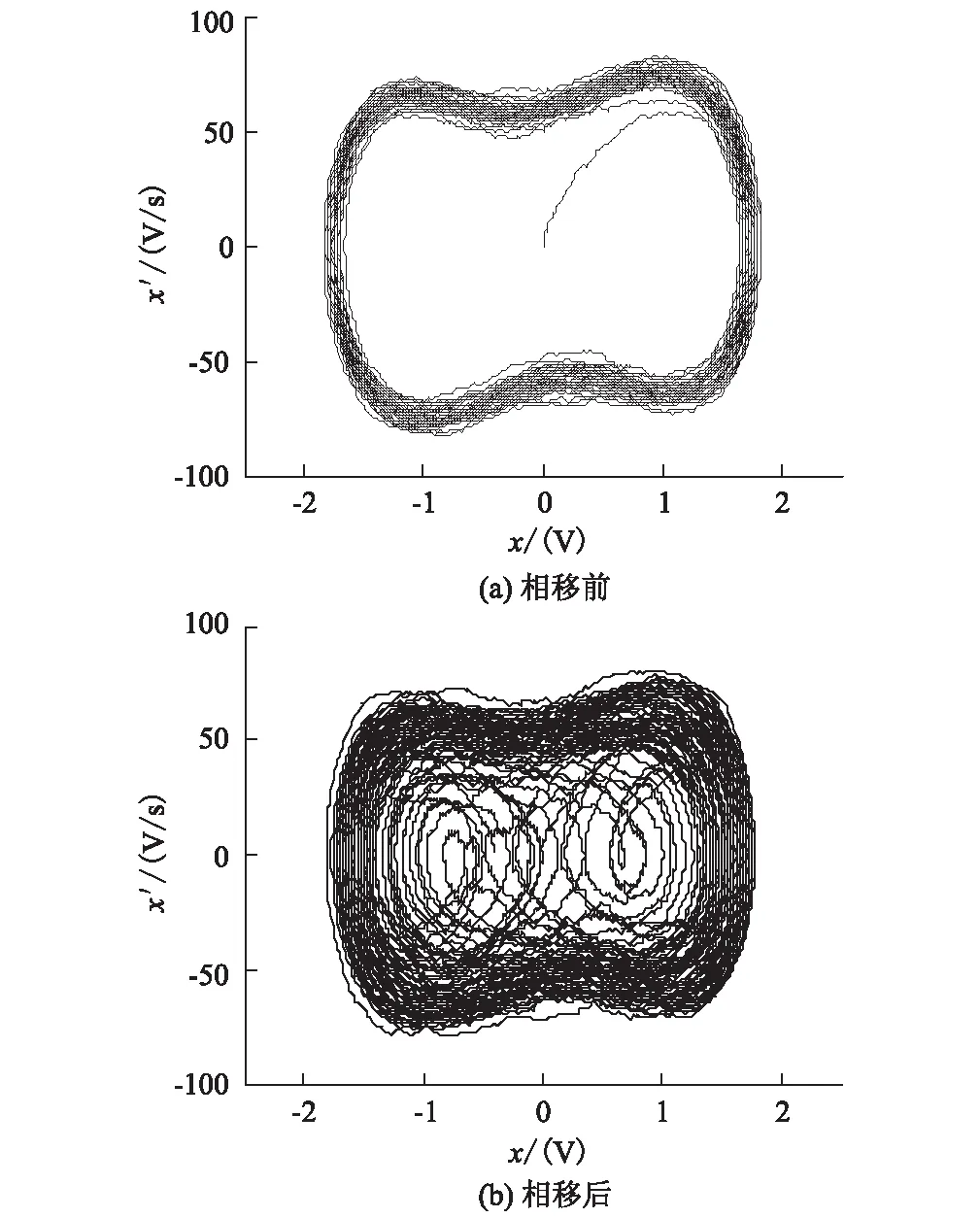
图5 改进后系统输出相图

经过上述仿真研究发现，仿真验证结果与理论研究一致，为消除由于牵引电流高次谐波带有初相角而导致的系统漏滤，从混沌模型源头上提出改进，对算法进一步的完善，可以看到混沌系统可对牵引供电系统中的高次谐波进行有效抑制。今后可在地面牵引变电所加装混沌滤波装置抑制高次谐波，避免对牵引供电系统的影响，保证牵引供电系统的安全运作。

3 结论

本文从高次谐波对牵引供电系统产生的危害入手，运用混沌理论在谐波抑制方面的优势，改进既有模型的不足，搭建仿真模型分别验证了9次谐波及11次谐波加入系统后的情况，结果表明改进后的系统可对牵引供电系统中的高次谐波进行有效抑制，并可消除高次谐波带有初相角时的系统纰漏。文章在铁路牵引供电系统谐波抑制方面提出了一种新的思路，下一步

将进一步应研究如何将此系统运用于现场实际，为铁路牵引供电系统谐波抑制做出贡献。