计及ψ-i 型JA磁滞电感的变压器铁芯仿真建模及验证

邹 密

（重庆邮电大学自动化学院，重庆400065）

0 引 言

变压器是电力系统中最关键的设备之一，其电磁暂态建模时，从变压器组成结构上看，通常需要计及变压器绕组和铁芯两部分［1-3］。变压器绕组对应为变压器电路结构，通常为线性模型，可用一定结构的电阻和电感等值电路模拟［4-6］；变压器铁芯为变压器磁路结构，铁芯通常由铁磁材料制造而成，铁芯在变压器运行过程中将传导主磁通，具有非线性磁滞特性［7-9］。

铁芯非线性磁滞特性及动态损耗特性是影响变压器低频电磁暂态过程非常关键的因素，变压器铁芯模型的精确程度直接影响着整个电力系统电磁暂态仿真结果的精确性［10-11］。现有变压器低频电磁暂态模型研究中，常采用单值磁化曲线来模拟变压器铁芯的非线性特性，该处理方法能够在一定程度上体现铁芯的非线性特性［12］。变压器的非线性特性不仅包含饱和特性，还包含磁滞效应，采用单值初始磁化曲线会造成电磁暂态分析结果误差偏大，降低整个系统的电磁暂态仿真结果的可信度［13］。在动态损耗表征方面，铁芯损耗将直接影响铁磁谐振等低频电磁暂态过程中电磁能量的转换，若仅考虑铁芯静态磁滞损耗特性，忽略涡流损耗以及额外损耗，将会造成较大的稳态及暂态过电压、过电流分析误差［14-15］。

现有磁滞模型通常以磁感应强度B和磁场强度H为输入和输出，该类B-H型磁滞模型主要面向于磁性材料特性的应用，难以在以电压和电流为基准的电磁暂态仿真（Electromagnetic Transient Program-Alternative Transients Program，EMTP-ATP）类软件中采用软件底层模块或语言实现［16-17］。由于现有研究方法在处理变压器磁滞特性和动态损耗特性等方面的不足，建立更准确的变压器铁芯仿真模型仍然是本领域的研究难点和重点。

以传统B-H型Jiles-Atherton（JA）磁滞方程为基础，结合电磁暂态仿真中JA 磁滞模型微分方程表达式，提出ψ-i型JA 磁滞模型，并基于磁感应强度与电压以及磁场强度与电流之间关系，推导建立电压驱动型动态ψ-iJA磁滞电感模型，研究在EMTP-ATP 中采用Type-94 元件以及Model language 实现上述磁滞电感的流程和步骤，并以单相铁磁谐振试验结果为依据，验证变压器铁芯仿真模型的正确性。

1 变压器铁芯模型

1.1 经典JA磁滞模型

经典JA 磁滞模型是由Jiles 和Atherton 两位学者［18］在1984 年提出，并通过试验进行验证，其基本思想是磁化过程中磁畴和磁畴壁的弯曲和平移。由能量平衡方程可得静态JA磁滞模型：

式中：H为磁场强度；M为磁化强度；Ms为饱和磁化强度；a为无磁滞磁化曲线形状参数；c为磁化因数，可以通过试验测得；α 为平均场参数，反映磁畴间的耦合；μ0为真空磁导率；k为牵制系数；δ 为方向系数，当dH/dt≥0 时，δ ＝1；当dH/dt＜0，δ ＝ -1。

1.2 ψ-i型JA磁滞模型

由安培环路定律可知，磁感应强度B与磁链ψ为线性关系，磁场强度H与电流i存在线性关系，定义连续性方程：

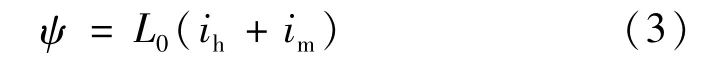
式中：ih为磁场强度电流，im为磁化强度电流，L0为饱和电感，其值与真空磁导率、面积以及绕组匝数等相关。

在经典JA 磁滞模型中，将式中dMan/dH用代替，并将Man、Ms、He、M、H分别用相应电流分量iman、imsat、ieff、im、ih替换，可得到如下ψ-i型JA模型：

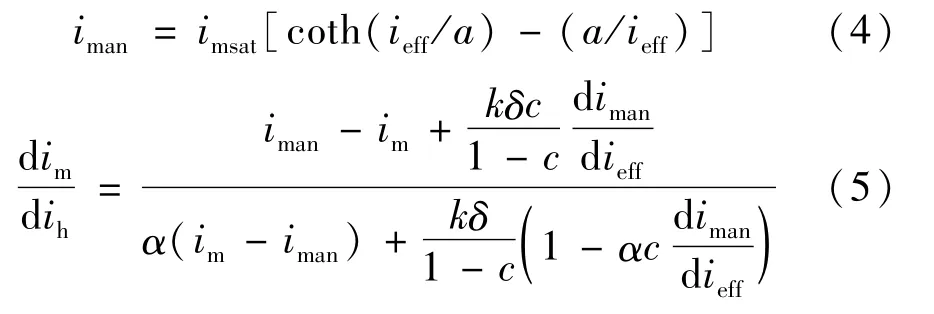
式中：ieff为有效电流；ieff＝ih+ αim；iman为无磁滞磁化电流；imsat为饱和磁化电流；δ 为电流方向参数，当dih/dt＞0 时，δ ＝1；当dih/dt≤0 时，δ ＝ -1；其余参数与式（2）中对应参数具有相同物理意义。

1.3 JA磁滞电感的实现

在EMTP-ATP中实现ψ-i型JA磁滞电感，其元件连接如图1（a）所示。

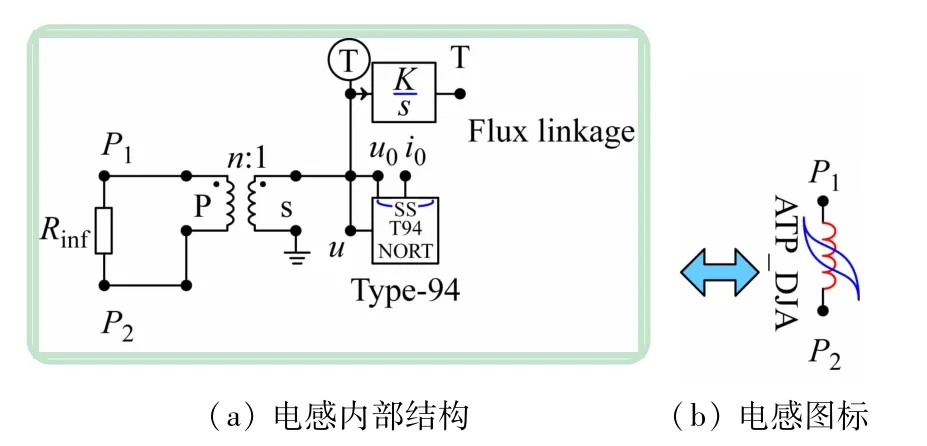
图1 ψ-i型JA磁滞电感

具体计算步骤：

步骤1设当前EMTP-ATP 计算时间为t，Norton电流源前一时刻参数g［t-Δ（t）］和I［t-Δ（t）］以及当前时刻输入电压u（t）已知；

步骤2通过EMTP-ATP 中HISTORY 语句可以保存上一时刻参数u［t- Δ（t）］，ψ［t- Δ（t）］，ih［t-Δ（t）］，im［t-Δ（t）］，iman［t- Δ（t）］以及ieff［t-Δ（t）］；

步骤3采用Integral 语句可以计算此时的磁链ψ（t）以及磁链增量Δψ，定义磁滞电流变化量最大值为Δihmax＝ Δψ/L0，并据此计算此时ih（t）和im（t），Q为静态磁滞电流比例系数，其取值范围为［0，1］）；

步骤4计算有效电流ieff（t）＝ih（t）+αim（t），并据式（4）计算无磁滞磁化电流iman（t）；

步骤5判断（iman-im）δ 正负，并据式（5）计算dim/dih；通过计算得到的dim/dih修正Q，直到Q满足要求为止，则完成t时刻的JA微分方程求解。在整个循环计算过程中Q为一个变化的系数不断更新，直至每次计算出的dim/dih满足要求为止，Q的初始值设置为0.5。

在Type-94 元件前串联变比为1∶1的单相理想变压器，其目的在于Type-94 元件在EMTP-ATP 中默认为内部接地，串联理想变压器后，可将默认接地的Type-94 元件转换为不接地，便于该磁滞电感用于变压器铁芯各磁支路建模，在理想变压器入口接有阻值为10 MΩ的电阻Rinf，主要用于保持仿真时数值稳定性，在Type-94 元件上方接有TACS积分元件，可将电压积分值直接输出。将图1（a）在ATPDraw 采用compress命令压缩后，对其输入、输出接口以及图标进行编辑，可得如图1（b）所示的等效电感。

2 铁磁谐振仿真模型

基于上述动态ψ-iJA磁滞电感，在EMTP-ATP 中建立单相铁磁谐振仿真电路如图2 所示，其中u为系统电源，Cs为串联电容，Cg为对地并联电容，ATP＿DJA为模拟变压器的磁滞电感。文献［19］中指出，铁磁谐振更容易发生在变压器或PT 空载或者轻载时，系统串联阻抗相对于容抗而言很小，可忽略串联阻抗。由于铁磁谐振对系统初始条件非常敏感，仿真与试验采用相同初始条件，即电容残压和变压器剩磁均为零，仿真步长为1 μs。

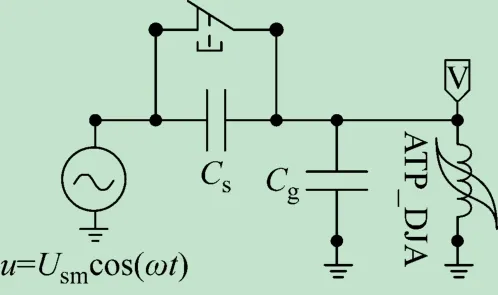
图2 EMTP-ATP中单相铁磁谐振仿真电路

3 实验结果及验证

以上述铁磁谐振仿真电路为基准，采用低压自制饱和试验变压器开展铁磁谐振试验研究，变压器容量为360 VA，电压变比为1∶1。图3 所示为单相铁磁谐振试验图，其中电流测量为Tektronix A622 探头，电压波形由Tektronix TDS 1002 示波器存储。

图3 铁磁谐振试验

当系统参数分别为Us＝40 V；f＝50 Hz；Cs＝253 μF；Cg＝42 μF 时。在t0＝100 ms开关打开，图4 为此时系统电感电压时域波形图。从图中可以看出，经过约90 ms的暂态过程后，试验变压器一次侧电压进入稳定基频铁磁谐振状态。试验所得稳态电压峰值为36.71 V，而仿真所得稳态电压峰值为37.38 V，稳态谐振峰值电压误差为1.83%，与此时电源电压相比，试验与仿真稳态电压峰值倍数分别为0. 92 p. u.和0.93 p.u.，即此时稳态谐振电压相对于电源电压略微下降。

图4 基频铁磁谐振电压波形图

单相分频试验与基频试验激发铁磁谐振的方式不同，通过多次反复试验发现，分频谐振在开关打开，并联电容已经并联好的情况下，直接将开关投入电源才能激发。因此，仿真过程中也是通过投入开关进行激发。当系统参数分别为Us＝ 20 V，Cs＝700 μF，Cg＝20.36 μF 时，在t0＝0 投入电源，图5 为此时电感电压时域波形图，经过约80 ms的暂态过程后，电压进入稳定分频谐振状态（仍含有一定50 Hz分量）。试验所得稳态电压峰值为26.19 V，而仿真所得稳态电压峰值为27.48 V，稳态谐振峰值电压误差为4.93%，与此时电源电压相比，试验与仿真稳态电压峰值倍数分别为1.31 p.u.和1.37 p.u.，即此时稳态谐振电压相对于电源电压升高。

图5 分频铁磁谐振电压波形图

4 结 语

提出了一种电压驱动型动态ψ-iJA 磁滞电感模型，该电感模型以电压和电流作为输入和输出，不再依赖于B-H磁滞回线求取模型参数，该方法为基于动态JA磁滞模型的变压器低频电磁暂态模型的工程应用奠定了基础。

铁磁谐振试验和仿真结果表明，所建立的变压器低频电磁暂态模型能够以较高精度用于电磁暂态仿真，稳态谐振峰值电压误差为1.83%和4.93%。