基于混合蛙跳算法的研究
葛 鹏,李冬林,杨俊胜,方栋泽,代永强
(甘肃农业大学信息科学技术学院计算机科学与技术专业,甘肃 兰州 730070)
0 引言
混合蛙跳算法是由Eusuff和Lansey为解决组合优化问题于2003年首次提出的,目的就是为了找出最优组合[1],混合蛙跳算法的特点为概念简单明了,需要调整的参数少,鲁棒性强,解决问题时计算速度快,寻找最优解的能力比普通算法强以及最为重要的易于实现的特点。
混合蛙跳算法的背景是在一片沼泽地里青蛙利用沼泽地中离散分布的石块去寻找更多食物,每只青蛙个体之间都进行信息的交流[2],通过整个种群的信息交流,来使每只青蛙得到最多的食物。转换为算法的思想,即为使得每个解都达到最优,最终使整个算法达到最优解,即由局部最优到全局最优的过程。蛙跳算法对于解决算法当中的n后问题和最短路径问题等有显著效果。
1 混合蛙跳算法的实现过程
Step0:对每一个个体初始化,确定试验次数,混合迭代次数,个体总数,族群数,个体维数,族群内更新次数的值,并调用测试函数对初始化所产生的解进行优化。
Step1:以 main函数进入算法,按照适应度降序对全部个体进行排序和族群划分[3],同时对解进行排序、分组为M,每个组内有I个个体。
Step2:对某个群组中的个体进行重新排序,对排序分组的族群进行局部更新寻找局部最优pb,局部最差pw[4]。
Step3:重复Step2,直至所有族群均被更新。
Step4:从局部最优中寻找全局最优并将值赋给px,将 pop[M][I](排序后的族群)复制到 individual。
Step5:对结果求平均极值及标准差,输出标准差及平均值极值,得到最终的实验结果。
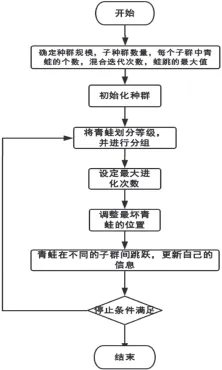
图1 混合蛙跳算法流程图Fig.1 Mixed frog jump algorithm flowchart
2 测试函数

表1 测试函数Tab.1 Test functions
3 算法各参数的改变对函数的影响
3.1 族群内更新次数对各函数平均极值的影响
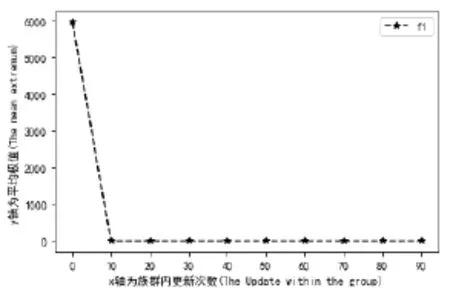
图2 族群内更新次数对平均极值的影响Fig.2 The effects of the number of updates in the population on the mean extremum

图3 族群内更新次数对平均极值的影响Fig.3 The effects of the number of updates in the population on the mean extremum

图4 族群内更新次数对平均极值的影响Fig.4 The effects of the number of updates in the population on the mean extremum
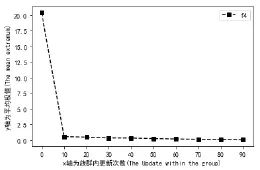
图5 族群内更新次数对平均极值的影响Fig.5 The effects of the number of updates in the population on the mean extremum
3.2 维度对各函数平均极值的影响

图6 维度对平均极值的影响Fig.6 The effect of dimensions on the mean extremum

图7 维度对平均极值的影响Fig.7 The effect of dimensions on the mean extremum

图8 维度对平均极值的影响Fig.8 The effect of dimensions on the mean extremum

图9 维度对平均极值的影响Fig.9 The effect of dimensions on the mean extremum
3.3 维度对各函数标准差的影响
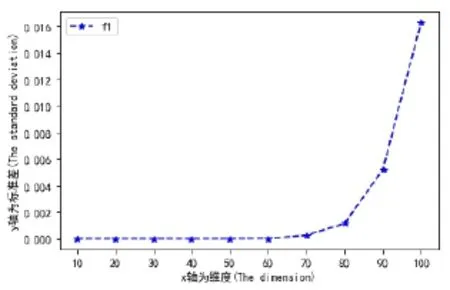
图10 维度对标准差的影响Fig.10 The effect of dimension on standard deviation

图11 维度对标准差的影响Fig.11 The effect of dimension on standard deviation

图12 维度对标准差的影响Fig.12 The effect of dimension on standard deviation
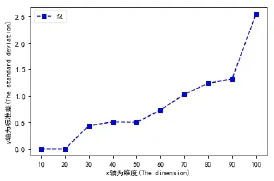
图13 维度对标准差的影响Fig.13 The effect of dimension on standard deviation
3.4 族群内更新次数对各函数标准差的影响

图14 族群内更新次数对标准差的影响Fig.14 The effect of the number of population updates on the standard deviation

图15 族群内更新次数对标准差的影响Fig.15 The effect of the number of population updates on the standard deviation

图16 族群内更新次数对标准差的影响Fig.16 The effect of the number of population updates on the standard deviation
4 结论
在保持试验次数,混合迭代次数,个体总数,族群数,族群中的个体数不变时,利用四种测试函数对算法进行研究,通过测试发现不同函数对于算法优化有着不同的效果。图2至图9中表明:当族群内更新次数增大时,f1、f3和f4函数的平均极值逐级递减,向理论最优值靠拢,算法优化效果较好。而当维度数增大时,f1、f3函数的平均极值增大,f4函数递减。从图10至图17中表明:维度增大时,f1、f3、f4三种函数的标准差均增加。族群内更新次数增大时,f1、f3函数标准呈递减趋势,f4函数总体递减但中间产生突变。但是,无论是维度增大还是族群内更新次数的增加,f2函数对算法的平均极值和标准差保持不变。本实验的不足之处在于仅仅只是研究了混合蛙跳算法两个相关参数的改变对混合蛙跳算法的影响,试验次数相对较少,后续会继续改进。
5 结束语

图17 族群内更新次数对标准差的影响Fig.17 The effect of the number of population updates on the standard deviation
数据无处不在,对于数据的处理和整合以成为现实生活中不可避免的问题,混合蛙跳算法则是在对各类数据的整合过程中寻求其对于解决问题的最好方式之一。当今世界,和平与发展是时代主旋律,面对各种资源分配不均导致地区经济发展的不平衡,以及资源的分配不均,应用普通的优化算法例如像梯度算法,Hessian矩阵,拉格朗日乘数,单纯形法[6],梯度下降法等一系列算法已经不能解决对于各类数据处理整合优化的需要。因此,需要寻找优化性能更为强大的算法。相对于普通的优化算法,混合蛙跳算法具有设置参数少,简单易于理解,鲁棒性强的特点[7],对于解决多种数据的实时变化和最优解的寻求问题有着明显的优势。

