空气预热温度对天然气加热炉内温度场和NOx排放的影响

周仲伟，郭 韵

（上海工程技术大学机械与汽车工程学院，上海 201620）

0 引言

天然气在使用过程中常常需要加热，如在天然气的开采和运输过程中需要借助加热炉将天然气加热至适宜温度，防止由于天然气温度过低而导致其中含有的水合物析出凝结成固体,进而堵住管道设备引起事故。此外，在液化天然气(LNG)输配应用系统中，要使LNG气化，也必然需要对其加热[1,2]。然而，天然气加热炉却存在很多性能缺陷，比如结构庞大、污染物排放浓度高和传热效率低等，因此对天然气加热炉进行节能优化研究显得尤为重要。很多学者对如何提高加热炉的传热效率和降低燃烧污染物排放等方面开展了大量工作。

尹洪超等[3]针对某烯烃厂芳烃加热炉在不同空气预热温度情况下的燃烧状况和 NOx排放规律做了研究，并由此得出了针对该加热炉的空气预热最佳温度。张永学等[4]用计算燃烧学的方法对某石化公司F101立式圆筒加热炉内的温度场进行了计算，实际工况温度计算结果与现场测试结果吻合良好，表明了当空气预热温度达到最佳值时，加热炉热效率最高。张琳等[5]以某石化公司的 F1001常压炉为研究对象，采用非预混湍流扩散燃烧PDF模型对不同空气预热温度下炉内的燃烧过程进行了数值模拟，其结果为某企业常压炉的运行监控提供了参考依据。Nishimura M等[6]采用蓄热式烟气余热回收装置，用烟气余热对空气进行预热，最大程度的回收了高温烟气中的显热，使排烟温度下降到 150℃左右。巨大的余热回收潜力使得工业炉平均节能30%以上，某些高效节能炉甚至达到55%。

目前，针对采用天然气加热炉实物模型作为研究对象，并同时考虑燃烧参数对燃烧性能及介质传热影响的研究较少。本文以一台设计负荷为130kW的圆筒式天然气加热炉为研究对象[7]，针对不同的空气氧化剂预热温度，通过ANSYS FLUENT软件对火筒内的燃烧过程及整个加热炉的传热过程进行数值模拟，得到加热炉内温度场和浓度场的分布规律，为天然气加热炉的实际运用和优化设计提供了参考依据。

1 圆筒式天然气加热炉结构

圆筒式天然气加热炉是将燃料燃烧产生的热量传给被加热介质而使其温度升高的一种加热设备，它的结构如图 1(a)所示。被加热介质（天然气）在壳体内的对流管束中，由充满炉内空间的中间载热介质（如水，乙二醇或导热油[8-10]）加热对流管束中的气体，而中间载热介质由火筒直接加热。火筒是火管和烟道管束的总称。在火筒中，具有燃烧室功能，而且主要传递辐射热的加热部件称为火管；与火管相连通，且主要传递对流换热的加热部件称为烟道管束。

图1 (a)气体加热炉结构简图Fig.1 (a) structural diagram of gas heating furnace

燃烧器采用套筒式进料方式，如图 1(b)所示。内圈为燃料气进口，外圈为空气进口，燃料气和空气均沿竖直方向进入火筒[11-13]。该燃烧器的燃料气和空气在喷嘴外一边混合一边燃烧，其燃烧性能主要取决于进口燃料气和空气的温度、角度和速度等。

2 模型建立

2.1 物理模型与网格划分

本文对天然气加热炉进行了合理的简化，使用SolidWorks软件建立了物理模型。图2（a）为天然气加热炉的三维物理模型图。图2（b）为Y=-0.255 m处加热炉截面图。各部件的尺寸和规格列于表 1。在具体实验过程中，为了获得对流管束出口处的排烟温度，采用了JNT公司的infra-view红外线炉膛温度计对排烟温度进行了测量。该温度计采用非接触测量，测量温度范围是120℃～1650℃，测量精度可达1%，可以对加热炉运行过程中的排烟温度进行实时检测[14,15]。

图2 (a)天然气加热炉三维物理模型Fig.2 (a) 3D physical model of natural gas heating furnace

表1 燃气加热炉规格Tab.1 specification of gas heating furnace

选择ICEM软件对物理模型进行非结构化网格划分，并对燃烧器和各进出口面进行局部网格加密。通过网格无关性检验，确定最佳网格数为11609508。

2.2 求解模型选择

湍流模型选择标准 k-ε双方程模型，辐射模型分别采用DO模型和P-1模型，燃烧模型选择非预混扩散燃烧模型，NOx模型选择热力型NOx模型。其中，在非预混燃烧模型中计算分子间化学燃烧反应速率常用公式为阿伦尼乌斯公式(Arrhenius Equation)[16-18]。例如，燃料与氧气的反应速率为：

式中，0A为前置因子，E称为实验活化能，一般可视为与温度无关的常数，其单位为kJ/mol；R，摩尔气体常数，单位J/mol K⋅；E/R为活化温度；T为反应温度。

标准k-ε双方程模型由一个精确方程（k方程）和一个由经验公式推导出来的方程（ε方程）组成，它们分别为：

湍流动能k方程：

湍动能耗散率ε方程：

2.3 边界条件

天然气加热炉内流动的气体可看作不可压缩流体，且假设火筒内燃烧过程为稳态燃烧。火筒内的燃料为天然气，其组成成分及低位发热量如表2所示。由于天然气加热炉的设计负荷为130 kW，燃料的低位发热量为50660.7 kJ/kg。因此，燃烧器燃料质量流量为0.0026 kg/s。理论空气量与燃料流量之比为14.56，得到理论空气量为0.038 kg/s。过剩空气系数设为1.2，得到实际空气量为0.046 kg/s。燃料入口和空气入口均采用速度入口边界条件，则进一步可算得燃料入口速度为 32.9 m/s，空气入口速度为9.3 m/s。且设定燃料入口压力为0.12 MPa，空气入口压力为8 kPa。烟气出口设为压力出口边界条件，出口压力设为-20 Pa。

表2 燃料气质量分数和低热值Tab.2 Fuel gas mass fraction and low calorific value

对流管束内流动的为被加热介质，其中设定对流管束入口为速度入口边界条件，入口速度为1.67 m/s，入口压力为5.5 MPa，温度为280 K[19]。对流管束出口设为压力出口边界条件。为了能够在模拟燃烧的同时得出中间载热介质和对流管束的温度场，将火筒和对流管束壁均设为耦合壁面，燃烧器壁面和圆筒壁设均为绝热壁面。压力-速度方程的耦合方法选择Coupled算法。

根据上述的物理数学模型及边界条件等的设置，通过ANSYS FLUENT软件进行模拟。将烟道管束出口处的烟气数据模拟结果与实测值作比较，其相对误差的绝对值均小于10%，验证了模型及条件设置的合理性。比较结果如表3所示。

表3 模拟数据和测量值的比较Tab.3 Comparison of simulated data and measured value

3 计算条件及结果分析

3.1 计算条件

在加热炉几何结构不变的前提下，提高燃料气、空气的预热温度，可以显著增加理论燃烧温度，从而提高加热炉的整体传热效率。在燃料气温度为300 K，空燃气射流参数均不变的条件下，选取空气预热温度分别为300 K、400 K、500 K和600 K研究加热炉内温度场和浓度场分布。

3.2 结果分析

（1）温度场分析

图 3和图 4中(a)、(b)、(c)、(d)四个图分别对应的是在DO和P-1辐射模型下，空气预热温度分别为300 K、400 K、500 K和600 K时，在Y=-0.255 m截面处的温度分布云图。从图中可以看出，不管是采用DO还是P-1辐射模型，各空气预热温度下所对应的温度云图趋势基本相同，说明采用这两种辐射模型可以起到相互验证模拟结果的作用。当空气的预热温度为300 K时，燃料燃烧都发生在火管的中部，燃烧区离燃烧器的距离相对较远，燃料的着火过程出现明显的滞后，且燃烧区域狭小。随着空气预热温度的升高，燃料的着火过程逐渐提前，高温燃烧区出现在火管的前端，且燃烧体积逐渐变大。这是因为高温空气加快了燃料和氧化剂的反应速率，并使得达到燃烧条件的燃气量增多。在空气预热温度达到400 K时，火筒内出现明显的弥散状火焰，燃烧区域基本充满整个火管，火管和烟道管束内的温度分布也趋于均匀，这有利于燃料的充分燃烧。而当空气预热温度从400 K升高到600 K时，虽然着火过程不断提前，但是燃烧区域却逐渐减小。这主要是因为随着空气预热温度的升高，空气和燃料气的温差也不断的增大，这导致燃烧反应越来越不稳定，过高的空气预热温度使得燃料在燃烧器出口附近便已迅速完成燃烧，致使火筒内出现局部过热，火筒整体温度分布不均，并且火筒壁局部过热区容易发生烧穿现象。

图5显示的是在不同空气预热温度下燃料燃烧的放热量和对流管束内被加热气体的吸热量。从图中可以看出，随着空气预热温度的提高，DO和P-1辐射模型下放热量和吸热量均呈现先升高后降低的趋势。当空气预热温度从300 K升至400 K时，DO模型下燃料燃烧放热量从117.8 kW上升至128.3 kW，对流管束内被加热气体吸热量从 98.9 kW 上升至112.6 kW；P-1模型下燃料燃烧放热量从115.2 kW上升至124.7 kW，对流管束内被加热气体吸热量从88.5 kW上升至107.9 kW。燃料燃烧放热量越高，即表明燃料燃烧充分，而对流管束内被加热气体吸热量越多，即表明加热炉内中间载热介质的传热效率越高。这说明随着空气预热温度从300 K上升至400 K，燃料的燃烧更加充分，中间载热介质的传热效率也越来越高。而当空气预热温度从400 K上升至600 K时，燃烧放热量和被加热气体吸热量都在不断减小，说明当空气预热温度大于400 K时，继续升高预热温度并不能促进燃料的充分燃烧和中间载热介质的传热，反而降低了燃烧放热量和对流管束中被加热气体的吸热量。结合图3和图4的温度云图可知，过高的空气预热温度，导致燃料过早燃烧，且燃烧不充分，火筒内出现局部过热，火筒整体温度分布不均，进而导致中间载热介质受热不均，炉内介质流场混乱，传热效率降低。

图3 采用DO模型时在Y=-0.255 m截面处不同空气预热温度下的温度云图Fig.3 Temperature nephogram of different preheating temperature of air at y = -0.255 m section with DO model

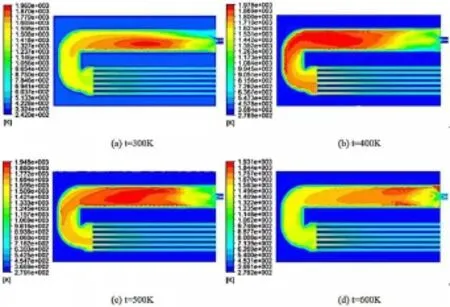
图4 采用P-1模型时在Y=-0.255 m截面处不同空气预热温度下的温度云图Fig.4 Temperature nephogram of different preheating temperature of air at y = -0.255 m section with P-1 model

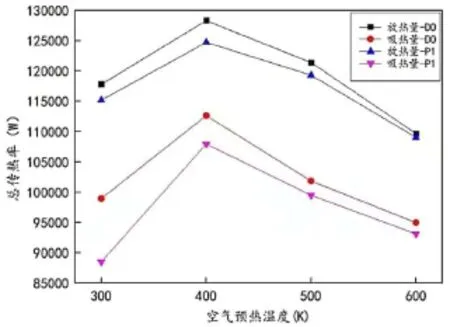
图5 不同空气预热温度下燃料燃烧放热量与对流管束内被加热气体吸热量Fig.5 Heat release from fuel combustion and heat absorption of heated gas in convection tube bundle under different air preheating temperature

图6 所示的是当燃料温度为300 K，空气预热温度分别为300 K、400 K、500 K和600 K时，烟道管束出口处排烟温度的模拟平均值与实验测量平均值的结果比较。其中的温度平均值是指24根烟管出口处排烟温度的平均值。从图6可以看出，烟道管束的排烟温度在DO模型和P-1模型下的模拟平均值与实验测量平均值吻合较好，说明模拟结果具有合理性。由于忽略了燃烧器壁和圆筒壁的散热，所以烟道管束排烟温度的模拟值一般比实验测量值高1-10 K。

图6 排烟温度模拟平均值和实验测量平均值比较Fig.6 Comparison between simulated average value and experimental average value of exhaust gas temperature

（2）浓度场分析

图7所示的是在不同空气预热温度下烟道管束出口排放的NOx浓度值。从图中可以看出在空气的预热温度从300 K上升至600 K的过程中，NOx的排放量不断增加。这主要是因为随着空气预热温度的升高，火筒内的高温区大大促进了热力型NOx的生成。在DO模型下，助燃空气预热温度从300 K上升至400 K时，NOx的生成速率还不大，空气预热温度达到400 K时烟道管束出口处的NOx浓度约为118 mg/m3，仍低于国家排放标准150 mg/m3。但当空气预热温度大于400 K时，NOx的生成速率迅速上升，空气预热温度达到500 K时NOx的排放浓度已达 175 mg/m3，超出烟气中氮氧化物排放浓度的国家标准。同样的，在 P-1模型下，空气预热温度在400 K时NOx的排放浓度仅为127 mg/m3，但600 K时NOx的排放浓度便达到了190 mg/m3。结合温度云图及燃料燃烧放热量和被加热气体吸热量的数据图可知，适当地升高空气预热温度，能够在不过多的生成 NOx的同时提升燃料燃烧的充分性和稳定性，进而增加燃烧放热量和被加热气体的吸热量，但是过高的空气预热温度则会使NOx的排放量迅速增加，对环境保护不利。从以上分析可知，空气预热的最佳温度为400K，在此温度下燃料燃烧最充分，燃烧放热量和对流管束内被加热气体吸热量最高，且烟管束出口排放的NOx浓度符合国家标准。因此在天然气加热炉的实际操作过程中，应该在满足污染物排放标准的情况下选取促进燃料燃烧和介质传热的最佳空气预热温度，以达到节能环保的目的。

图7 不同空气预热温度下烟道管束出口处NOx的浓度Fig.7 NOx concentration at the outlet of flue tube bundle under different air preheating temperature

4 结论

通过数值模拟不同空气预热温度下天然气加热炉的温度场和浓度场，分析得出以下结论。

（1）提高助燃空气的预热温度，燃料的着火过程提前，火焰高温区域面积增大，整个火筒的温度分布趋于均匀。但是过高的空气预热温度会使得燃料过早燃烧完全，并在燃烧器出口处出现局部过热区，易发生火筒壁烧穿现象。

（2）无论是采用DO辐射模型还是P-1辐射模型，随着空气预热温度的提高，燃料燃烧放热量和对流管束内被加热气体吸热量均呈现先升高后降低的趋势，且最高值均出现在预热温度为 400K时，即在此温度下，燃料燃烧最充分，中间载热介质的传热效率最高。在烟道管束出口处排烟温度的模拟平均值和实验测量平均值吻合较好，说明模拟结果具有合理性。

（3）NOx的排放浓度随着空气预热温度的升高而不断升高，当空气预热温度为 400K时，DO和P-1辐射模型下的 NOx排放浓度分别为 118mg/m3和127 mg/m3，均低于国家标准150 mg/m3。

（4）综合以上分析可知，130kW天然气加热炉的最佳空气预热温度为400K，在工程实际中，可以将天然气加热的助燃空气预热至 400K左右，以达到节能环保的目的。