利用环上容错学习问题构造可链接环签名方案*

叶 青，王文博，李莹莹，秦攀科，赵宗渠，王永军

河南理工大学 计算机科学与技术学院，河南 焦作454000

1 引言

环签名的概念由Rivest 等[1]在2001 年首次提出。该方案允许签名者匿名选择一个签名组。签名者对消息进行签名，验证者仅能确定签名者为组中一员，但无法确定哪一个成员。2004年，Liu等[2]在环签名中引入了一种称为可链接性的扩展属性，相应的环签名方案现在被称为可链接环签名。可链接环签名在保持签名者匿名性的同时，能够检测出两个环签名是否由同一签名者（使用同一私钥）生成。可链接环签名在加密货币、电子选举、电子现金等应用场景[3-5]中有重要应用。2007 年，Au 等[6]将基于证书的密码体制（certificate based cryptography，CBC）与可链接环签名结合，提出了一种基于证书的可链接环签名方案。2013 年，Liu 等[7]将可链接环签名的安全性进一步提高，提出了无条件匿名的可链接环签名方案（以往的可链接环签名方案的匿名性均为计算匿名性）。

然而，上述环签名（可链接环签名）方案都是基于经典的数论难题假设（如离散对数难题[8]和大整数因子分解难题[9]），由于这类难题存在高效的量子破译算法[10]，如果未来量子计算机成熟，基于经典数论难题的密码体制将不再安全。这种情况下，密码领域的学者们开始研究后量子密码学。在这些替代方案中，基于格的密码学由于其高效简单、高度可并行化，并可提供强有力的可证明安全保证而备受关注。文献[11]提出了一种高效的基于格的环签名，但是主要缺点是公钥、私钥及签名长度较大。文献[12]基于格上弱伪随机函数（weak pseudo random function，wPRF）、累加器和零知识证明构建了第一个格上可链接环签名方案。该方案的安全性基于小整数解（short integer solution，SIS）难题假设[13]。文献[14]基于理想格上同态承诺方案和∑-协议框架[15]，构建一个理想格上可链接环签名方案，并基于理想格上最短向量问题（shortest vector problem，SVP）证明方案的安全性。文献[16]基于格上抗冲突的哈希函数构建了一个格上可链接环签名方案，方案的安全性基于模格小整数解（module short integer solution，Module-SIS）困难问题（SIS 困难问题的变体）和模格容错学习（module learing with errors，Module-LWE）困难问题（LWE困难问题的变体）。

最近，文献[17]基于BLISS（bimodal lattice signature scheme）[18]构造了一个格上无条件匿名的可链接环签名方案。该方案基于环上小整数解（ring short integer solution，RSIS）[19]困难问题，其签名长度为O(N)。一般来说，格上密码方案常用的困难问题是SIS 和容错学习问题（learing with errors，LWE），但是基于LWE困难问题的格上密码方案通常存在密钥尺寸过长，密文空间较大，效率较低的问题，而RSIS 和环上容错学习问题（ring learning with errors，RLWE）[20]（由Lyubashevsky等2010年提出）两个困难问题分别是SIS 和LWE 难题在环上的改进版本，在相同的安全程度下，基于RSIS 和RLWE 难题的密码方案比基于SIS 和LWE 难题的密码方案所需的密钥长度更短，计算速度更快。

为解决格上可链接环签名方案的密钥尺寸过长，效率较低问题，本文基于RLWE 难题，依据文献[14]的技术路线，重新构造一个格上可链接环签名方案并提出一个应用场景——简易的数字货币模型。与文献[15]不同的是，文献[14]首先构造一个理想格上的同态承诺方案，然后结合∑-协议、Fiat-Shamir转化方法来构造可链接环签名，而本文是首先构造一个基于RLWE 难题的多项式环上的同态承诺方案，然后结合∑-协议、Fiat-Shamir 转化方法来构造可链接环签名。与以往格上可链接环签名方案相比，由于所提方案基于RLWE 困难问题构建，不但可规约至格上困难问题，抵抗量子计算机攻击，且由于环元素取自小多项式，方案具有更短的密钥尺寸和更高计算效率，且方案描述更简单。

2 符号说明

为表述方便，对本文的符号进行说明，如表1所示。

Table 1 Symbol description表1 符号说明

除了表1 中的符号，文中还用到O、、ω等符号，为常用计算复杂度符号。

3 预备知识

3.1 格

定义1（格）设b1,b2,…,bm是n维欧式空间ℝn上m个线性无关向量，格Λ定义为所有这些向量的整系数线性组合，即Λ=，其中向量组b1,b2,…,bm称为格的一组基。

定义2（格上离散高斯分布）对任意σ＞0，定义以向量c为中心，σ为参数的格Λ上的离散高斯分布为DΛ,σ,c(y)=，其中y∈Λ，ρσ,c(y)=。

3.2 RLWE问题

Lyubashevsky等[20]于2010年提出RLWE问题，并指出多项式环理想格最坏情况下近似最短向量问题（approximate shortest vector problem，aSVP）可量子归约至计算性RLWE 问题，而计算性RLWE 问题可一般规约至判定性RLWE（decision ring learning with errors，DRLWE）问题。

定义3（RLWE分布）对于安全参数n，令f(x)=xn+1 为n次首一不可约多项式，其中n是2的次幂；令q=1 mod 2n是一个足够大的素数，设多项式环R=Z[x]/f(x)，Rq=R/qR。误差分布χ为Rq上的高斯分布。设s∈Rq为秘密值，随机均匀选取a←Rq，从高斯分布随机选取e←χ，计算b=a∙s+e，输出(a,b)，由(a,b)所构成的新分布定义为As,χ，而Rq×Rq上的均匀分布定义为U。

定义4（计算性RLWE 问题假设）从As,χ分布中取一组互相独立的变量(a,b=a∙s+e)，求解其中包含的值s，即给定a、b恢复多项式s在计算上是不可行的。

定义5（判定性RLWE 问题）由(a,b=a∙s+e)产生的分布As,χ与Rq×Rq上的均匀分布U是计算不可区分的，即判定参数(a,b)是取自分布As,χ还是取自均匀分布U的概率是可忽略的。

定义6（β有界分布）如果一个分布χ满足Pre←χ[||e||∞＜β]≤1-negl(n)，则称其为β有界分布。

3.3 安全模型

本节给出安全模型及相关的安全定义。

3.3.1 可链接的环签名

一个可链接的环签名方案[7，21]由5 个概率多项式算法(Setup,KGen,Sign,Vfy,Link)组成。

（1）Setup(1n)：输入安全参数n，输出公共参数pp。

（2）KGen(pp)：输入安全参数pp，生成用户验证密钥vk和签名密钥sk。

（3）Sign(ski,U,μ)：输入环U，签名者的私钥ski，消息μ，该算法输出环U对消息μ的签名σ。

（4）Vfy(μ,U,σ)：输入环U，消息μ及环签名σ，接受输出1；否则，输出0。

（5）Link(pp,σ,σ′)：输入公共参数pp，两个环签名σ、σ′，该算法用于验证两个环签名σ、σ′是否为同一个签名者产生。如果为同一签名者产生，则输出1；否则，输出0。

3.3.2 可链接环签名安全模型

下面分别给出匿名性、不可伪造性定义：

定义7（匿名性）如果消息μ在环U和密钥下的签名形式上与消息μ在环U和密钥下的签名完全相同，则可链接环签名方案(Setup,KGen,Sign,Vfy,Link)具有匿名性。正式地，要求任意对手A：

其中，A选择i0、i1，由密钥预言KGen(pp)生成并且。

定义8（不可伪造性）可链接环签名方案(Setup,KGen,Sign,Vfy,Link)是不可伪造的，如果攻击者A只知道公钥和消息签名对的情况下，对未询问的消息伪造环签名是不可行的，形式上对于所有概率多项式时间的攻击者A：

（1）第i个查询中VKGen随机选取ri，运行(vki,ski)←KGen(pp,ri)，返回vki；

（2）若(vki,ski)由KGen(pp,ri)生成且vki∈U，则Sign(i,μ,U)返回；

（3）A输出环签名(μ′,U′,σ′)，使得Sign没有被(μ′,U′,*)询问，并且U中仅包含由VKGen生成的密钥vki。

4 基于RLWE难题的可链接环签名方案

4.1 基于RLWE难题的同态承诺方案

对于RLWE难题，即从As,χ分布中取一组互相独立的变量(a,b=a∙s+e)，求解其中包含的值s，即给定a、b恢复多项式s在计算上是不可行的，如果把s看作被承诺消息，e看作随机数，这样则构造出一个基于RLWE难题的同态承诺方案[22]。具体地说，基于RLWE难题的同态承诺方案包括以下两个算法：

参数建立算法（KGen）：输入安全参数n，令Rq=Zq[x]/＜xn+1＞，其中q是一个足够大的公共素数，n是2 的次幂。随机选取元素a←Rq，设置消息空间为M=Rq，随机数空间R=Rq，生成Rq上的高斯分布χ，承诺空间为C=Rq，产生承诺密钥ck={a,n,q}。

承诺算法（Com）：输入一个待承诺消息s∈M，随机选取小的错误向量e∈R，e服从χ分布且||e||∞≤β，β是一个正整数，计算承诺c=a∙s+e∈Rq。

定理1（所提承诺方案满足隐藏性）

证明由计算性RLWE 问题可知，对于给定若干组独立的(a,b=a∙s+e)，计算出s是不可行的（具体安全证明参考文献[20]），因此所提承诺方案的隐藏性是显而易见的，即给定承诺值c，想计算出被承诺消息s，在计算上是不可行的。 □

定理2（所提承诺方案满足绑定性）

证明令s=ω(lbn)，β＜q/2d（d=φ(n)为欧拉函数），所提方案满足绑定性。假设对于不同的消息s0、s1，可得到同一承诺值c，即对于c0=Com(s0;e0)，c1=Com(s1;e1)，有c0=c1。由于每个ei=c-asi(i=0,1)的无穷范数至多为β，因此对于e0-e1=a(s1-s0)无穷范数有||e0-e1||∞≤||e0||∞+||e1||∞＜2β。由于a是从Rq中均匀随机选取的多项式，根据文献[23]（引理21），可以把多项式环a的系数a看作是整数矩阵A中的一个列向量，对于任意的非零向量x∈，则存在很大的概率选择向量a，有||ax||∞≥2β，这与||e0-e1||∞＜2β矛盾，因此本文承诺方案满足绑定性。 □

定理3（所提承诺方案满足同态性）

证明假设s0,s1∈M，e0,e1∈R，有以下等式：

故所提承诺方案满足多项式环上的加法同态性。□

4.2 基于RLWE承诺的可链接环签名方案

本文基于RLWE承诺方案，依据文献[14]的技术路线，重新构造一个格上可链接环签名方案。与文献[14]不同的是，本文是基于4.1 节的RLWE 同态承诺方案，并结合∑-协议、Fiat-Shamir转化方法来构造可链接环签名，而文献[14]是基于理想格上的同态承诺方案，结合∑-协议、Fiat-Shamir[24]转化方法来构造可链接环签名。

基于RLWE 承诺的可链接环签名（linkable ring scheme based on RLWE，R2LRS）包括五个算法(Setup,KGen,Sign,Vfy,Link)，具体描述如下：

Setup(1n,N)：输入安全参数n，环成员个数N，调用4.1 节同态承诺方案的KGen算法，产生承诺密钥ck={a,n,q}，消息空间为M=Rq，随机数空间R=Rq和承诺空间为C=Rq，选择一个散列函数H:{0,1}*→{-1,0,1}n，最终输出pp=(n,q,H,a,N)。

KGen(pp)：对于第ℓ 个用户，随机选取s←Rq且随机抽样一个差错e←χ，计算cℓ=as+eℓ，令第ℓ 个用户的验证公钥vkℓ=cℓ，签名私钥skℓ=eℓ。

Sign(pp,eℓ,μ,U)：设U=(c0,c1,…,cN-1)是环成员公钥的集合，在输入消息μ时，第ℓ 个用户代表U生成的签名如下。

（1）计算Iℓ=aeℓ；

（2）对于j∈{1,2,…,n}，其中n=，随机选择rj,uj,yj,tj,ρk←Rq。

计算：

土老帽：“哈哈哈！看大家说得如此热闹，我也忍不住看了一下，觉得有些感慨，在手机照相流行的今天，除了全家福、大合照、结婚照一类的有特殊意义的照片会冲印出来，大家现在很少会把照片洗出来，放在相册里留待翻看。想想以前爸妈帮我们拍照，再去照相馆精心选出来，那种期待的心情，之后回想起当时的场景，感受到亲人的陪伴，生活的有趣，与现在拍照一秒钟，精修美颜一小时的心情，截然不同了。拍照其实是次要的，我们更需要去关注的是身边的人，更需要去感受和发现的是身边的趣和美。这才是生活啊。”

（3）对于j∈{1,2,…,n}，计算：

①fj=xℓj+uj

令S2=，公开σ={S1,S2,zw,Iℓ,U}作为第ℓ 个用户对消息μ的环签名。

Vfy(pp,μ,U,σ)：

（2）对应j={1,2,…,n}，判断以下是否成立：

③xnIℓ+

如果其中任何一个不成立，输出0 并中止；否则输出1。

Link(pp,σ,σ′)：对于两个签名σ=(…,I,U)和σ′=(…,I′,U′)，如果I=I′，返回1（可链接）则是同一个签名者产生；否者返回0（不可链接）。

5 安全性与效率分析

5.1 安全性分析

下面将对方案的安全性进行分析。

正确性：假设一个由Sign算法产生的环U关于消息μ的签名为σ={S1,S2,zw,Iℓ,U}，其中，则必有∈Cck，f1,…,zw∈Rq，且：

即Vfy算法中的等式①成立。

即Vfy算法中的等式②成立。

即Vfy算法中的等式③成立。

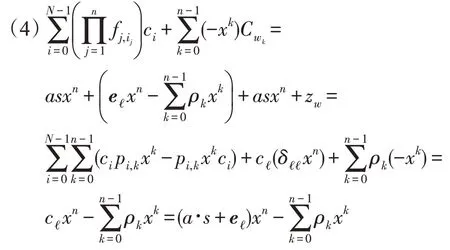
当s=0 时，，即Vfy

算法中的等式④成立。

可链接性：关于本文所提可链接环签名方案的可链接性由以下定理刻画。

定理4假设使用N个签名密钥SK={e0,e1,…,eN-1}产生N+1 个签名，这些N+1 个签名中有两个签名由同一签名者产生，其余N-1 个签名均分别由其他签名者产生，则同一签名者产生的两个签名可通过链接算法，其他签名均不能通过链接算法。

证明假设敌手可以产生N+1个有效的签名σi=，使得Ii是两两不同的，其中i∈{0,1,…,N}。因为|SK|=N（|SK|表示签名密钥集合中元素的个数），所以至少存在一个Ii不属于集合{aej:ej∈SK}。为了不失一般性，对于π∈{0,1,…,N}，假设这种情况在σπ上发生，由于σπ是一个有效的签名，从验证等式有：

定理5假设承诺方案满足隐藏性，则本文提出的环签名方案具有匿名性。

证明首先假设攻击者A得到签名σ，从签名本身σ和消息μ∈Rq，攻击者不能识别签名者身份。由于任何一个环成员都具有生成签名的能力，因此从具有n个成员的环中识别实际签名者的概率不超过1/n。

而对于本文的承诺方案c=ais+ei具有隐藏性，不会泄露被承诺的消息s。由于s、e是在各自的空间均匀随机选取，则计算得到承诺c的分布是伪随机的。另一方面由∑-协议的见证不可区分性（文献[15]定义8），保证了不可能区分使用哪个密钥来生成环签名。因此可以得出承诺方案具有隐藏性，环签名方案满足匿名性。 □

定理6假设所提承诺方案满足隐藏性和计算绑定性，则本文环签名方案是不可伪造的。

证明考虑一个多项式时间攻击者A，将散列函数H视为预言机，对VKGen、Sign和随机预言至多为qV(n)、qS(n)和qH(n)次查询，并且对于无穷多个n∈N 具有至少1/p(n)的概率来攻破正多项式p的不可伪造性。将证明它可以用来构造一个多项式时间攻击，该攻击在极多的λ∈N中以约1/2qV(λ)p(λ)的机会破坏承诺方案的绑定属性。

当A查询VKGen时，按照环签名方案运行，在第j个查询中返回vkj。如果A查询Sign(j,μ,U)，随机选择x←{0,1}n并使用特殊的诚实验证者零知识模拟器（文献[15]，定义7）来模拟证明{S1,S2,zw,Iℓ,U}。然后通过随机预言H(∙)计算H(pp,μ,U,S1,Iℓ)=x，如果H(pp,μ,U,S1,Iℓ)之前已经查询过，在这种情况下中止。

最后，A尝试在环中创建伪造的环签名，其中签名不是来自签名预言，即(μ′,U′,*)未被询问过。如果A无法创建伪造，将会停止。否则，使用来自用于获取挑战值x(0)的随机预言查询H(pp,μ,U,S1,Iℓ)的环U在μ上获得成功的伪造环签名σ={S1,S2,zw,Iℓ,U}。现在将攻击者倒回到进行伪造签名使用的查询H(pp,μ,U,S1,Iℓ)的位置，并随机回答预言查询，直到它使用相同的查询生成n个额外的带有挑战x(1),x(2),…,x(n)的伪造环签名。如上所述，在每次倒回中，如果对签名的模拟导致对预言查询的重用，则中止。此外，如果倒回次数超过2p(λ)n，则停止。

如果倒回后的攻击者对总共n+1 个不同的挑战给出了答案，现在可以使用（n+1）-特殊的稳健性（文献[15]定理3）来打破承诺方案的约束属性或者打开某个vki=Com(0;ri)的(0;ri)。概率为1/qv时，有vki=vkj，这与承诺方案的绑定属性相矛盾。总之，对于无穷多的λ∈N，攻击有接近或高于1/2qV(λ)p(λ)的机会打破承诺方案的绑定性。因此承诺方案满足隐藏性和计算绑定性，则所提环签名方案是不可伪造的。 □

5.2 效率分析

本节将本文方案与基于格的环签名方案文献[11]、文献[14]在以下几方面进行比较。

表2中假设签名环中的成员个数为l（1＜l≤N，N为环的最大尺寸），n为输入的安全参数，q是大素数。文献[11]中m的取值范围为m≥5nlbq，文献[14]中m的范围为m=Θ(lbn)；在比较签名和验证代时，用˜表示计算复杂度，主要考虑耗时较长的矩阵乘法和多项式乘法运算，忽略hash 函数等耗时较少的运算。具体比较结果如表2所示。

Table 2 Efficiency analysis and comparison表2 效率分析对比

在公私钥尺寸方面，文献[11]采用的是GPV08陷门函数生成的小基作为私钥，文献[14]则随机选取矩阵Xi∈Dm×m作为私钥，而本文方案采用小整数多项式作为私钥，并且系数范围较小，而对于公钥，文献[11]通过GPV08 格点筛选算法生成公钥，文献[14]和本文方案分别通过矩阵和小多项式乘法得到公钥，表2显示本文公私钥尺寸小于上述两个方案。

在签名长度方面，文献[11]中m的取值范围m≥5nlbq，因此n(5l+10)lb2q＞n(10+l)lbq=m(l+2)lbq≥5n(l+2)lb2q，显然文献[11]的签名长度大于本文方案签名长度；而文献[14]中m一般情况下都是大于1的，因而文献[14]签名长度也大于本文方案的签名长度。

在签名运算代价方面，文献[11]采用陷门函数、格基生成算法，涉及计算代价较高的矩阵求逆操作，而本文方案没有涉及陷门函数，因此文献[11]签名效率低于本文方案。

对于Rq上的一个元素u(x)=u0+u1x+…+un-1xn-1，可以将其写成向量形式u=(u0,u1,…,un-1)，向量u维数为n，且每个分量项都是模q得到。由于本文方案中私钥是在Rq上随机选取的n维多项式（n维向量），因此私钥长度为nlbq，而公钥也是n维向量，公钥长度也为nlbq。此外，环Rq中2 个元素相乘，相当于并行进行了n次向量内积。涉及到多项式环乘法运算可以通过快速傅里叶变换来实现，这也会很大程度上提高方案的效率。综合比较，本文方案效率优于文献[11，14]，具有更低的存储空间和更高的计算效率。

6 应用场景——简易的数字货币模型

本章基于RLWE 难题的可链接环签名（R2LRS）提出一个新的数字货币模型。采用文献[25]提出一次性目的地址技术，并且依据文献[14]的路线，重新构造一个基于R2LRS 的数字货币模型。该模型有4个算法，分别为系统建立、用户密钥生成、目的密钥生成、目的密钥恢复（其中目的密钥也称为一次性目的地址）。

系统建立：输入安全参数，运行R2LRS和公钥加密算法（文献[20]）进行初始化，生成整个模型的全部参数PP。

用户密钥生成：此算法产生两对公私钥(epk,esk)和(c,e)。

目的密钥生成：发送者选择一个随机数ep←χ并利用接收者密钥，来产生一次性目的地址cd=cp+c。除了接收者外，其他任何人无法恢复出完整的签名密钥。接着选择对称加密算法Enc和对称密钥k，首先用第一步中的公钥加密算法加密对称密钥k，然后利用对称加密算法加密hash(epk)||ep。

目的密钥恢复：对于接收者，首先利用私钥解密出对称密钥k，随后利用对称密钥k解密出hash(epk||ep)，进而提取出ep，计算，比较=cd，则说明cd是有效目的地址，ed是cd对应的有效签名密钥。

对于用户A、B，假设A把钱转给B，首先由系统给双方产生密钥对，A利用B的公钥产生一次性目的地址，然后产生公钥加密信息Enc(k)以及对称加密信息hash(epk)||ep，A另外收集其他N-1 个一次性地址，链接密钥，签名密钥用来生成可链接环签名，最后A输入金额、一次性目的地址、加密信息、环签名等信息进行哈希运算，最后A广播此信息。B检查接收到的交易，提取一次性目的地址，对加密信息进行相应的解密，利用目的密钥恢复算法，如果此交易是发送给B，则B接受该交易，提取对应的签名密钥ed，把cd、ed放入钱包，B随后可以花费cd地址的钱。

7 结束语

随着对抗量子攻击的密码方案关注度的提高，基于格的签名体制也逐渐成为研究热点。本文主要贡献是首先构造一个基于RLWE难题的多项式环上的同态承诺方案，然后结合∑-协议、Fiat-Shamir转化方法来构造可链接环签名，并且在随机预言模型下基于计算性RLWE 问题证明本文方案的安全性，同时给出详细的效率分析，最后基于本文方案提出了一个应用场景——简易的数字货币模型。接下来计划对本文方案进行实验分析，对应用场景作进一步的研究。