基于算理理解的定律模型教学策略

张梁 裘斐

【摘   要】建立模型是数学运用和解决问题的核心，要立足于学生理解算理的基础上。教学中教师可运用以下策略：多类材料，抽象模型;循序渐进，建立模型;分层练习，应用模型;举一反三，类比推理。让学生在经历抽象、应用、拓展的过程中，充分理解和正确运用乘法分配律，培养学生数学建模能力和推理能力，提高学生的数学综合素养。

【关键词】运算律;教学;策略

运算定律在计算以及解决实际问题中起着重要的作用，对小学生来说，正确运用运算定律不易，尤其是乘法分配律，学生极易出错，是一个教学难点。通过分析发现，由于学生未能充分理解乘法分配律的算理，缺乏完整的建模过程，导致问题出现。以下是笔者对人教版四年级下册“乘法分配律”一课的教学研究，重在以算理构建运算定律的模型。

一、教学过程及问题分析

【案例呈现】

1.情景导入。一共有25个小组，每组4人负责挖坑、种树，2人负责抬水、浇树。求一共有多少人参加植树活动？

2.探究新知。学生列出等式（4+2）×25=4×25+2×25，再列举类似的等式，归纳出乘法分配律的规律，并用字母表示。

3.巩固练习。简便计算练习：54×3+54×7;36×101。

虽然课堂上学生练习的正确率还算高，但课后测评作业情况不容乐观，说明学生在乘法分配律的理解上还存在一定的缺陷。

【问题分析】

笔者对学生的课后测评情况加以统计并进行了问题分析。

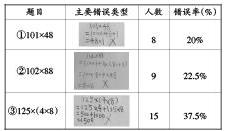
问题1：分配不全。第①题学生已经关注到把101拆分成“100+1”，但是没有考虑算式的意义，“101×48”表示101个48，而“100×48+1”却表示100个48多1，误把“1×48”写成了“1”，忽略“一个几”的乘法意义。

问题2：缺少相同乘数。第②题学生把两个乘数同时进行了拆分，将102拆分成“100+2”，88拆分成“80+8”。这样的拆分缺少相同的乘数，显然学生是在死板地套用乘法分配律的形式，对于乘法分配律模型的理解不够。

问题3：混淆运算定律。第③题错误率最高，学生将乘法结合律和乘法分配律混淆，无法辨析两者的意义和形式，算理和算法脱节，解题受到表象的干扰。

笔者认为，这样的教学轻视了乘法分配律意义的理解，构建乘法分配律模型的过程比较模糊，造成部分学生对于乘法分配律的理解滞留在表面，注重结构记忆，缺乏系统化的认识。

二、以算理构建运算定律模型的教学策略

（一）多类材料，抽象模型

《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）指出：“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。”因此教师可以选取贴近学生生活经验的不同材料，借助熟悉的生活事例以及直观图得出等式，以帮助学生明确算理，感知乘法分配律模型。

人教版教材通过创设情境图提出不同的问题，将乘法交换律、乘法结合律、乘法分配律贯穿一线，这样的编排有利于教学资源的整合，能培养学生有效选择信息、解决问题的能力。但是笔者认为，由于题目中的信息量较大，容易混淆，反而不利于聚焦研究的重点。因此笔者在教学时选择了以下两种学习材料。

1.生活材料

创设学生熟悉的生活情境作为教学切入点，激发学生主动学习的需要，帮助学生搭建新旧知识沟通的桥梁，使“事理”上升到“数理”。

材料1：

某运动服装专卖店中一套运动服的价格是80元，昨天卖了6套，今天又卖了4套，那么一共赚了多少钱？

①（6+4）×80=800元     ② 6×80+4×80=800元

得出等式：

（6+4）×80=6×80+4×80

10个80=6个80+4个80

材料1借助生活情境，让学生解释算式：“10套衣服的钱就是6套衣服的钱加上4套衣服的钱。”并可以将此理解为：10个80等于6个80加4个80。由此学生初步抽象出乘法分配律模型。

2.直观材料

中段學生的抽象思维能力还比较薄弱，往往说理的时候表达不清楚，教师可以借助直观的几何图形，通过数形结合的方式，帮助学生直观而有效地抽象出乘法分配律模型。

材料2借助几何图形，让学生直观阐述算式的意义：“长加宽的和乘2等于长乘2加宽乘2。”由特殊到一般，从而归纳出有关周长公式的等式：周长=（长+宽）×2=长×2+宽×2 。教师随即追问：（长+宽）×2=长×2+宽，可以吗？学生结合图作出解释：不可以，因为等式左边求的是周长，而右边只算了两条长和一条宽，不是周长。通过图与算式的紧密联系，学生能更好地理解并抽象出乘法分配律模型。

[材料2：

某小学的操场是长方形的，长75米，宽25米，你能算出操场的周长是多少吗？

①（75+25）×2=200米   ②75×2+25×2=200米

得到等式：（长+宽）×2=长×2+宽×2]

（二）循序渐进，建立模型

叶圣陶先生曾说过：教是为了不教。学生要真正构建乘法分配律模型，需要经历丰富的数学活动过程，积累数学活动经验，从而提高学生的数学思维能力，使具象思维转变为抽象思维。

1.自主探究，初建模型

自主探索与合作交流是《课程标准》提出的学习要求，学生通过自主探究，能完善认知结构，建构数学模型，逐渐培养推理能力和建模能力。

【教学片段1】

师：你能模仿等式（6+4）×80=6×80+4×80列出类似的等式吗？

（学生独立列式。汇报交流时教师选择学生列举的3个等式板书在黑板上）

师：观察这4个等式，你发现了什么规律？先观察等号左边有什么相同的地方，右边呢？想一想，小组成员之间说说看。

生：左边的算式都有括号。

生：左边是先加后乘，右边是先乘后加。

生：右边的算式和左边的算式末尾的数都是相同的。

生：左边的算式都是括号里两个数加起来乘一个数，右边的算式是括号里的两个数拿出来与这个数相乘。

……

师（概括总结）：乘法分配律就是两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

学生在模仿列举等式的过程中，自然而然地完成了猜测与验证，接着通过自主探索、辨析交流，找出规律，说出等式左右两边的相同点，从而初步建立乘法分配律的模型，同时提高了分析、归纳、推理的能力。

2.知识联系，巩固模型

数学知识之间存在一定的联系，是一个完善的知识体系。笔者借助学生已有的知识经验，让学生经历列竖式计算的过程，将列竖式计算与乘法分配律运算紧密结合，因此巩固了模型。

【教学片段2】

师：请你在草稿纸上进行竖式计算25×12。

生：

师：在竖式计算过程中是否也运用了乘法运算定律？又是如何运用的呢？

生：运用了乘法分配律，把12拆分成了10和2，然后分别与25相乘，再把两个积相加。就是2个25加上10个25，表示12个25。

师：所以，我们也可以得到等式 25×（2+10）=25×2+25×10。（师板书）

学生通过经历完整的两位数乘两位数的计算过程，说出了竖式计算中如何运用乘法分配律：12拆分成2个10，分别与25相乘，也就是2个25加上10个25，表示12个25相加，由此巩固了模型，同时也提升了学生迁移运用知识的能力。

3.多种表征，理解模型

在抽象、初建、巩固模型的基础上，通过语言、文字、画图等方式表征模型，从具象到符号，促进学生深层次地理解模型，从而有效构建乘法分配律模型。

【教学片段3】

（1）读一读。

师：请大家读一读等式（6+4）×80=6×80+4×80，（75+25）×2=75×2+25×2。

生：6与4的和乘80等于6乘80的积加4乘80的积。

生：75与25的和乘2等于75乘2的积加25乘2的积。

（2）填一填。

教师出示如下式子，请学生填一填。

①（▲+■）×8=○×8+○×8

②（60+40）×★=60×○+40×○

（3）说一说。

教师出示如下式子，请学生说一说。

①（▲+■）×8=▲×8+■×8

②（60+40）×★=60×★+40×★

生：▲和■这两个数加起来乘8等于这两个数分别乘8，再加起来。

生：  100乘★等于60乘★加40乘★。

（4）写一写。

师：能用你喜欢的方式来表示这样的等式吗？

生：（△+☆）+□=△×□+☆×□。

生： （甲+乙）×丙=甲×丙+乙×丙。

生：（a+b）×c=a×c+b×c。

……

师：你们真了不起，能够用这么多不同的形式来表示乘法分配律！

师：你觉得哪种表示方法更简便？

生：用字母表示更简便。

学生通过读一读、填一填、说一说，感受这些等式都是“两个数的和乘一个数等于两个数分别乘一个数，再把两个积相加”的形式，巩固了乘法分配律的模型。最后教师让学生用自己喜欢的方式写一写乘法分配律模型，抽象出简洁的数学模型，增强学生的建模意识和符号意识，培养了数学语言表达能力。

（三）分层练习，应用模型

通过辨析判断，简便计算，解决生活实际问题，让学生在运用乘法分配律模型的基础上，提升数学应用能力。

如教师可出示以下练习：

①判断下列算式是否正确，正确的打“√”，错误的打“×”。

56×（19+28）=56×19+28         （  ）

32×（7×3）=32×7+32×3           （  ）

64×64+36×64=（64+36）×64   （  ）

②運用简便计算计算下列各题。

36×101                   48×99             54×3+54×7

③解决问题。

运动会上，老师给45位学生每人发了一瓶水和一个小蛋糕，水每瓶2元，小蛋糕每个8元，老师一共花了多少钱？

（四）举一反三，类比推理

学生熟练应用模型后，教师可尝试通过类比推理的方式进行拓展，让学生体验到学以致用的乐趣。

（1）乘法对减法是否也有分配律呢？例如：（6-4）×80=6×80-4×80等式成立吗？学生通过验证发现这一运算律同样适用于减法，并用算理解释：2个80等于6个80减去4个80。

（2）括号里的加数多于两个还成立吗？例如：（6+4+2）×80=80×6+80×4+80×2，学生通过验证发现这个等式也是成立的，同样用算理解释：12个80等于6个80加4个80加2个80。

参考文献：

[1]俞秉钧.乘法分配律问题的错误分析与矫正[J].基础教育研究，2015（6）.

[2]金水忠.构建数学模型，提升学生思维——“乘法分配律”教学例谈[J].数学大世界，2017（8）.

（浙江省杭州市余杭区临平第三小学   311100）