全曲线波形板-UHPC 组合桥面板优化设计

戴杜伟，刘扬，鲁乃唯

(长沙理工大学 土木工程学院，湖南 长沙 410114)

正交异性钢桥面板因其质量轻、强度高及跨越能力强等特点，在国内、外各类桥梁建设中应用广泛。正交异性钢桥面板结构焊缝数量多、构造复杂、焊接残余应力大[1]，在循环应力的作用下容易出现裂纹，对桥梁结构的服役寿命有影响。因此，疲劳问题已成为严重影响正交异性钢桥面板性能和使用寿命的关键性问题，如何提高其疲劳寿命是制约其推广应用的关键所在。

众多学者从材料性能、构造形式及构造细节等方面对正交异性钢桥面板的疲劳问题进行了研究。余波[2]等人选取某实桥钢桥面板的2 个疲劳细节进行了疲劳试验，发现疲劳裂纹首先在横隔板与纵肋焊接处的下部出现，纵肋与顶板焊接处疲劳损伤较大且均位于顶板外侧。张玉玲[3]等人针对钢桥面板的6 种疲劳细节进行试验，提出利用准热点应力统计来获取正交异性板构造细节的名义应力，并对增强正交异性板的疲劳设计验算方法的可操作性和准确性给出了建议。蒋永[4]等人对典型疲劳细节进行了疲劳性能分析，发现减少焊缝数量或提高焊缝强度能提高正交异性板结构的抗疲劳性能，并提出2 种改进后的构造细节的设想。Frýba[5]针对正交异性板结构进行了疲劳试验，发现开孔形状对结构的疲劳性能影响很大。苹果形开孔结构的疲劳性能比圆形开孔强，单圆孔与对称双圆孔结构的疲劳性能相同，非对称挖孔结构的疲劳性能最差。叶华文[6]等人对不同铺装层厚度、横隔板厚度和挖孔形式的正交异性板进行了疲劳性能研究，其结果表明：相比于挖孔形式，铺装层及横隔板厚度对结构疲劳性能的影响更大；苹果型开孔的疲劳性能最好。邵旭东[7]等人提出一种正交异性钢板与薄层UHPC 的组合结构，建立了有限元模型和足尺条带模型。通过静载试验，研究其受力性能。试验结果表明：新结构可明显提高桥面系刚度，减轻疲劳开裂的风险。苏庆田[8]等人提出一种折形钢板-混凝土组合桥面板结构，优化了其截面形式并进行了足尺桥面板加载试验，得出新结构的抗弯极限承载力远大于规范要求，验证了其用于工程结构的可行性。张清华[9]等人提出波形顶板-UHPC 组合桥面板结构，并采用BP 神经网络进行参数优化，优化后结构的疲劳性能相比传统正交异性板有明显提升，对解决正交异性板的疲劳问题提供了一种较好的解决方案。

学者们围绕着影响传统正交异性板疲劳性能的3 个因素提出了各类解决方案。针对材料性能因素，引入超高性能混凝土(Ultra-High Performance Concrete, 简称为UHPC)，以提升结构刚度；针对构造的形式和细节因素，提出新的结构形式，以减少结构的几何构型不连续(应力集中)和焊缝数量[10]。其中：波形顶板与UHPC 的组合桥面板结构能同时减少几何构型不连续部位和焊缝的数量，并提升结构刚度，是一种较好的解决方案，但由于其波形顶板结构的弯折处存在着应力集中现象，可能出现疲劳裂纹。作者拟提出一种全曲线截面形式的波形板-UHPC 组合桥面板结构(也称为“全曲线波形板-UHPC 组合桥面板”)，研究其设计参数对结构力学性能的影响，并利用响应面法对其设计参数进行优化，对比传统正交异性板，对结构的疲劳性能进行研究。

1 新型组合桥面板设计参数的确定及其影响规律

1.1 新型组合桥面板的介绍

针对传统正交异性板疲劳开裂，提出一种全曲线波形板-UHPC 组合桥面板结构。它由UHPC、波形钢板、组合销及横隔板组成，如图1 所示。相比传统正交异性板，这种结构用UHPC 代替钢桥面顶板，同时消除了顶板与U 肋及U 肋与横隔板的连接焊缝，取消了横隔板开孔，直接由UHPC、整体性的波形钢板及横隔板组合而成。其中，UHPC 与波形钢板由组合销连接，波形钢板与横隔板采用焊缝连接。此结构由于采用UHPC，增强了结构的整体刚度，减小了结构易损部位的应力幅。同时，只存在波形钢板与横隔板的焊缝，大幅减少了焊缝的数量。采用全曲线形式，降低了截面弯折处的应力集中程度，明显减轻了结构疲劳开裂的风险。该结构的截面形式如图2 所示。一个完整波形截面由4条完全相同的n次曲线组成：标准曲线的横向投影长度为a，纵向投影长度为b。

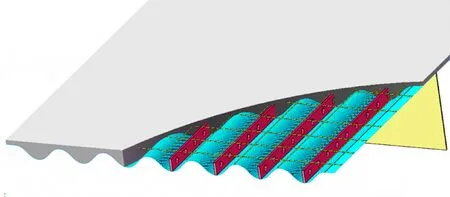
图1 全曲线波形板-UHPC 组合桥面板结构示意图Fig.1 Schematic diagram of wave plate-UHPC composite bridge deck with full curvilinear section

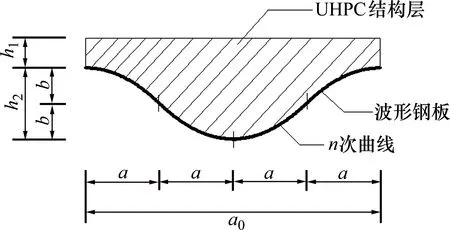
图2 全曲线波形板-UHPC 组合桥面的截面示意Fig.2 Section form of wave plate-UHPC composite bridge deck with full curvilinear section

1.2 有限元模型的建立

全曲线波形板-UHPC 组合桥面板结构的截面设计参数有：上部UHPC 结构层厚度为h1，波形板高度为h2，一个完整波形宽度为a0。由于一个完整波形由4 条标准曲线组成，由图2 可知，h2=2b，a0=4a。以波形最低点为原点，水平向右为x轴，竖直向上为y轴，则图2 中从左向右数的第三段曲线的数学表达式为：

式中：x为横向投影长度变量；y为纵向投影长度变量。

结合式(1)可知，该结构截面形式的关键设计参数为4 个：上部UHPC 结构层厚度h1、横向投影长度a、纵向投影长度b及曲线次数n。由于上部UHPC结构层自重较大，对结构的疲劳性能影响明显。h1取值过大会明显增加自重，取值太小会导致结构刚度不足。为简化分析，参考UHPC 组合桥面板的研究结果，将上部UHPC 结构层厚度h1的取值定为45 mm，仅对后3 个关键设计参数进行了研究。参考国内、外学者对传统正交异性板及UHPC 组合桥面板的研究结果，取横隔板高度800 mm，板厚14 mm，横隔板间距3 000 mm；参考普通正交异性板U 肋，波形板厚度取8 mm。

采用ANSYS 软件，建立了模型。由于正交异性板主要应用于大跨度桥梁结构，为使分析模型更接近实际工程结构的受力状态及边界条件状况，结构模型纵向长度取12 m(包含4 个横隔板间距)，横向截面宽度取7 个标准波形截面。UHPC 采用Solid45 实体单元，波形板和横隔板在纵向跨中0.5 m 范围内采用Solid45 实体单元，其余部分采用Shell63 板壳单元，跨中焊缝采用Solid45 实体单元。UHPC 与波形钢板由于使用组合销连接，可认为无相对滑移，处于完全粘接状态，故实体单元与板壳单元采用共节点方式进行连接，边界条件为对所有横隔板两端施加Y方向约束和Z方向转动约束，同时在最右部的横隔板两端施加X和Z方向约束。钢材取q345qd，弹性模量和泊松比分别为2.06×105MPa 和0.3；UHPC 取RPC200，弹性模量和泊松比分别为4.26×104MPa 和0.2。在结构最不利位置处进行加载，即沿纵向中间两跨跨中分别施加2 个车轮荷载，每个轮载70 kN，车轮面积为600 mm×200 mm，作为均布荷载施加。模型共有362 024 个单元(其中：实体单元325 680 个，板壳单元36 344 个)。有限元模型结构如图3 所示。

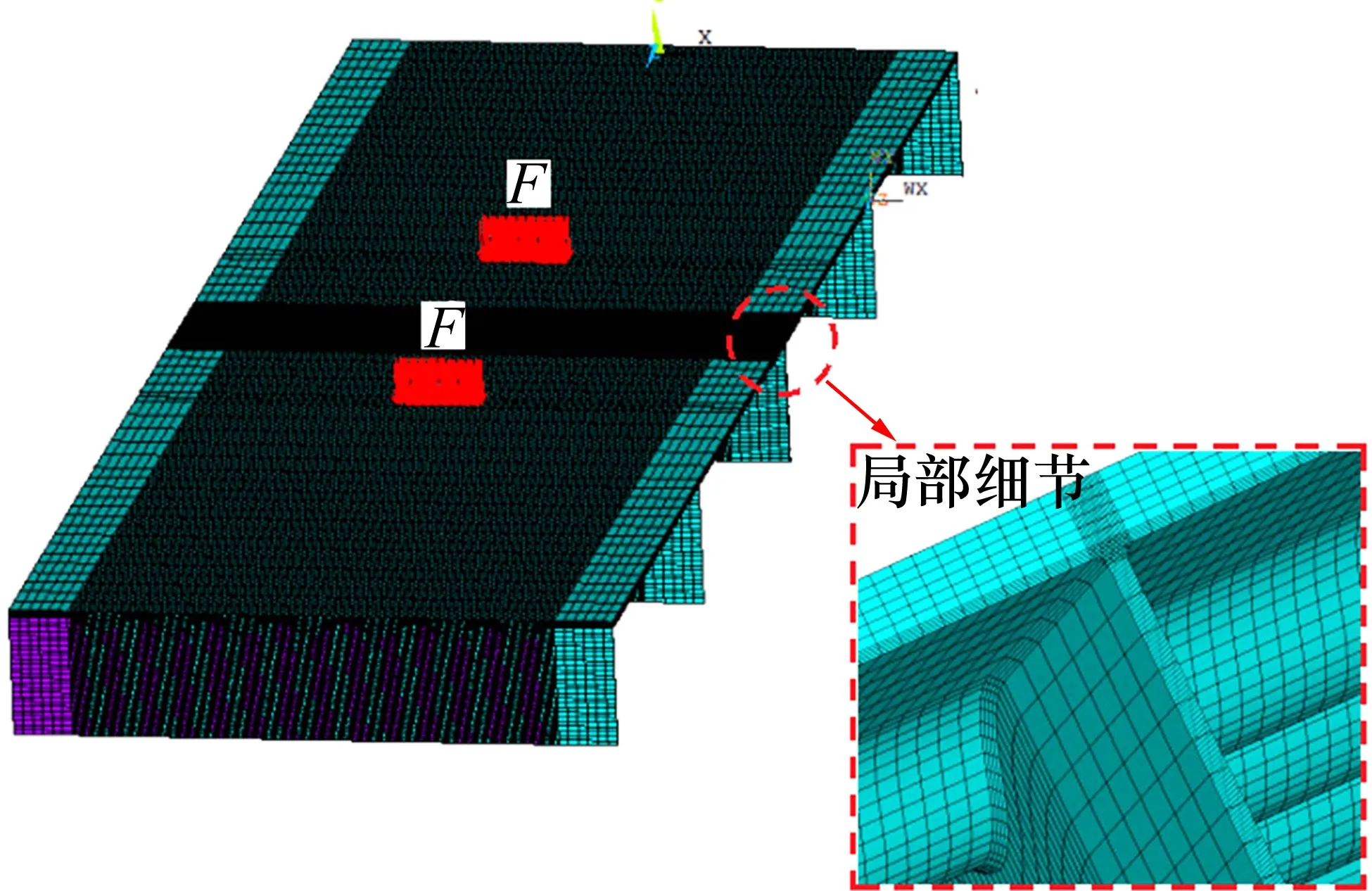
图3 有限元模型Fig.3 Finite element model diagram

参考传统正交异性板及UHPC组合桥面板的研究，取初始截面尺寸为：a=115，b=40，n=2，其变化范围分别为：a取115～140 mm，b取40～70 mm，n取2～7。对模型进行了受力分析。在考虑自重及车辆荷载最不利加载的情况下，分析设计参数变化对结构受力性能的影响。采用控制变量法，分别改变标准曲线的横向投影长度、纵向投影长度及曲线次数，选取如图4 所示的4 个位置对应的应力σ1-σ4作为结构受力性能的考察对象，研究各设计参数的影响规律。其中：σ1为钢板拉应力，σ4为钢板压应力，σ2及σ3均为混凝土拉应力，且应力方向均取结构纵向(Z方向)。各设计参数对结构受力性能的影响结果分别如图5～7 所示。在图5～7 中，拉、压应力均取正值。

从图5～7 中可以看出：①随着a的不断增大，结构各处应力σ1～σ4均呈现出先增大后变小再增大的趋势，并在a=120 mm 附近出现最大值，在a=135 mm 附近出现最小值；混凝土处的应力总变化幅度不超过1 MPa，钢板处的应力总变化幅度不超过3 MPa。表明：a对结构受力性能的影响较小，且存在波动现象。考虑到结构参数的优化设计，将a的取值范围定为最小值附近，即取130～140 mm。②结构各处应力σ1～σ4随b的增大而不断减小，其中，钢板应力σ1及σ4减小幅度明显，应力变化幅度超过10 MPa，混凝土应力σ2及σ3减小幅度不明显，应力变化幅度不超过1 MPa。表明：b对钢板应力影响较大，对混凝土应力影响较小。考虑到增大b会显著增加结构自重，故b取值不能过大，因此，将b取值范围定为55～65 mm。③随着n的增大，结构各处应力σ1～σ4呈不断减小趋势，其中，混凝土应力σ2及σ3变化较小，钢板应力σ1及σ4变化幅度稍大，均未超过3 MPa；钢板应力σ1及σ4随着n的增大变化率逐渐减小，表明：n对结构受力性能影响较小，且随n增大，影响越不明显。同时，随n增大，曲线的最大弯折处的曲率将不断增大，会造成明显的应力集中现象，不利于结构的疲劳性能，因此，将n取值范围定为2～4。所以各设计参数对结构的受力性能都有一定影响，其中，b影响较大，a及n影响相对较小。a,b和n的取值范围分别为130～140 mm,55～65 mm 和2～4。

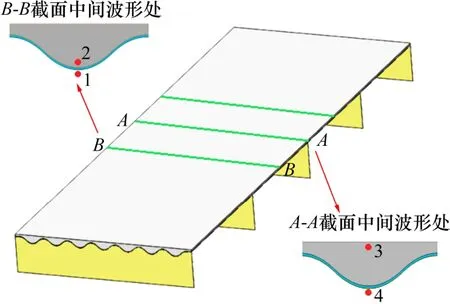
图4 应力关注点的位置Fig.4 Location of interest point of stress

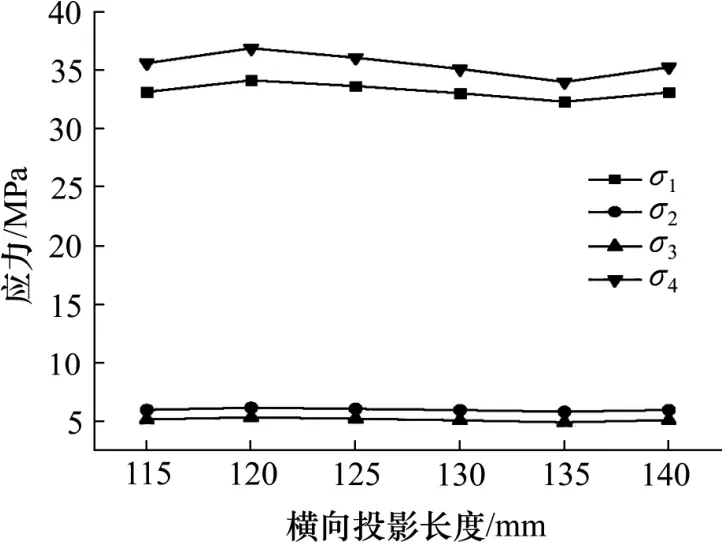
图5 横向投影长度与关注点应力的关系Fig.5 The relationship between the transverse projection length and the stress at the interest point

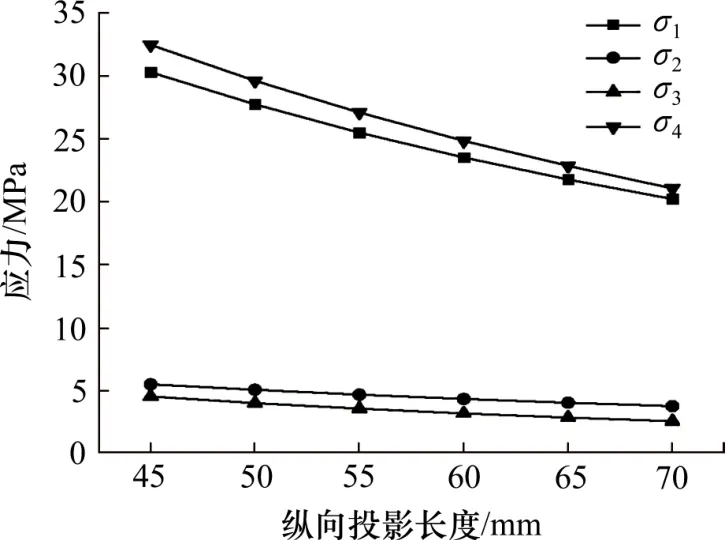
图6 纵向投影长度与关注点应力的关系Fig.6 The relationship between the longitudinal projection length and the stress at the interest point

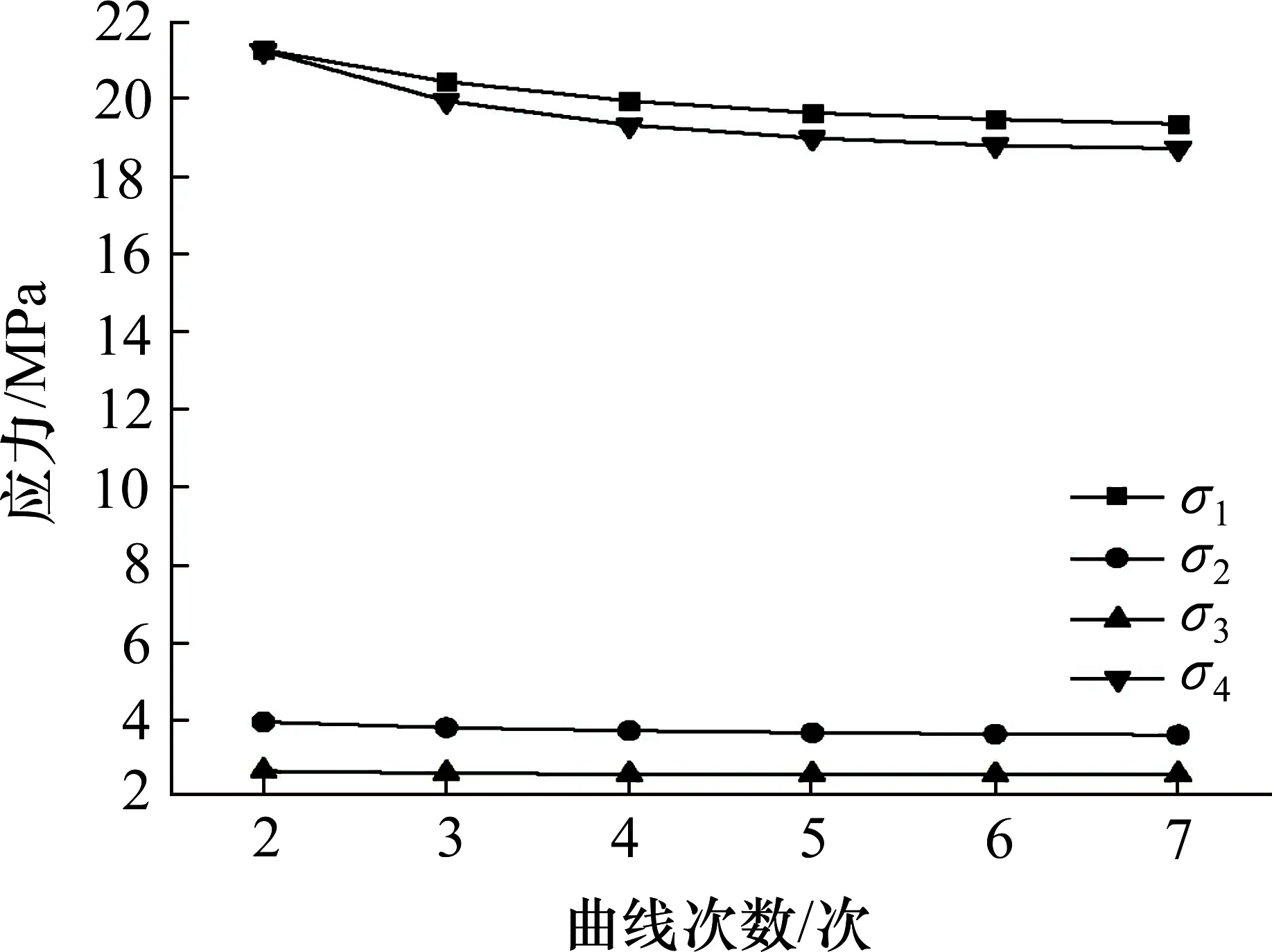
图7 n 曲线次数与关注点应力的关系Fig.7 The relationship between the times of the curve and the stress at the interest point

2 优化设计

2.1 响应面优化设计方案

研究采用Design-Expert 软件与响应面法[11]进行了优化分析。Design-Expert 软件操作方便，三维图形效果直观，在优化分析领域的运用较为广泛。根据各设计参数对结构的力学性能的影响规律分析，确定了各参数的合理取值范围。因此，基于此单因素试验基础上，采用响应面法进行参数优化。利用Design-Expert 软件，采取Box-Behnken 试验设计方案，以a、b、n3 个因素为自变量，考虑到结构的疲劳性能，取结构的疲劳细节控制部位，即跨中横隔板中间波形钢板最低点焊缝处的应力σ0为因变量，进行三因素三水平的响应面试验，中心点重复3 次，共进行15 次试验。在试验设计中，定义a为因素A，b为因素B，n为因素C，最低点焊缝处的应力σ0为响应值Y。试验因素与水平见表1，试验设计方案与结果见表2。

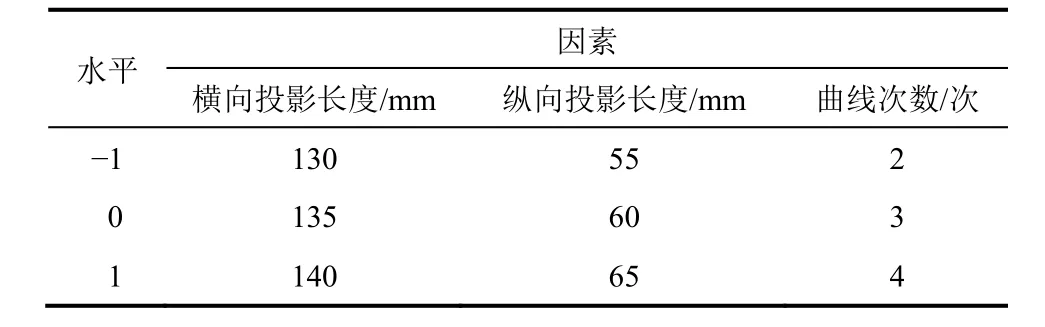
表1 试验因素与水平Table 1 Test factors and levels

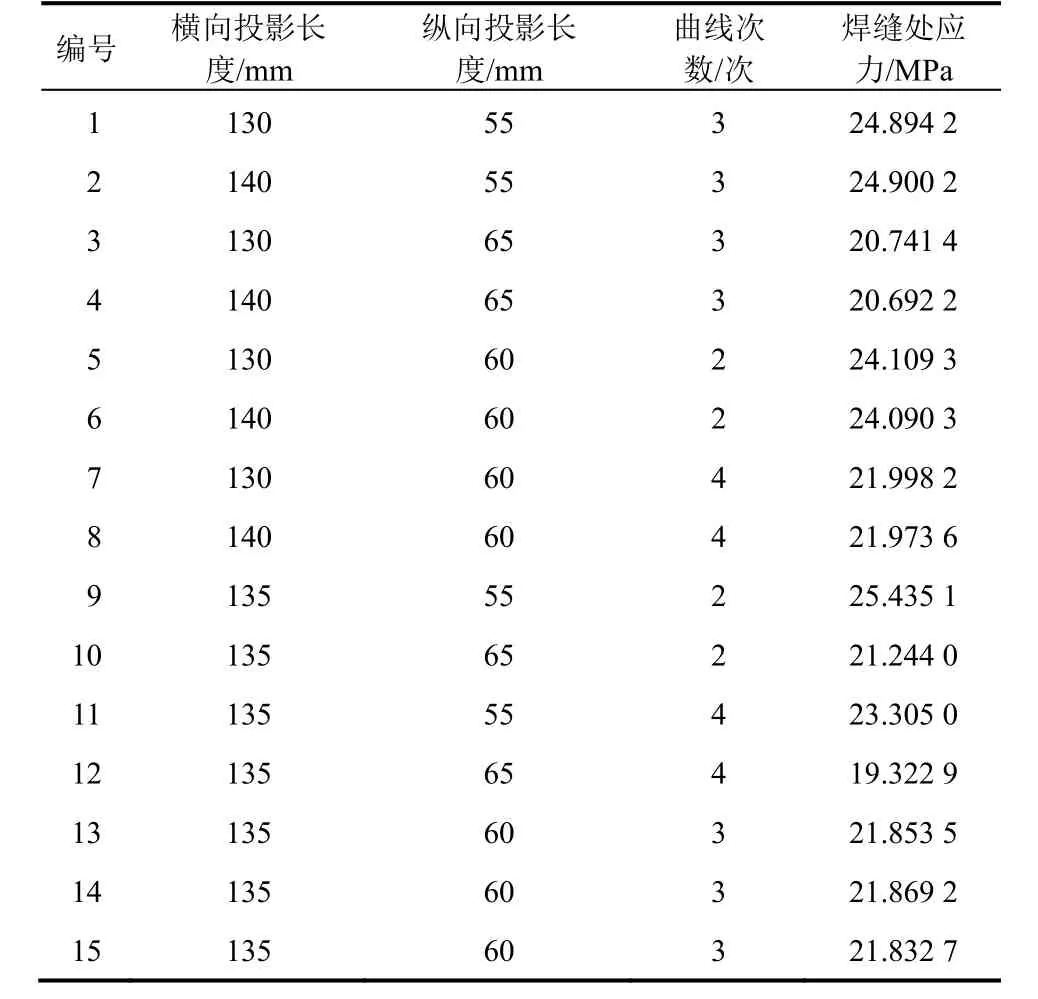
表2 试验设计方案与结果Table 2 Test design scheme and results

2.2 模型的建立与分析

利用Design-Expert8.0.5 软件，对试验结果进行了二次多元回归拟合，得到波形板焊缝处的应力Y与a、b、n3 个因素的多元二次回归模型方程为：Y=21.85-0.011a-2.07b-1.03n-0.014ab-0.001 4an+0.052bn+0.84a2+0.12b2+0.36n2。

从表3 中可以看出，模型P＜0.000 1，达到极显著水平，表明该模型成立。失拟项P=0.110 0＞0.05，故失拟项不显著，表明：回归方程拟合程度较好，该模型可用于分析和预测实验结果。其中，a对波形板焊缝处应力的影响为不显著(P＞0.05)，b与n的影响为极显著(P＜0.000 1)，交互项AB,AC 和BC的影响均不显著(P＞0.05)，表明ab,an和bn、b与n之间对焊缝处应力影响的交互作用不显著。已知模型中影响因素的P值越小，F越大，表明：该因素对响应值的影响越大。从表3 中还可以看出，波形板焊缝处应力影响因素由大到小的主次顺序为：纵向投影长度、曲线次数和横向投影长度。校正决定系数R2为 0.999 8，表明：此模型能够阐述 99.98%的响应值变化。三因素对波形板焊缝处应力的三维响应面结果如图8 所示。

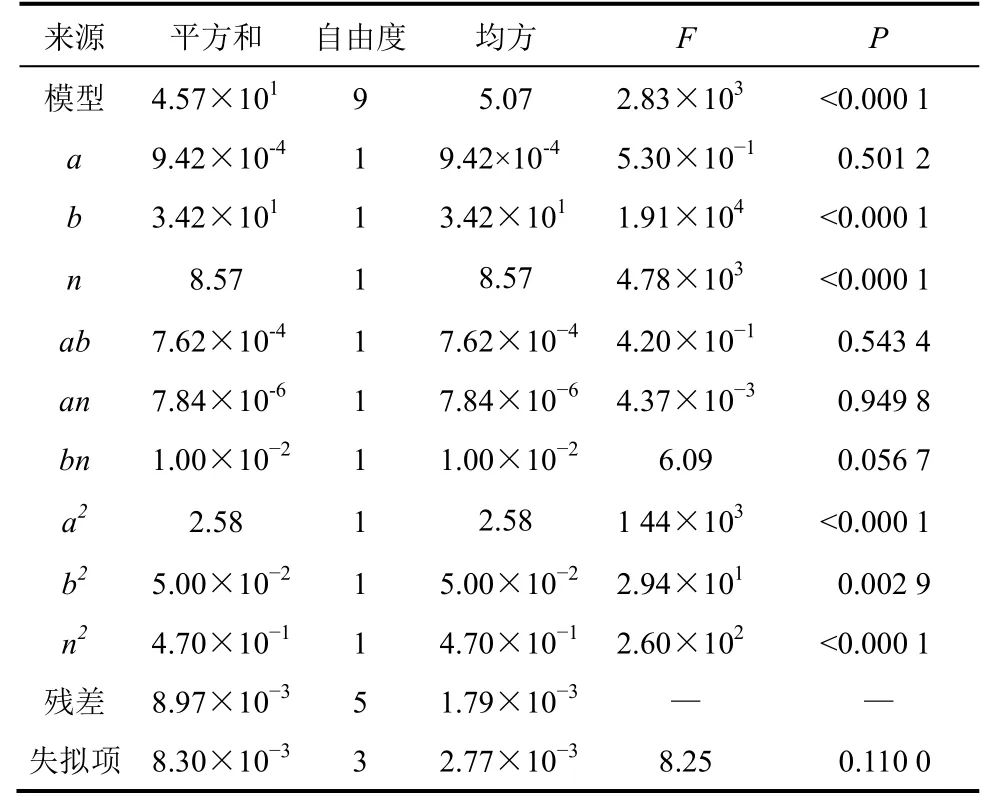
表3 方差分析结果Table 3 Results of ANOVA

2.3 优化结果分析

据优化波形板焊缝处应力的最优设计参数，a为134.95 mm，b为64.97 mm，n为3.9。在此条件下，波形板焊缝处的应力为19.320 1 MPa。为了检验预测结果的可靠性，需要对预测的最优设计参数进行验证。为了实际工程结构应用的方便性与标准化，将最优设计参数修正为横向投影长度135 mm，纵向投影长度65 mm，曲线次数为4。在此最优设计参数条件下利用ANSYS 软件进行了验证试验。有限元模型下波形板焊缝处的应力为19.322 9 MPa，与响应面法预测值19.277 4 MPa 的相对误差为0.236%。表明：验证值与模型预测值吻合较好，优化后的设计参数较为理想。

3 优化后的结构疲劳寿命研究

为研究该结构疲劳性能，分析其可能的易损疲劳细节。对于传统正交异性板，结构应力集中的位置易出现疲劳损伤，如：横隔板弧形开口处，纵肋与横隔板及纵肋与顶板的焊缝连接处。对于本研究提出的全曲线波形板-UHPC 组合桥面板结构而言，由于UHPC 刚度大，在车辆荷载的反复作用下，产生的应力较小，不易出现疲劳开裂；而钢桥面板由于其弹性模量相对较小，且厚度小，刚度较小，更容易出现疲劳裂纹。从单因素试验中的有限元分析可以看出，应力最大位置均出现在钢桥面板处，且位于应力集中最为明显的顶板中间波形最低点。因此，取顶板与横隔板交接位置中间波形最低点的焊缝处为可能的易损疲劳细节(如图9 所示)，以此来考察结构的疲劳性能。

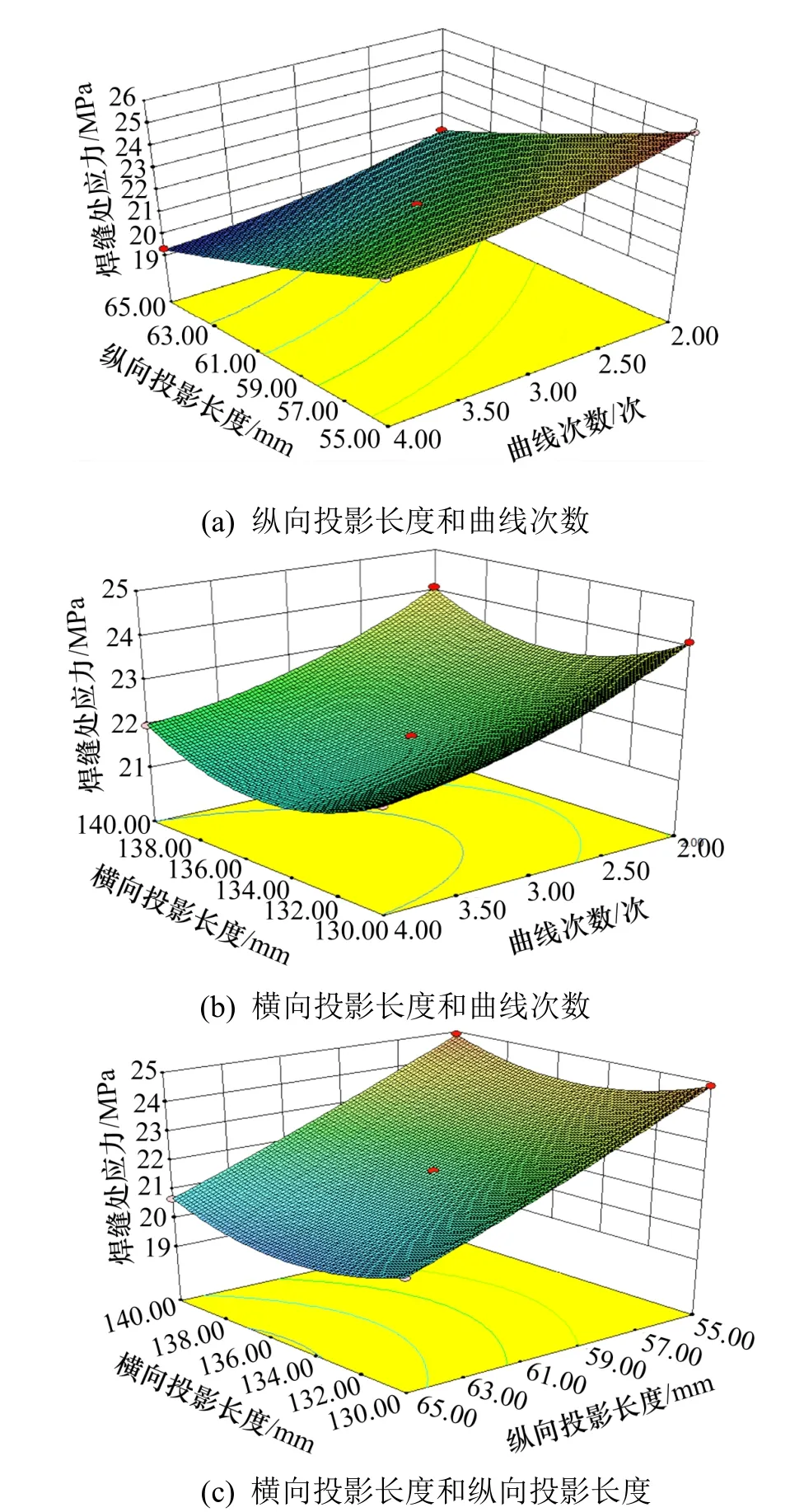
图8 横向投影长度、纵向投影长度和曲线次数对焊缝处应力的三维响应面Fig.8 Three dimensional response surface of transverse projection length, longitudinal projection length and curve times to the stress at the weld

利用ANSYS 软件，建立结构有限元模型。取优化后的设计参数a=135 mm、b=65 mm、n=4，其整体模型尺寸、单元类型、材料参数及边界条件均与单因素试验时相同，钢桥面板在中间横隔板0.5 m范围内的结构为实体单元，其余的结构为板单元，UHPC 与焊缝均为实体单元。根据国际焊接协会(Internation Institute of Welding，简称为IIW)建议的两点线性外推方法，提取疲劳易损细节处焊缝距离焊趾0.4t和1.0t处的主应力，利用外推公式，计算出焊趾处的热点应力。外推公式为：

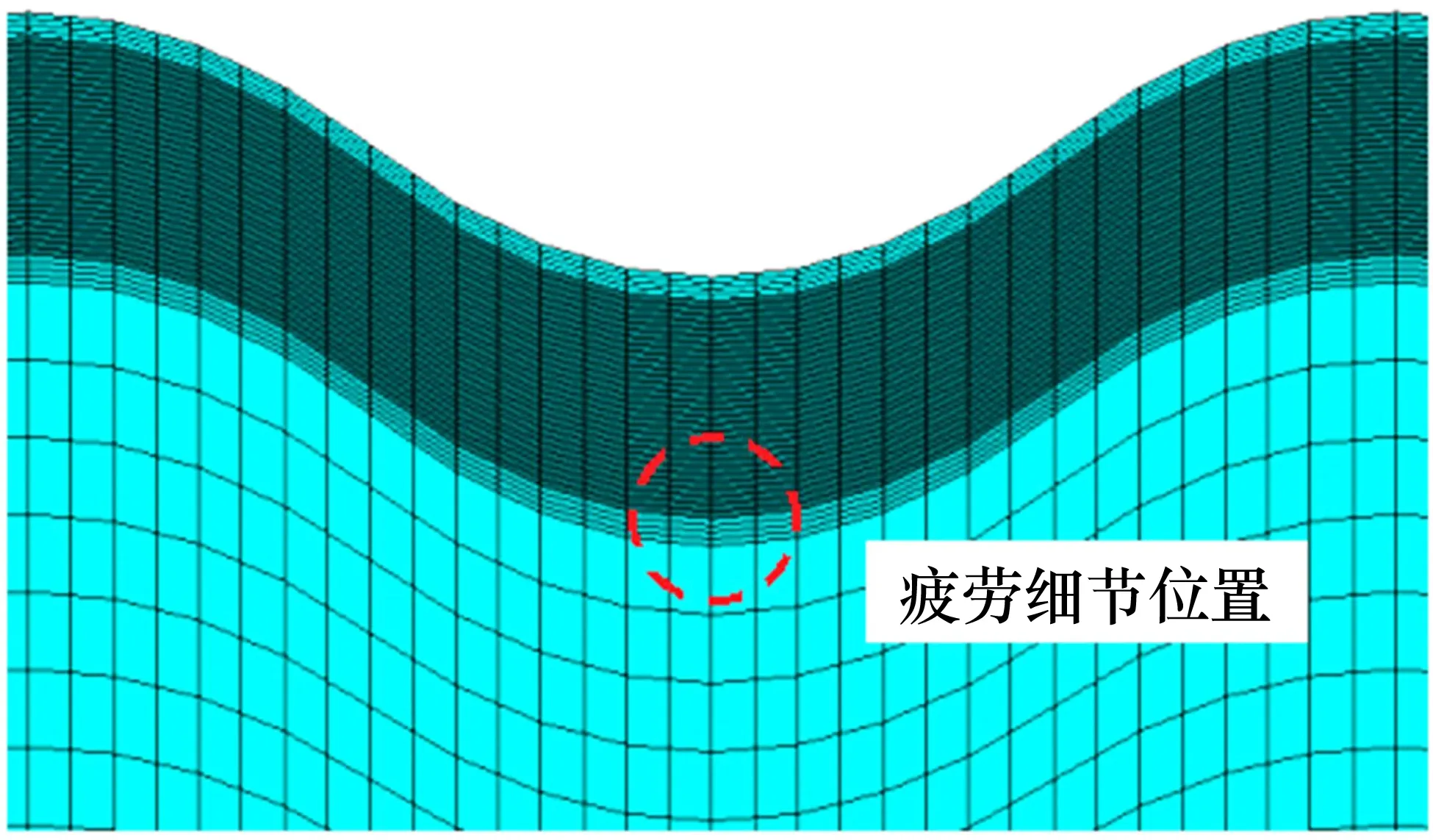
图9 疲劳细节位置Fig.9 Location of fatigue detail

式中：σhs为焊趾处的热点应力；σ0.4t为距焊趾处0.4t处的主应力；σ1.0t为距焊趾处1.0t处的主应力；t为板厚(顶板厚8 mm，横隔板厚14 mm)。

采用Eurocode 中的标准疲劳车辆荷载模型III进行加载。车辆荷载模型为4 轴车，每轴重为120 kN，轮间横向间距为2 m，4 轴纵向间距分别为1.2,6 及 1.2 m。每个车轮的作用面积为 400 mm×400 mm，如图10 所示。取单个轮轴进行横向加载，确定横向最不利位置，共有 24 个工况，疲劳细节处的横向应力历程如图11 所示，得到横向最不利加载位置为x=0.25 m。取一个标准疲劳车，保持横向最不利位置不变，沿纵向进行加载，得到纵向的应力历程如图12 所示。

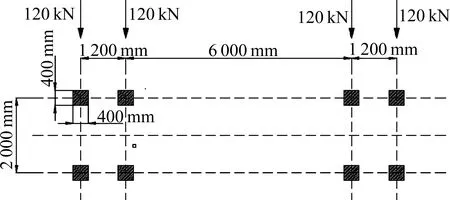
图10 标准疲劳车Fig.10 Standard fatigue load

采用热点应力法，计算结构疲劳强度。取FAT90级S-N曲线来评价焊趾处热点应力的疲劳强度等级。在FAT90 级S-N曲线中，200 万次对应疲劳应力幅为90 MPa，1 000 万次对应常幅疲劳极限为52.63 MPa，10 000 万次对应变幅疲劳截止限为33.2 MPa。偏保守地按重车年通行量取500 000 次。根据纵向应力历程图，利用泄水法，求出应力幅和作用次数，见表4。再根据Miner 线性累积损伤理论，计算结构损伤度[12]。将得到的结构疲劳寿命与传统正交异性板[13]的疲劳寿命进行比较，计算结果见表5。

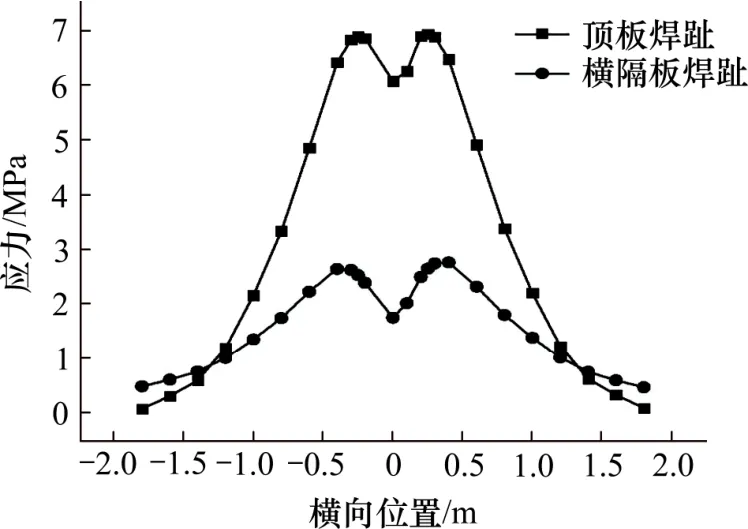
图11 横向应力历程Fig.11 Transverse stress history

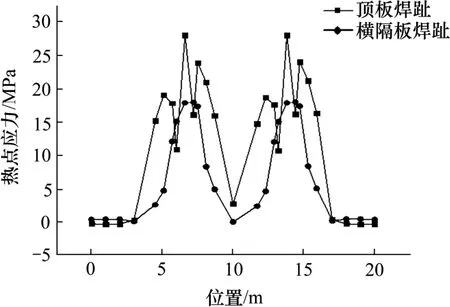
图12 纵向应力历程Fig.12 Longitudinal stress history

表4 应力幅及作用次数Table 4 Stress amplitude and action times

表5 结构损伤度与疲劳寿命Table 5 Structural damage degree and fatigue life

4 结论

为提高正交异性钢桥面板的疲劳性能，提出一种全曲线截面形式的波形板-UHPC 组合桥面板结构。通过有限元法，对其截面设计参数进行了力学性能影响分析及优化，并对其疲劳性能进行了初步研究。得到的结论为：

1) 横向投影长度、纵向投影长度及曲线次数都是影响结构力学性能的重要结构设计参数。其中：纵向投影长度的影响较大，横向投影长度及曲线次数的影响相对较小；纵向投影长度的增大会明显增大结构自重和刚度，曲线次数的增大会增加弯折处的应力集中程度，须合理取值。

2) 利用响应面法，建立回归模型。经显著性和方差分析，拟合程度较好，可用于分析和预测实验结果；3 个设计参数对焊缝处应力影响的交互作用不显著。焊缝处应力影响因素由大到小的主次顺序为：纵向投影长度、曲线次数和横向投影长度。实验值与响应面法预测值误差为0.236%，优化后的设计参数较为理想。

3) 基于热点应力法的结构疲劳性能研究表明，相比于传统正交异性板，优化后的组合桥面板结构的疲劳性能提升明显，顶板焊趾处疲劳寿命提升4.9倍，横隔板焊趾处疲劳寿命接近无限疲劳寿命。