一种基于K-means改进蚁群算法的船舶航线设计方法
马 俊,董良雄,李 军
(浙江海洋大学,浙江 舟山 316022)
船舶航行时必须综合考虑船舶安全性及经济性等因素,根据航行环境(如水深、障碍物等)结合船舶参数,选择恰当的方法设计航线。船舶传统航线是根据个人经验,徒手海图作业方式完成的,但随着船舶日益趋于智能化、自动化、数字化[1],这种方法不仅计算复杂,而且人为因素影响大。因此,许多学者提出各种算法来设计船舶航线,例如Khatib提出人工势场法,易于实时避障和控制,规划的路径较为平滑和安全,但缺乏对全局信息的掌握,易于过早陷入局部最优解,致使出现“死锁”现象。Holland基于进化机制理论构造出的一种隐含并行性随机搜索算法,能够直接通过确定适应度(按照自然进化过程中适者生存和优胜劣汰的原理)作为搜索条件,不受其他辅助信息的限制,但存在运算速度慢、占用储存空间大、出现早熟收敛的缺点。针对上述算法的局限性,M.Dorigo提出一种基于蚂蚁种群觅食的过程来解决复杂路径问题的新型优化算法,即蚁群算法。该方法能提高搜索效率,且具有较强的稳健性和适应性,但蚁群算法受初始参数的影响,容易陷入局部最优解[2]。
因此,本文针对单一蚁群算法在执行过程中存在陷入局部最优解、效率低等问题进行了研究,提出一种基于K-means改进蚁群算法的航线设计方法。即先利用K-means对已标识的栅格海图进行聚类分析,将整个TSP问题分解成许多独立的TSP子问题;然后多次利用蚁群算法对每个子问题求解,并将得到的所有解合并成待求问题的解,该方法能为船舶航迹规划寻找一种更加有效的工具。
1 K-means在海域栅格建模中的应用
K-means是一个对在某些方面相似的数据进行分类组织的过程。航迹规划时,一般要把航行区域栅格化为若干个方格(栅格),然后在航行环境中,对可航区域与不可航区域加以区分,进而设计合理航线。显然,栅格粒度(大小)越细,障碍物划分就越详细,环境模型就越贴近真实环境[3],但往往因为栅格大小划分不同,致使所需时间增加,占用空间大;而且在密集环境下,障碍物往往并不规则,存在与可航区域划分界限不是特别清楚等现象。因此,为了对栅格地图进行更加合理有效分区,可采用K-means方法对栅格进行分区,把代表相似障碍物的栅格聚集到一起,即加快栅格处理时离散化,对栅格进行先分离后集中处理。
本文选取了一个20×20的栅格并采用Python软件进行分簇。先确定簇的个数K,随机生成K个聚类中心点,将数据对象进行分类,即将x个数据对象分成K个簇,使簇间内相似度高,簇与簇之间相似度较低;然后依据簇间数据对象到簇内聚类中心点的距离计算其相似度,根据数据对象到各簇中心点的距离不同,将数据对象划分给不同簇。其Python程序中,当聚类不再变化时,找到最近的聚类中心后更改聚类中心位置,使结果具有可比性、合理性。分簇后得到的结果如图1所示。图1中“箭头”所指的是分簇后该簇的中心点,“数字属性密集程度”代表各对象之间的相似度,其中⓪属性栅格为可航区域,①属性栅格为陆地、岛屿,②属性栅格为浅水区(⓪属性栅格之间能联通,②属性栅格可到⓪属性栅格)。可以看出,海域栅格已被分成了4个集合(簇),每一个集合中都有若干个相似对象,在此基础上为船舶设计路径时,需要考虑的因素大大减少,进而使航迹规划的模型简单化,有助于航迹规划算法精确性的提高。

图1 分簇结果图
同时,海上环境存在着陆地、岛屿和浅水区等不同的通航环境,船舶航行必须避开陆地和岛屿,这是船舶航行设计时的一般原则。此外,船长往往还会根据实际经验设置额外的航线要求,比如安全距离要求,位处浅水区可到可航海域,但可航海域应避免或不能到达浅水区等要求。因此,本文将陆地、岛屿和浅水海域等需要规避的障碍物与可航海域进行了相应区分与标记,并将障碍物进行了一定的膨胀处理,从而满足船舶与障碍物之间的安全距离要求。图2为针对某海图进行栅格化的模型,通过对栅格进行离散化和膨胀化,并对不同栅格属性进行标识,可构建图2中所示的连通关系。

图2 栅格示意连通模型
2 基于K-means改进蚁群算法的设计
2.1 传统蚁群算法的搜索模型
海域栅格建好之后,就可以利用蚁群算法进行最优路径的搜索。蚁群算法作为一种新生仿生启发式算法[4],求解问题速度快,具有并行运算能力及稳健性强等特点,其搜索路径过程如下。
1)分析搜索范围。在如图3所示的栅格图中,某时刻蚂蚁位于图3(a)中黑色圆圈部分,根据所在位置周围其他蚂蚁留下的信息素变化,得到向相邻栅格移动的范围,即向图3(b)的深灰部分移动;最终到达图3(c)的位置。
2)蚁群移动法则。蚂蚁由初始位置向周围栅格i移动,其移动到下一个栅格位置概率为:
(1)
式中,P0→i为蚂蚁由初始栅格0移动到栅格i的概率值;c0→i为蚂蚁由初始栅格0移动到栅格i所经历距离的倒数;b0→i为终点栅格i的信息素浓度;M为蚂蚁移动时可到达的栅格数;B、H为强度系数。
3)实时更新蚁群信息素浓度。蚂蚁在栅格中移动时,根据路径中的信息素浓度进行路径搜索。同时对栅格路径中的信息素浓度进行更新,方法一般采用混合更新策略,计算公式为:
τi=(1-σ)(τi+Δτ) ,
(2)
式中:σ为信息至少挥发系数,σ∈(0,1);τi为原始信息素浓度;Δτ为信息素浓度的变化值。

图3 栅格搜索过程
2.2 基于K-means改进蚁群算法的搜索模型
蚁群算法搜索船舶最优航线时,可运用避让规则、移动法则和信息素实时更新等规则[5]。避让规则简单直观,只需避开障碍物;移动法则为在蚂蚁所处位置的一定范围内选择移动的区域;信息素实时更新规则为根据前一只蚂蚁在所经过路径遗留的信息素选择,信息素越多,代表所经过的蚂蚁数量就越多。
根据基于K-means的航迹规划方案,采用避让规则是比较适合的。因此本文综合考虑障碍物及浅水海域等不可航行因素,并结合航线应用到实际海况中的可行性,在建立的海域栅格图的基础上,利用避让规则进行船舶最优航线设计搜索,搜索过程如图4所示。因传统蚁群算法周围栅格为当前的阴影栅格,见图3(b),使得利用蚁群算法进行船舶最优航线设计搜索后期出现停滞,所以为了加快搜索的速度,采用K-means先对栅格进行聚类并加以区分特性标识,既能保证搜索的精度,又能减少搜索的次数。为了更加明显地看出优势,将数字属性转化为特性栅格,最终得到3种搜索方案并采用方案2进行航行。图4中,黑色栅格(①)属性代表陆地,灰色栅格(①)属性代表岛屿,栅格(②)属性代表浅水区,白色栅格(⓪)代表可航区域,1、2、3代表搜索方案。

图4 K-means改进蚁群算法的搜索路径图
2.3 K-means改进蚁群算法最优航线导航流程
为了对比传统蚁群算法与K-means改进的蚁群算法,本文针对2.1节与2.2节所述的搜索模型进行了航迹规划算法步骤设计与对比。
2.3.1 传统蚁群算法
传统的蚁群算法设计航线时[6],首先对海图进行栅格化,建立栅格模型,在栅格模型中应用转移概率公式(3)和信息素更新公式(4)进行规划航线,重复应用公式(3)和公式(4)直至规划出航线。
(3)
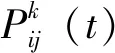

(4)

2.3.2 基于K-means的船舶航线规划方法
基于K-means改进蚁群算法的船舶航线规划方法具体步骤如下。
1)按照前文所述,利用Python算法程序语句先对20×20栅格进行聚类分簇,得到分类后标识其中元素。
2)在类内和类间分别应用2.1搜索模型,对得到的路径进行连接。其中寻找各类的边界栅格路径算法实现如下:①将类内当成一个独立的TSP问题,这样各类内组合就又构成了一个新的TSP。利用传统蚁群算法对其TSP进行求解,得到的最优解就是各类内的最优连接顺序。②求类内与类内间的连接,即类间的连接口。在其中,利用传统蚁群算法求各类间连接口之间的最短路径。③求解新的TSP问题的最短路径,即求得各类间连接口之间的最短路径后,对所有的类,通过①中运算得到的连接顺序把类间连接口连接起来,进而构成了新的TSP问题的最优路径。
3)输出新的TSP问题的最优解。
3 仿真试验结果与分析
仿真平台仍采用前文使用的Python软件,按照海域栅格设计模型方法,对20×20已分类的栅格进行不同标识,并且按要求设置各种海洋环境[7]、安全距离(深度)等参数。为了使仿真结果具有可比性和说服性,参数设置如表1所示。

表1 模型参数设置
利用表1的模型参数进行编程,基于K-means改进的蚁群算法(本文算法)与传统蚁群算法分别设计的船舶最优航线对比如图5所示。从图5可看出,虽然2种算法均有效地避开海上不可航行区域,但基于K-means改进的蚁群算法搜索得到的航线里程更短。该算法设计时要求合理利用浅水区航行,因此航线中不仅保证了船舶的吃水深度,避免重量级船舶行驶至浅水区的搁浅概率,保证所设计的航线航行安全性。
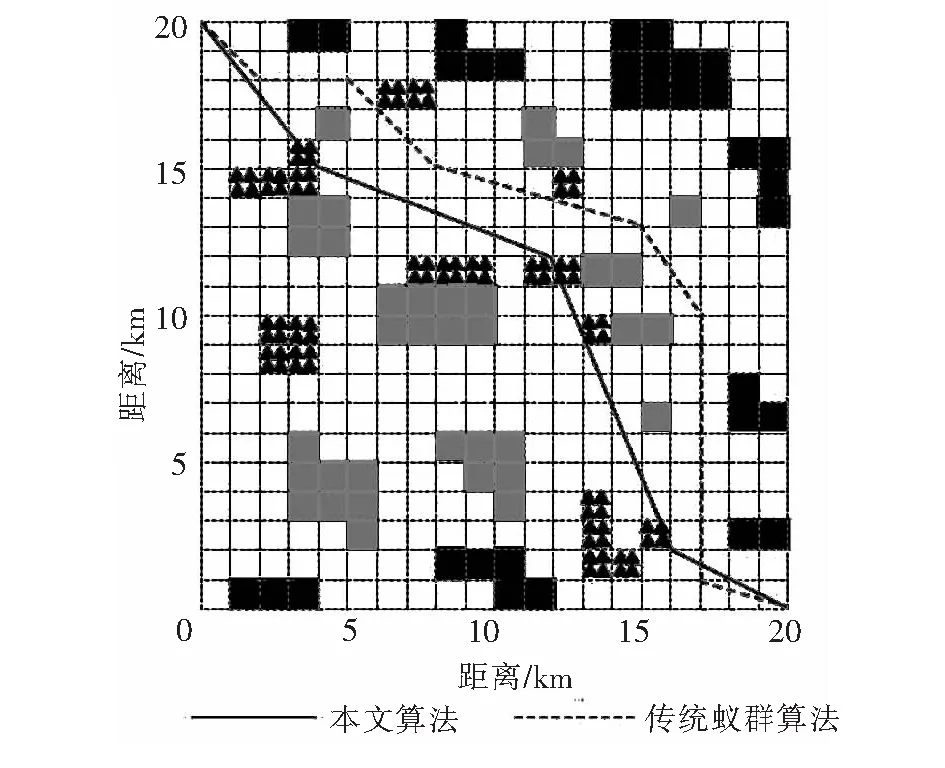
图5 本文算法与传统蚁群算法设计船舶最优航线对比
针对该算法设计生成航线的效率方面,本文共进行5次实验,统计每次实验所耗费的时间,生成航线耗时对比表见表2。不管从单次实验所耗时间,还是从平均所耗时间来看,每次试验所耗时间相比于传统蚁群算法都更少。
4 结束语
本文利用K-means改进蚁群算法设计的船舶航迹规划方法,有效地解决了传统蚁群算法易陷入
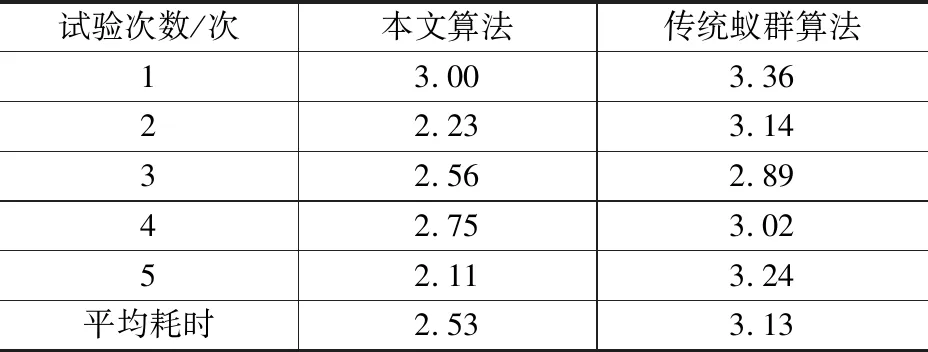
表2 生成航线耗时对比表 s
局部最优解、收敛速度慢等缺陷。通过实验仿真的结果看,本文所提出的基于K-means改进蚁群算法是可行的,该方法能够科学合理地设计出一条里程最短且安全避障,并满足设计时对浅水区的实际需求的航线,算法所耗时间比传统蚁群算法所耗时间更少。

