基于分形理论的天津市住宅价格波动研究

一、前言

房地产业作为国民经济支柱产业之一，其兴衰与宏观经济变动有着密切的关联。房价波动过于频繁，会导致市场发展不协调，资源浪费，企业经营困难，影响经济发展。因此有必要对房价波动特征进行研究，进而提出相关建议以促进城市住宅市场健康、持续的发展。

基于分形理论进行房价波动研究，一些学者从国家角度[1]进行研究，得到中国大陆房地产的分形特征。一些学者则将具体城市[2-3]的房价指数进行实证研究，其中二手房价格分形特征研究最多。但住宅价格包括新房价格及二手房价格，以二手房价格指数为样本，得出的结论不能完整的反应住宅房地产市场价格波动特征。因此，本文以天津市住宅价格指数为研究对象，研究其价格波动特征，以期为住宅房地产市场相关政策的制定提供参考。

二、研究理论与方法

（一）分形理论。分形理论由法国数学家Mandelbrot于1967年创建，用来描述自然界中无法用传统几何描述的缺乏规则的规律。分形的重要特征之一是自相似性。R/S则被认为是最具代表性的分形分析方法之一。在美国的一些经济学家用R/S方法研究了美国股票收益的行为特征之后，该方法被广泛地应用于研究金融领域的时间序列[4]。

（二）重标极差分析法

1.R/S分析法。重标极差分析法（R/S分析法），最初由英国水文学家Hurst提出[5]。后来，此方法通过Mandelbrot[6]得以发展，自此运用在时间序列的分析中，原理如下：

假设有一个时间周期长度为N的时间序列{x(t)}，以长度n（n≥2）划分该时间序列，形成A个子区间Ia（a=1，2，…，A），L为子区间最大长度。记Ia中每一个元素为xi,a（i=1，2，…，n），

求出Ia序列的均值：

对于每个子区间Ia，分别计算标准差SIa、累计均值离差序列{Xt,a}以及极差RIa：

Ia子区间的重标极差即等于Ra/Ia，作为长度n的平均R/S值定义为：

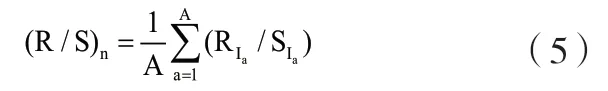
对于不同子区间长度，可得到不同的(R/S)n，可以利用ln(R/S)n与的散点图，用最小二乘法求出的方程斜率即为H指数。

2.赫斯特指数。赫斯特（Hurst）指数的取值范围是[0,1]，利用Hurst指数，可通过如下方法对时间序列进行判别[7]。

H值如果大于0.5且越趋近于1，该时间序列的持久性越强，下一阶段将维持上一阶段的趋势，H值小于0.5则反之。

3.Vn统计量。在对时间序列进行重标极差分析后，如果该序列存在时间的长期记忆性，则可采用Vn统计方法计算出平均循环长度，其计算公式如下：

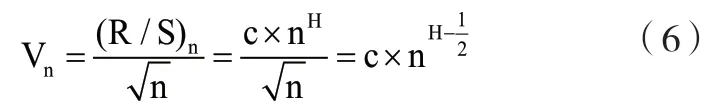
在Vn统计图中，当图形出现了拐点（拐点的出现代表长期记忆过程消失）时，在此形成非循环周期长度。

三、天津市住宅价格波动特征研究

（一）天津市住宅市场现状住及价格指数特征

由天津市新房及二手房价格指数变动情况可知：

1.价格指数总体均持续上涨。2007年4月至2018年11月，天津市新房及二手房价格指数总体上呈上升趋势。其中，新房价格指数在2010年6月-2012年3月及2014年5月-2016年1月略有下降，2017年1月后，进入缓慢平稳增长期。二手房 价格指数大多数处于增长阶段，但在2016年2月-2017年6月，价格指数增长迅速，于2017年6月达到最大值5266，此后逐渐下降。

2.二手房价格指数涨幅更大。二手房价格指数上涨幅度更大，这说明，相对于新房而言，二手房对政府政策导向有着更明显的变化，二手房价格指数变化之大，消费者对二手房市场波动的心理变化较大，不利于二手房市场稳步发展。

（二）指标选取及数据来源

数据来源于中国房地产指数研究院研发布的2007年4月到2018年11月天津市新房及二手房销售价格指数的历史数据。

（三）住宅价格指数重标极差分析

依据上述的方法和数据，运用Matlab9.4.0软件对新房及二手房价格指数时间序列进行分析。经excel软件对上表结果进行线性拟合。图1是新房及二手房价格指数的ln(R/S)n关于ln(n)的拟合图，虚线是其回归线，方程分别为ln(R/S)n=0.778ln(n)-0.5783和ln(R/S)n=0.8657ln(n)-0.6999，R2分别为0.9648和0.972，斜率为赫斯特指数，H分别为0.778和0.8657（见图1）。H值均大于0.5，说明天津新房及二手房价格指数存在较为明显的持久性和分形结构，如果前一个阶段呈上升趋势，在此后阶段房价也将继续上升。

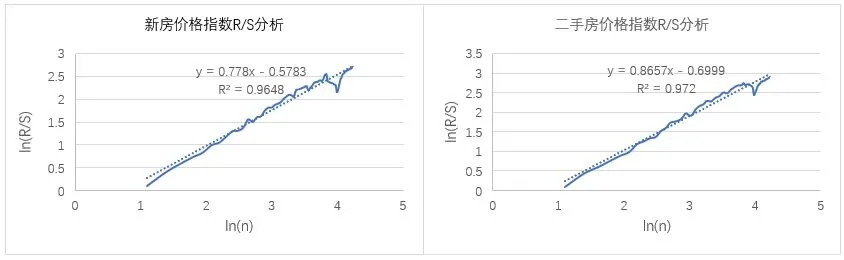
图1 新房及二手房价格指数R/S分析

（四）平均循环长度的计算

作Vn关于ln(n)的散点图，得到图2。

图2 新房价格指数Vn统计量

通过图2可以看出，从图中标示点即为Vn的拐点，在此点之前，图像呈上升趋势，此点后转为下降趋势，确认此点为长期记忆点，此点过后表明时间序列的长期记忆性消失。由ln(n)=3.82864得到n=46，即：天津市新房价格指数序列的平均循环长度为46个月。由ln(n)=3.7612得到n=43，即：天津市二手房价格指数序列的平均循环长度为43个月

四、结论及建议

通过对天津市2007年4月至2018年11月的新房及二手房价格指数的实证分析，可得出以下结论：

（一）天津市住宅价格具有较为明显的分形特征，新房及二手房价格指数的赫斯特指数都大于0.5，即具有状态持久性特征。现在与未来房价指数正相关性很强。

（二）对于天津房价指数，43-46个月为一个循环周期，超过此循环周期，房价变动趋势将发生变化。

这一发现的政策价值在于：

由于房地产市场不能完全依赖经济自发调节，需政府宏观调控，而调控是针对房价进行反向操作的，因此，房价与政策是相互作用的，在进行调控时，需根据房价波动趋势，把握调控时机，以实现房地产业平稳发展。

政策建议：

建立住宅价格监测预警系统，及时跟踪新房及二手房住宅价格指数。在房地产价格波动较大时，应由国家或地方政府制定相应政策以保证住宅价格的平稳运行。密切关注房地产政策实施效果，把握政策调控的最佳时机。