基于SDPM算法的SVM模型的软硬件设计与实现

宋 蒙，蒋生强

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.华为技术有限公司，广东 东莞 523000)

0 引言

支持向量机(Support Vector Machines, SVM)[1-4]是基于概率计算理论的机器学习类算法[5-7]中比较常见的方法。C-支持向量[8]分类应用多以经典的高斯函数为核函数，如何缩短搜寻SVM最优训练参数组合(Optimal Training Parameters Combination, OTPC)的时间一直是近年来学术界研究的热点。

在实际的软件实现中，最经典的得到OTPC的方法是交叉验证训练[9]和网格搜索[10]相融合进行搜索。交叉验证训练需要对训练数据进行折叠处理，处理后再对每组折叠后的数据单独训练；而网格搜索法则需要对每组训练数据进行遍历验证训练。因此这两种方法需要训练的次数较多，延长了得到OTPC的时间。

在传统的硬件实现中，多数情况下都是基于序列最小优化 (Sequential Minimal Optimization, SMO)[11]算法来完成单次交叉验证的训练过程。虽然LIBSVM使用了改进的SMO算法实现交叉验证过程[12-14]，然而改进的SMO算法在搜索工作集索引时，需要计算二阶导数信息，另外还需要计算运算量较大的核函数，这些都使得软件执行交叉验证无法满足实时应用的需求。

为提升SVM搜索OTPC的性能，本文分别从算法和实现两方面进行了探索：首先论证了共享点积矩阵(Share Dot Product Matrix, SDPM)算法[15]，然后进行了硬件实现，并对性能进行了分析和比较。

1 基于SDPM算法的SVM模型

SVM是基于两种数据集的模型。其学习目标是寻找最优的超平面来划分训练数据集。超平面可以用数学方法表示如下：

wTx+b=0。

(1)

SVM基本的思想是找到wT使得分隔是最大的。通过选取合适的核函数K(xi,xj)[15]和惩罚系数C就可以处理非线性的数据，这样原问题就转化为对偶问题：

(2)

典型的高斯核函数为：

(3)

在网格搜索方法的一次迭代中，需要对索引集的数据先进行计算处理，再完成后面的训练，因此以后每次的训练均需要预先处理及后续训练。而SDPM算法先读数据，并对数据进行初始化，将处理后的数据直接存储为点积矩阵，因此后期的迭代过程中不再有中间的初始化及计算过程。故SDPM算法仅需要在搜索之前对点积进行运算再存储到点积矩阵；在之后需要点积向量的搜索过程中，只需统一在点积矩阵中调取向量结果即可。

下面从存储计算量和点积计算量这两方面来分析SDPM算法的复杂度。

(1) 存储计算量

训练数据集的长度为N，点积数据位长为L，存储计算量则为T=W×N2。

(2) 点积计算量

传统方法搜索OTPC过程中点积的计算次数Num1约为：

(4)

式中，m为惩罚系数可选数量，n为高斯核函数参数σ可选数量，s为交叉验证折叠次数，r为迭代平均次数因子。

而使用SDPM算法搜索OTPC时，点积的计算次数Num2为：

(5)

2 软件实现

在SVM构建模型搜索OTPC时，SDPM算法需要将数据集中的参数进行组合，对数据类别精准分类，并对数据折叠处理和交叉验证训练。本文使用了层次设计法：首先，将问题进行简化，将一个大过程分解成几个不同层次的小过程；然后，寻找不同层次之间的衔接和关联，按序进行处理；最后，设置各个不同层次的输入以及输出，实现各个不同层次的功能。

软件设计流程如图1所示。

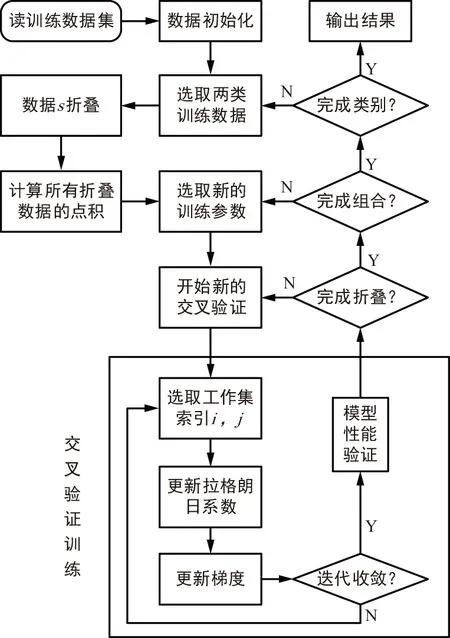
图1 SVM模型的软件实现框图Fig.1 Software realization diagram of SVM model

基于SDPM算法的SVM模型的软件实现分为以下几个步骤:

① 读取数据并对数据进行初始化。

② 训练集中只有两类数据可以直接读取，如果是多类数据，选择两类数据s折叠，折叠后计算并存储点积矩阵。

③ 选取新训练参数并开始新的交叉验证。其中包括更新拉格朗日系数、计算阈值b等。

④ 对训练结果进行汇总，统计数据的准确率。

⑤ 完成②～④后，重新选定训练参数之后运行③和④，将训练集中所有参数组合并全部按此完成训练，得到所有训练的结果。

⑥ 在两类数据训练结束后，从训练数据集中选择其他的两类数据完成③～⑤。训练数据集中所有类别均需如此完成训练。完成训练后将结果保存并输出。

3 硬件实现

虽然SDPM算法利用前期计算并存储点积矩阵的方法减少了点积的计算量。然而软件在建立模型过程中仍然需要涉及大量的计算，无法满足SVM实时应用的要求。本文基于SDPM算法的软硬件协同架构，能在最短时间内搜索出SVM的OTPC，进而完成模型的构建，满足SVM在实时场合应用的需要。本文设计的软硬件协同架构如图2所示。

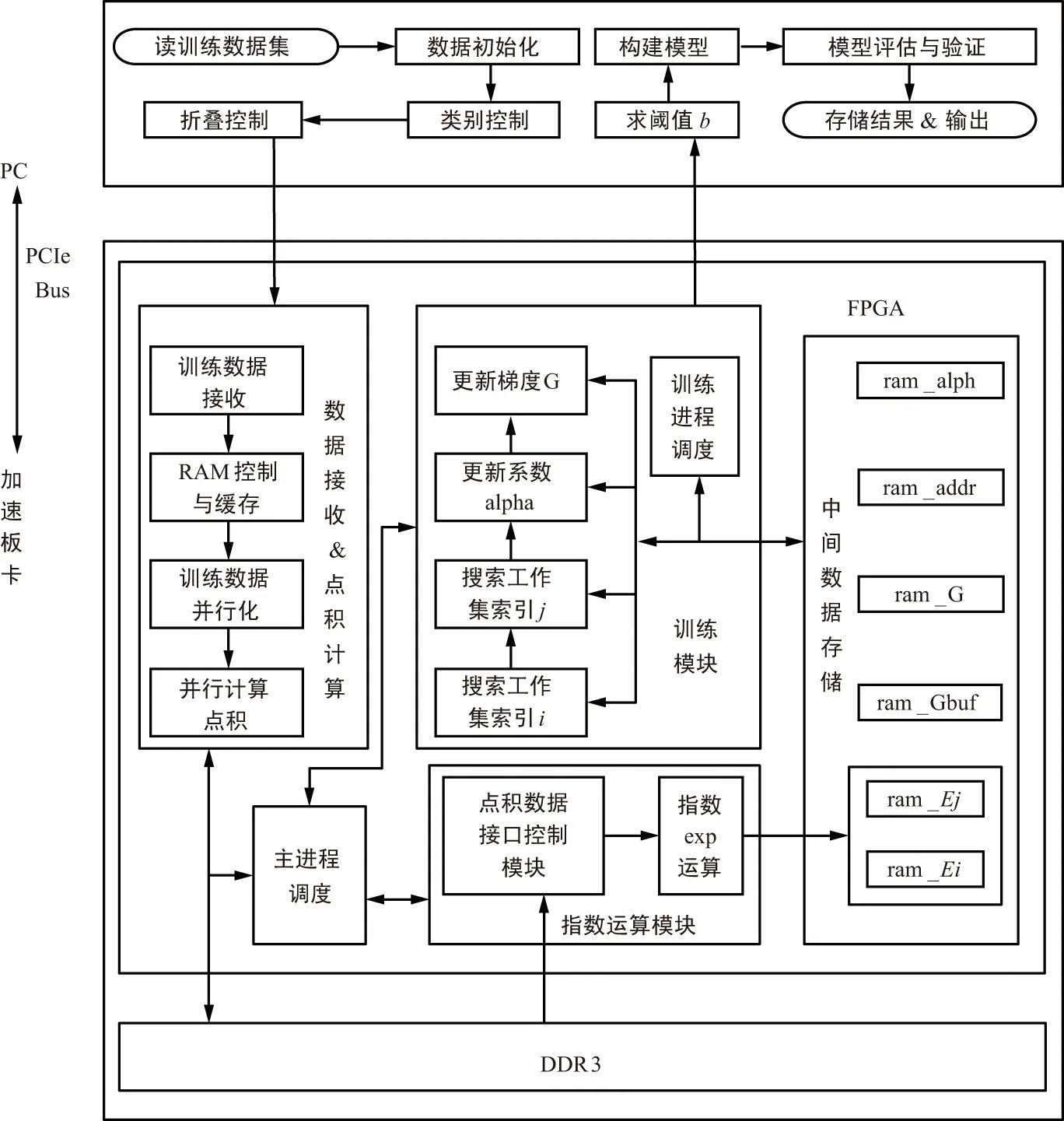
图2 软硬件协同架构Fig.2 Software-hardware collaborative framework

系统整体框架设计如下：硬件系统的结构由PC机、协处理器板卡(加速板卡)和DDR3内存构成。PC机采用X86处理器，加速板卡使用Xilinx的Virtex 7系列FPGA芯片。

系统软件实现如下：硬件上执行浮点运算会耗费大量的资源，且本文对于算法的执行结果，允许一定的精度损失。因此，在使用硬件实现算法时，全部采用定点运算。测试表明，定点运算不会对OTPC造成太大的影响。而硬件的定点化则要求训练数据在输入到FPGA时按定点格式进行编码。

PC机首先读取所有的训练数据集，存储后进行初始化。然后对训练数据集分别进行控制，目的是迅速找到此次需要搜索的OTPC训练数据集，定位训练数据集后进行s折叠并将首次折叠的数据输入FPGA。数据初始化是将所有的训练数据集统一打包成16位的数据，其中1位为符号位，15位为小数位；当训练数据集为多类时，需要先将数据集进行分类，从中取出两类；而训练数据集为两类时，可直接进行训练。

FPGA运算后将一组拉格朗日系数向量回传给PC机，然后PC机求解阈值b，基于b值和系数向量可以构建出模型，并对构建的模型进行评估和验证，在得到全部组合训练参数的准确率后，找到准确率最高的参数组合，以此类推，找到任意两类数据组合的OTPC后输出。

FPGA的内部逻辑模块包括主进程调度、数据接收和点积计算模块、训练模块、指数运算模块和中间数据存储模块5个部分，其中主进程调度模块根据FPGA的时钟信息调度其他功能模块，数据接收和点积计算模块首先是接收定点格式的初始化训练数据，将数据进行点积计算后存储为点积矩阵。训练模块完成搜索工作集索引和更新系数、梯度等交叉训练过程，并将运算结果送达至PC机。指数运算模块从DDR3中读取两路点积向量，最终完成核函数运算并存储至FPGA内部RAM。

4 性能分析和比较

主要对所设计的基于SDPM算法的SVM硬件结构的参数误差、运行时间等方面进行比较。

4.1 参数误差

参数误差是表征LIBSVM和SDPM模型差异的主要参数，参数误差主要包含(a*b)及迭代次数。其中，a*为拉格朗日系数向量，b为模型的阈值。表1～表3分别统计出在数据集Iris(Iris-setosa & Iris-versicolor)，TestD1，TestD2下的LIBSVM和SDPM两种模型的a*参数误差。

表1 Iris下的a*参数误差
Tab.1a*parameter error of cross-validation training in Iris

LIBSVM α 索引LIBSVM α 值SDPM α 索引SDPM α 值索引误差α 值误差15-4.000 0015-4.000 0000464.000 00046-4.000 0000482.598 229482.599 38004.4*10-4821.401 771821.400 62008.2*10-497-4.000 0097-4.000 0000

表2 TestD1下的a*参数误差
Tab.2a*parameter error of cross-validation training in TestD1

LIBSVM α 索引LIBSVM α 值SDPM α 索引SDPM α 值索引误差α 值误差353-0.427 90353-0.429 7604.3*10-33563.116 9503563.118 53005.0*10-4451-2.689 05451-2.688 7601.0*10-4

表3 TestD2下的a*参数误差
Tab.3a*parameter error of cross-validation training in TestD2

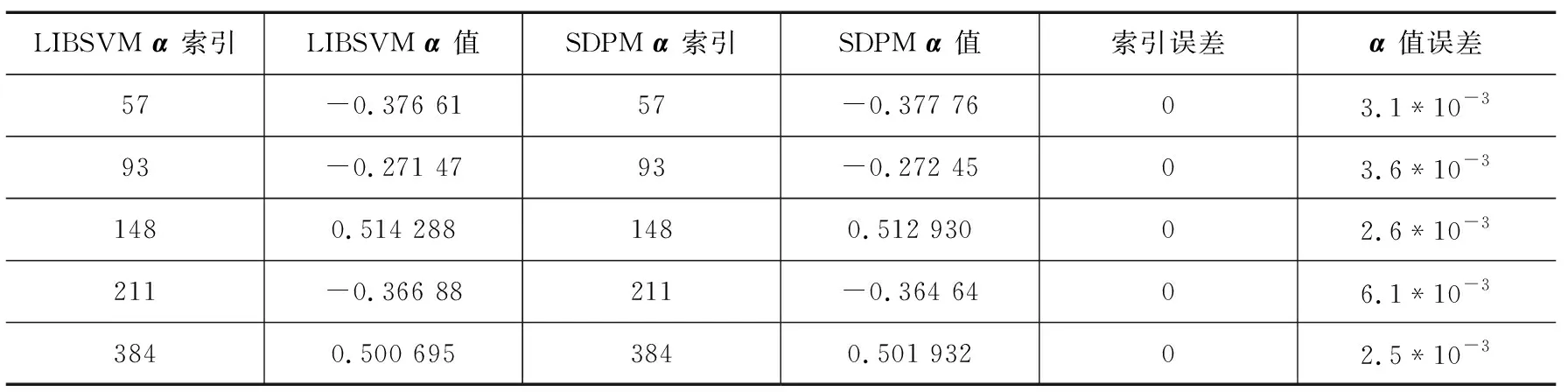
LIBSVM α 索引LIBSVM α 值SDPM α 索引SDPM α 值索引误差α 值误差57-0.376 6157-0.377 7603.1*10-393-0.271 4793-0.272 4503.6*10-31480.514 2881480.512 93002.6*10-3211-0.366 88211-0.364 6406.1*10-33840.500 6953840.501 93202.5*10-3

由表1～表3可知，对于3种不同数据集， SDPM方式训练萃取得到的a*参数索引值和LIBSVM得到的一样， 且a*参数值的误差很小可以忽略不计。SDPM中的中间数据均是归一化后的定点格式，而LIBSVM为全浮点运算，两种方式得到的a*值存在一定的误差，但是由表1～表3可知误差微乎其微，不会造成最终分类结果的误判。表4统计出不同数据集下LIBSVM和SDPM两种模型的阈值和迭代次数。

表4 交叉验证训练的阈值和迭代次数统计
Tab.4 Statistics of threshold and iteration times of cross-validation training

数据集LIBSVM b值LIBSVM迭代次数SDPM b值SDPM迭代次数b值误差迭代次数差异Pendigits0.075 815680.075 9063231.3*10-3-245Iris-0.132 392-0.132 2881.4*10-4-84SPECTF1.049 603241.044 2931915.1*10-3-133TestD10.003 35370.003 20364.5*10-2-30TestD20.002 29110.002 337141.7*10-2+3

由表4可知，数据集为Pendigits，Iris，SPECTF，TestD1时，SDPM的迭代次数远远小于LIBSVM。这大大缩减了模型搜索OTPC的时间，而且b值的误差均小于0.01，并不会对分组造成误判。因此SDPM相对于LIBSVM在不对分组进行误判的情况下，大大减少了训练时间。

4.2 运行时间

表5列出了不同测试数据集下LIBSVM和SDPM的生成模型时长和SDPM的速度提升倍数。由于SVM训练的模型只用了两类数据，因此只选取Pendigits和Iris的测试数据集中第一类和第二类数据用于生成应用模型的时间比较。

表5 生成模型时间对比
Tab.5 Comparison of running time ofcross-validationtraining

数据集LIBSVM时长/msSDPM时长/msSDPM速度提升倍数Pendigits(1&2)3047.441.1Iris(1&2)-0.1-SPECTF462.220.9TestD11243.238.8TestD2782.432.5

由表5可知，SDPM相比于LIBSVM在生成SVM的应用模型时，Pendigits，SPECTF，TestD1，TestD2数据集的提升倍数分别为41.1，20.9，38.8，32.5，而且速度提升的倍数与数据集的长度成正比。在硬件的设计方面也充分考虑了速度提升方法：硬件采用并行架构，较于传统的串行架构可以并行进行处理数据更新；SDPM利用专用的RAM存取中间数据，从而有效减少了训练时间。

5 结束语

目前机器学习和人工智能[16-17]已经深入了各行各业。未来，随着技术的发展还将不断突破目前的计算性能，但随之带来的问题是如何解决机器学习所伴随的超高计算复杂度。本文将共享点积矩阵SDPM算法与机器学习算法SVM模型进行深度融合，利用SDPM算法超低复杂度的实现优势，解决机器学习算法高复杂度的实现难题，并将所提算法进行了硬件实现验证。结果显示，在硬件设计中引入了SDPM算法，减少了训练时间，运行速度提升近30倍，为下一步设计具有超高速、超低功耗、高精度和低复杂度的数字信号处理技术所用的专用芯片提供技术支撑。