光伏电站阵列风荷载数值模拟研究

李 伟，董兆萍，王云浩

（天津城建大学 能源与安全工程学院，天津300384）

大多数光伏电站位于偏远地区，如偏远和人口稀少的地区或工厂屋顶. 为增加发电，太阳能电池板大多是倾斜的，而且角度常与安装地点的纬度相同，因此在经常起风的区域光伏支架阵列容易兜风，如果光伏支架的设计强度和稳定性不能满足当地的风阻要求，昂贵的太阳能电池板极容易被损坏，这将增加光伏电站的维护成本[1-5].

电站组件阵列的布局一般都很规则，风载荷会慢慢衰减，分布并不均匀[6].本文建立了光伏电站组件模型，如图1 所示，并基于仿真软件Fluent6.3[7]，模拟了风速为24.25 m/s 时，电池板在四种不同风向角工况下的受力情况，并对模拟结果进行了分析，旨在为支架的选择提供科学依据.

图1 光伏电站组件模型（10 排）

1 理论基础

本文计算了光伏阵列在强风作用下流场的稳态解，采用基于Favre 平均的N-S 方程求解流场.其数学表达式如下

对于不可压缩流动，密度ρ 不随坐标变化.为确保上述方程封闭，采用（SST）k-w的双方程湍流模型，其中湍动能量k和耗散速率w由方程（4）和（5）决定，即

式中：F1为调配函数；vt为湍流涡黏性系数；由式（6）确定，即

详细的模型求解过程见文献[8].

给定风速等相关参数，通过求解流体方程，得到流场稳态解.根据光伏阵列壁面上的压力分布，可得到其稳态的风荷载特征.

2 数值模拟

2.1 几何模型

本文计算中，光伏电站组件安装在具有一定坡度（约为3.9°）的山坡上. 山坡长203.9 m，宽300 m，高13.11 m，山坡前入口长30 m，此即计算域的尺寸.计算域示意图如图2 所示.电池元件模型的入口与侧面和边缘之间的距离，顶部和电池元件模型之间的距离，并且计算域退出与模型之间的距离都大于模型高度的5 倍.组件尺寸172 m×9.9 m×0.1 m（长×高×厚），竖向1 列10 行排列，与地面的安装倾角为20°. 几何模型按照实际尺寸建立.

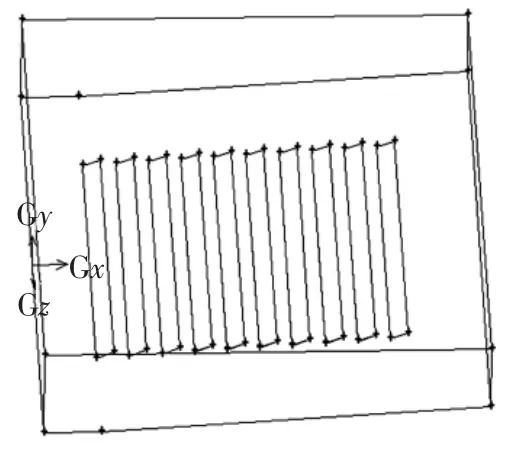
图2 计算域及模型示意

2.2 网格划分

本文采用四面体网格来划分计算域的空间[9]. 由于光伏阵列的长宽和厚度比值过大，直接进行网格划分非常困难，因此采取分块划分网格的形式.在电池组件附近的网格加密，并以一定的渐变率向四周发散，电池组件周围的空间网格节点是密集的，远离电池组件位置网格逐渐稀疏.整个计算域的网格划分如图3 所示，网格总数为300 多万.

图3 计算域网格划分

2.3 模型设置

本文利用Fluent6.3 的计算平台对铜川大型光伏电站的风荷载问题进行数值模拟，模拟过程采用k-ε湍流模型，基于压力的隐式解算器，SIMPLE 算法，用于求解方程.动量方程及模型方程中对流项选用QUICK格式离散，动量方程二阶差分.

2.4 边界条件

数值模拟中，模拟模型的风场边界条件为：底面为壁边界，设壁表面粗糙高度为0.05 m.侧面及顶面为壁面边界.入口使用速度入口，入口风速24.25 m/s，出口为充分发展流.模型表面为无滑移壁面.

3 计算结果分析

3.1 不同风向组件表面风压特性

3.1.1 0°风向角

0°正向风时的组件上表面为迎风面，下表面为背风面.上、下表面压力之差便是单位面积组件所受的风荷载.0°和45°风为正向风，组件承受的是下压力.

0°正向风工况下，除了个别组件的小部分区域，每个组件的上、下表面的风压是沿长度方向对称分布的，如图4 所示，这与事实相符，说明数值模拟是合理的.

图4 正向风（0°）工况电池组件上下表面压力分布云图

整个光伏阵列风压分布规律是组件中间部分压力分布均匀，两侧则差别较大，这说明两侧受风影响较大，下表面两侧的压力明显低于其中间部分，说明组件两侧承受的风荷载较大.第一排组件的上表面承受最大风压，特别是上表面的下半部分，而其下表面的压力较小，上下表面压差很大，所以第一排组件所受的风载荷最大，特别是其下半部分. 第二排组件上表面受到的压力较小，下表面的压力在所有组件中最大，上下表面压差很小，所以第二排组件所受的风荷载最小，且其受力比较均匀.

3.1.2 45°风向角

45°风向角的风压如图5 所示，对于45°风向，组件上、下表面的最大风压值出现在风的入口处，风压值沿着组件长度方向不断降低；由第一排到第十排的上、下表面的风压值为递减趋势；沿着45°线方向，组件上、下表面受到的风压呈现降低的趋势；综合看组件受力最大的位置在第一排组件的迎风端.

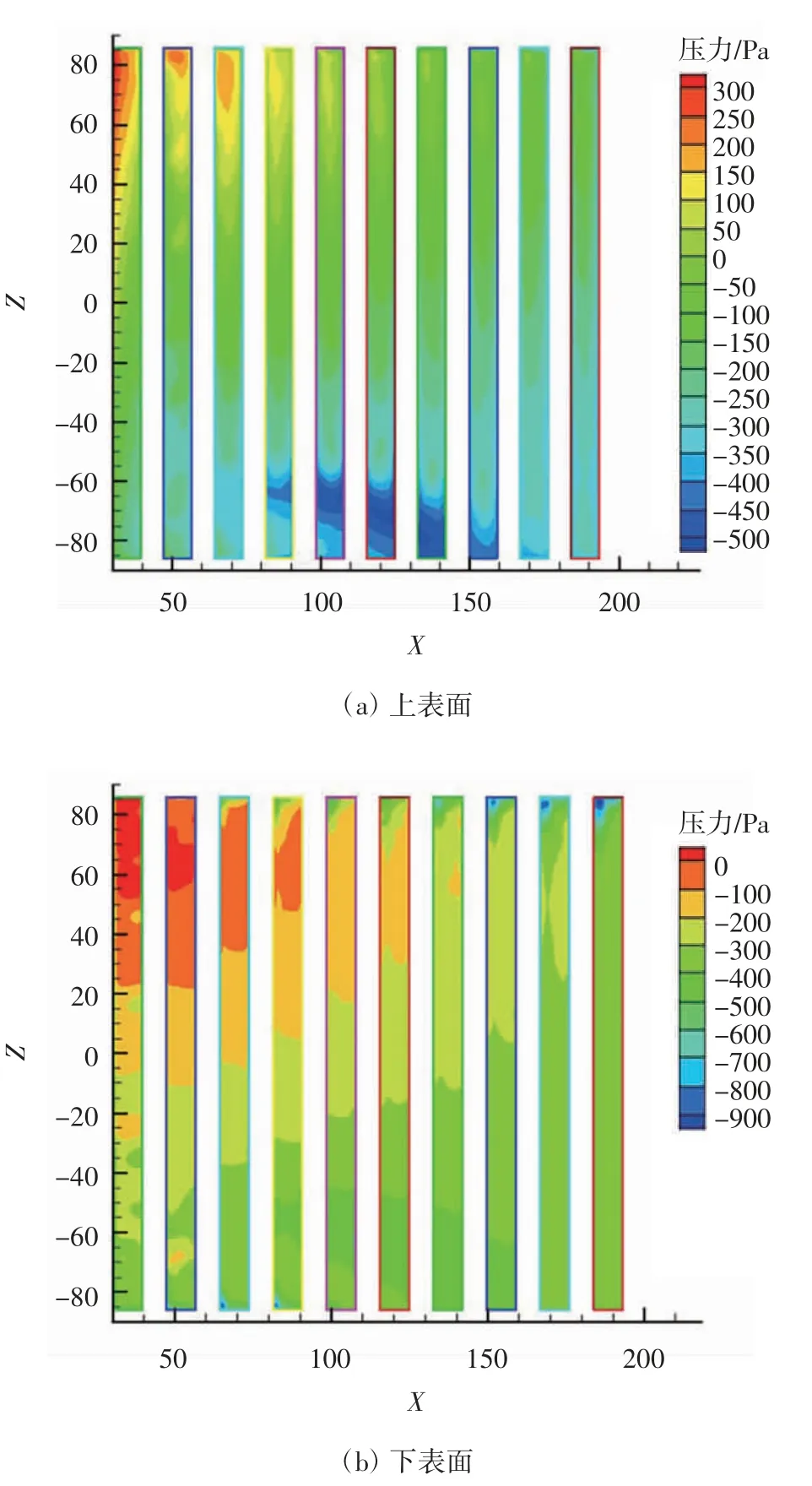
图5 正斜向风（45°）工况电池组件上下表面压力分布云图

3.1.3 135°风向角

当135°风和180°风是逆风时，下表面压力大于上表面，组件承受的是掀起力.对比45°风向图，135°风向图下表面风压分布规律和45°风的上表面风压分布规律很相似；而上表面和45°风时的下表面相似，如图6 所示.所以每排组件的迎风侧受力更大；受力最大的是首先迎风的第10 排组件.

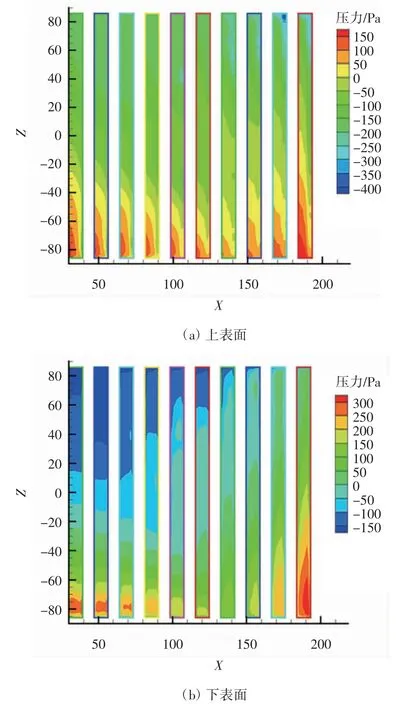
图6 逆斜向风（135°）工况电池组件上下表面压力分布云图

3.1.4 180°风向角

从180°逆向风的风压图中可以看到每个组件上、下表面的风压基本上都是沿着组件长度方向对称分布，其对称度比0°风时略差.这是因为逆向风时风的湍流度增大，不确定性因素增加.

对比0°和180°风压图，可以发现180°风时组件下表面的压力分布规律和0°风的压力分布规律非常相似，如图7 所示.都是组件两侧压力大，中间压力小.

180°风时第十排组件上、下表面的压差最大，其所承受的压力相应也最大.与0°风时的第一排组件受力位置不同，180°风时第十排组件主要受力位置是其中上部分.

3.2 光伏阵列风载荷计算

根据参考动压对壁面压力进行归一化处理，可以求得光伏阵列无量纲压力系数，即

式中：P为光伏阵列壁面压力；ρ 为空气密度；v¯表示风速.

规定迎风面与背风面压力系数的差值等于净压力系数，则其时间历程CJ（t）可由下式得到，即

式中：下标J 表示净压力，下标M 表示迎风面，下标N表示背风面.

对式（8）进行面积分可得

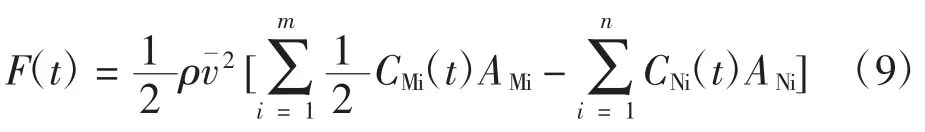
式中：F（t）为垂直壁面方向的总净力；m、n表示迎风面、背风面上网格数量，AMi、ANi表示壁面单元面积.

将F（t）转化为如下无量纲形式式中：B和L代表光伏板的宽度和长度.

净力系数CF（t）的变化趋势可以表征光伏结构设计关键因素风载荷的变化趋势.

图8 给出了0°正向风、45°正斜向风、135°逆斜向风、180°逆向风四个不同风向情况下各组件的风荷载净力系数曲线，净力系数的具体数据在表1 中列出.

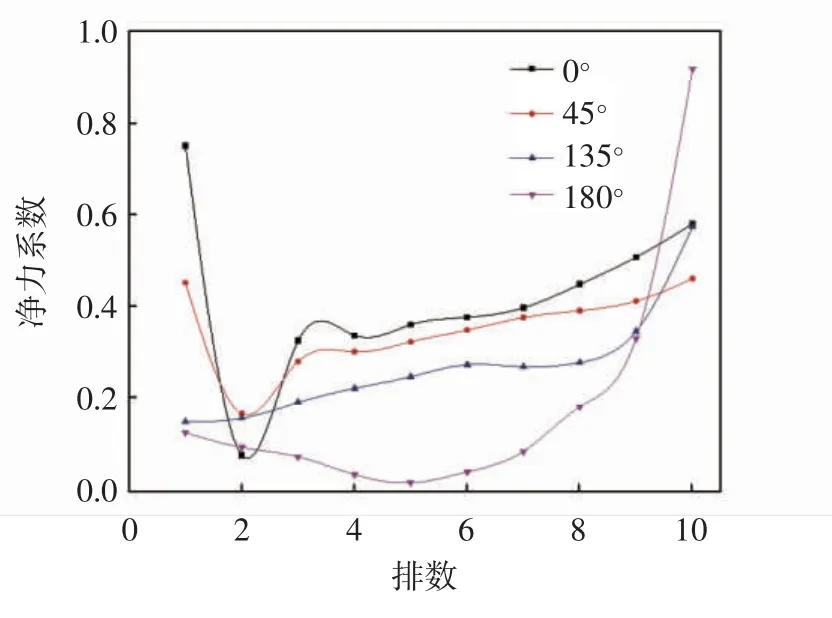
图8 四种风向下各排组件风荷载净力系数曲线

表1 不同风向时各排组件风荷载净力系数

如图8 所示，在四种风况下，最大风荷载都是由首先受风的那排组件承担.即正向风时最大风荷载出现在第一排组件，逆向风时最大风荷载出现在第十排.

对比图8 中四条曲线发现0°正向风和180°逆向风两种工况下其组件的最大风荷载（C（Ft）分别为0.750 384、0.917 342）要高于45°和135°风向两种工况下其组件的最大风负荷（C（Ft）分别为0.461 76、0.574 107）.

对比四条曲线可以看到，整个光伏阵列的最大风荷载出现在180°逆向风工况的第十排，风荷载C（Ft）为0.917 342.以此最大荷载为标准，各排组件所受的最大风荷载与整个光伏阵列的最大风荷载的比值如图9 所示，这在光伏支架构件结构设计时是一个重要的参考标准，具体数据在表2 中列出.

图9 各排组件最大风荷载与光伏阵列最大风荷载比值

表2 各排光伏组件最大风荷载与第十排最大风荷载比值

值得注意的是，图9 和表2 显示第二排组件承受风荷载很小，仅为第十排最大风荷载的18%. 经过分析认为，原因是本研究中组件很长（172 m），长、高比很大，第一排组件阻挡风的作用对第二排影响非常大，所以第二排组件受力非常小. 虽然计算结果显示第二排承受风荷载很小，但在实际工程中建议第二排按照第三排的最大风荷载甚至更大一些进行设计，以免发生第一排组件受损的状况.

4 结 论

通过对一列十排的光伏阵列（模型1）风荷载进行数值模拟研究，得出以下主要结论.

（1）阵列首尾两排（第一和第十排）组件所受的风荷载最大，第二排到第九排所受风荷载逐渐增大，第二排所受风荷载仅为第十排最大风荷载的18%，第九排所受风荷载为第十排最大风荷载的60%.

（2）第一排主要受力位置为组件下半部分，第十排主要受力位置为其中上部分.各排组件长度方向的两端承受风荷载较大，中间位置风荷载较小.

（3）在实际设计中，可选择最外侧阵列为设计标准，中间阵列根据荷载情况，通过光伏阵列布局优化，可节省设备成本.