考虑测试可靠度的诊断策略优化方法∗

叶 文 吕鑫燚 吕晓峰 马 羚

（1.国防大学联合勤务学院 北京 100858）（2.海军航空大学青岛校区 青岛 266041）

（3.西北工业大学电子信息学院 西安 710072）（4.海军航空大学 烟台 264001）

1 引言

诊断策略优化是测试性设计工作的重要组成部分，其目的是为系统设计一组最优诊断策略，即设计的测试序列满足系统要求的测试性指标，同时该序列的测试代价尽可能低［1］。目前已有的诊断策略优化方法一般都假设测试是可靠检测即测试不会产生虚警和漏检［2～5］，而这在实际中往往是不成立的。并且在工程实际中，测试过程中可能出现的错误会随着系统复杂度的增加而增加，错误诊断带来的额外开支往往超过了测试成本［6］，因而诊断策略优化过程中不能忽略测试可靠度的影响。

文献［7］首次提出了不可靠测试的概念。文献［8］研究了基于不可靠测试的诊断策略优化方法，但没有考虑虚警问题。文献［6］将测试可靠性参数转化为误诊、漏诊费用，但用于生成诊断策略的不确定AO*算法计算过于繁琐。

针对上述问题，本文首先从平衡测试可靠度，测试代价与检测性能之间矛盾的角度出发，将测试可靠度相关指标引入诊断策略优化模型中，以提高构建模型和诊断策略优化结果的有效性和可靠性。然后，在经典信息熵算法的基础上，设计了相应的改进准深度算法进行诊断策略优化选择。最后通过实例验证和分析本文方法的效果。

2 问题描述与建模

2.1 优化模型的建立

本文假设单故障发生且各故障相互独立，诊断策略优化问题主要由以下几部分组成［9～11］：

1）F={f0,f1,…,fm}表征m+1维的系统故障状态集，f0表示系统无故障状态，fi(1≤i≤m)则表示m个潜在故障状态中的一个故障状态；

2）P={p0,p1,…,pm}表征对应m+1个系统故障状态的概率集合；

3）T={t1,t2,…,tn}表征n维的系统备选测试集合，C={c1,c2,…,cn}表征对应n个测试的测试代价集合；

诊断策略优化的目标是基于上述系统参数设计一组测试序列组成诊断树Ds，以最小的测试代价实现对系统中所有故障状态的检测与隔离。期望测试代价［10］可通过式（2）进行计算。

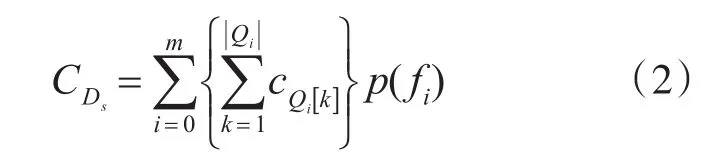
式中：Qi表示隔离故障fi所用的测试集合，|Qi|表示该测试集合的容量，cQi[k]表示Qi中第k个测试的费用，p(fi)表示故障fi的概率。

2.2 测试可靠度分析

目前已有的诊断策略优化方法一般都假设测试是可靠检测即其能以100%的概率对相应的故障进行正确检测，而这在实际中往往是不成立的。在实际电子装备中，每个测试信号都是由传感器进行测量，由于传感器自身可靠性（故障率）、环境因素的影响、电磁干扰及固有的测量误差等因素综合作用，测试可能会发生虚警或漏检，进而对诊断策略优化结果的准确性和可靠性产生严重影响。因此，如何平衡测试可靠度，测试代价与检测性能之间的矛盾，建立更加符合工程实际的诊断策略优化模型便是提升诊断策略优化方法性能亟待解决的关键问题。

针对上述问题，本文考虑在原有诊断策略优化模型的基础上增加工程实际中的测试可靠性需求，对测试可靠度定义进行总结并拓展为诊断树可靠度，并在诊断策略优化模型的建立过程中将诊断树可靠度作为一项优化目标，有指向性地对测试进行选择，使得优化结果在工程上满足检测性能和测试可靠性需求同时尽可能降低期望测试代价。

测试可靠度，即在规定的条件和规定的时间内，该测试正确检测到故障发生的概率。其取值与传感器的可靠性（故障率）、信噪比、灵敏度以及应用环境因素有关。为了定量计算测试可靠度，引入测试概率集Pτ［6］，用以表征测试的不可靠性。

式中：pdij和pfij分别表示tj对fi的检测概率与虚警概率。

本文测试可靠度主要由测试概率集以及故障与测试的相关关系计算得到，如式（4）所示。

假设诊断策略优化选择的测试序列组成诊断树Ds，则诊断树可靠度可表述为

式中：rQi[k]表示测试序列|Qi|中第k个测试的测试可靠度。

综上所述，建立考虑测试可靠度的诊断策略优化模型如下：

3 考虑测试可靠度的诊断策略

信息熵算法是一种用于求解诊断策略优化问题常用的启发式搜索算法［12］，其对于求解一定集合规模的诊断策略优化问题具有良好的性能，但是随着集合规模的增大，则只能得到局部最优解。因为该问题是一个组合优化问题［13］，求解难度随系统规模加大而成倍增加。而准深度算法是一种建立在信息熵算法基础上的，并能有效求解组合优化问题的计算方法［14］。因此本文利用其可改善信息熵算法的特点，对基于信息熵算法的测试可靠度诊断策略进行改进，设计一种基于改进准深度算法的测试可靠度诊断策略。

3.1 基于信息熵算法的测试可靠度诊断策略

设系统的故障集为F，备选测试集T中的测试点tj执行之后，将F分为测试tj通过（Pass）子集Fjp和测试tj不通过（Fail）子集Fjf，其概率可由式（7）、（8）计算得到。

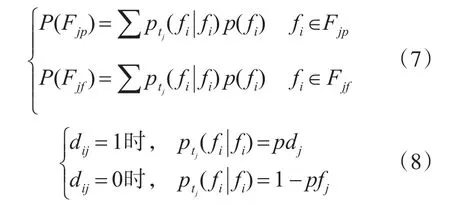
根据信息理论，测试点tj提供的关于故障集F的信息量为

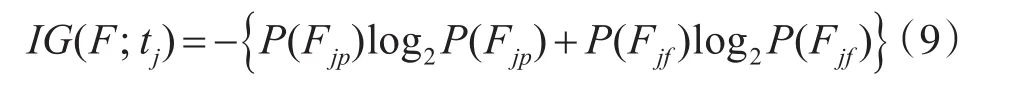
综合考虑测试点信息量、可靠度和测试费用的影响，设计启发式函数如下：

基于信息熵算法的测试可靠度诊断策略优化的目标是为系统选择一组测试序列生成故障诊断树，使系统中所有故障状态都能被检测与隔离，同时满足各测试点信息量、测试可靠度与测试代价比值最大。

具体的计算步骤如下：

1）设待测系统的初始故障状态集和初始测试集分别为x=F和t=T；

2）测试集t中每个测试tj将故障状态集x划分的子集xjp和xjf，根据式（3）计算其概率p(xjp)和p(xjf)；

3）根据式（6）从测试集t中选择一个启发函数值最大的测试ts；

4）测试ts将故障状态集x划分为xsp和xsf两个子集，用式（11）更新各个子集中的故障概率：

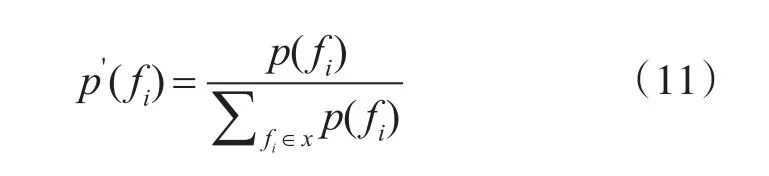
5）将t更新为原测试集删除ts后的测试集，x更新为步骤4）中产生的各个故障子集，重复执行步骤2）～5），直至各故障子集中不多于一个元素。

3.2 基于改进准深度算法的测试可靠度诊断策略

准深度算法是建立在信息熵算法基础上的一种一步前向回溯算法［15］。该方法的基本思路为：采用两个步骤分别从测试层面和诊断树层面确定一个测试。首先在测试层面，用信息熵算法构造出以各候选测试为顶点的临时诊断树。而后在诊断树层面，用启发函数评价和选择这些临时诊断树，得到最佳诊断树。将该诊断树的第一个测试作为当前最佳测试。为了提高测试可靠度对测试序列生成的影响以提高诊断策略优化的指向性，本文对其启发函数在进行了加入测试可靠度和诊断树可靠度指标的改进。改进准深度算法的实现流程如图1所示。

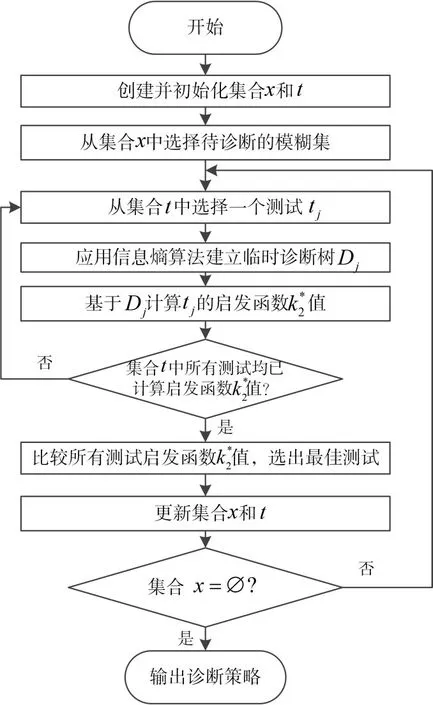
图1 改进准深度算法实现流程

具体的计算步骤如下：

1）设待测系统的初始故障状态集和初始测试集分别为x=F和t=T；

2）测试集t中每个测试tj将故障状态集x划分的子集xjp和xjf，根据式（7）计算其概率p(xjp)和p(xjf)，并采用式（11）更新各子集故障状态的概率，然后应用信息熵算法对各个子集进行诊断策略优化，并得到以tj为第一个测试的临时诊断树Dj；

3）基于Dj，应用式（12）计算tj的启发函数值：

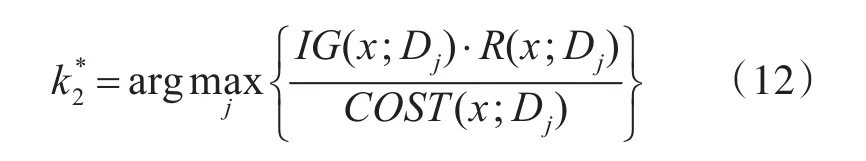
式中：IG(x;Dj)表示Dj与状态集x的交互信息，R(x;Dj)表示Dj的平均测试可靠度，COST(x;Dj)表示Dj的平均测试代价，可由式（13）～（15）计算。

式中：RDj(k)[i]表示测试序列Dj(k)中第i个被执行的测试的测试可靠度。

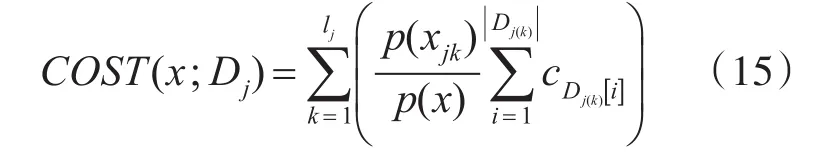
式中：RDj(k)[i]表示测试序列Dj(k)中第i个被执行的测试的测试代价。

4）选择启发函数值最大的测试并记为tk；

5）测试ts将故障状态集x划分为xsp和xsf两个子集，用式（11）更新各个子集中的故障概率；

6）将t更新为原测试集删除ts后的测试集，x更新为步骤（6）中产生的各个故障子集，重复执行步骤2）～7），直至各故障子集中不多于一个元素。

7）将依次被选择的测试ts组成诊断树Ds，输出为最优诊断策略。

4 实例验证与分析

为了验证本文方法的有效性和准确性，以文献［13］中的阿波罗检测系统为例进行实例分析。该系统共10个故障模式f1～f10，15个备选测试t1～t15，故障-测试相关性矩阵如图2所示。该矩阵是一个11×15矩阵，其中矩阵行表示故障模式（第一行为无故障状态f0），各故障模式的先验概率分别为[68,3,7,2,1,3,4,2,5,3,2]×10-2。矩阵列表示备选测试，各测试的检测概率pdj、虚警概率pfj、测试可靠度R（tj）和测试代价cj如表1所示。

图2 故障-测试相关性矩阵

应用改进准深度算法对该实例进行诊断策略优化，当采用t1为第一个测试时，它将系统故障集x分为{f0,f1,f2,f3,f4,f5,f6}和{f7,f8,f9,f10}，其概率分别为0.88和0.12。而后根据3.1节信息熵算法建立以t1为首的临时诊断树D1如图3所示。

然后基于D1，以f1为例阐述启发函数值计算过程，其测试序列为{t1,t4,t7,t11}，各参数计算过程如下：

表1 各测试点参数设置

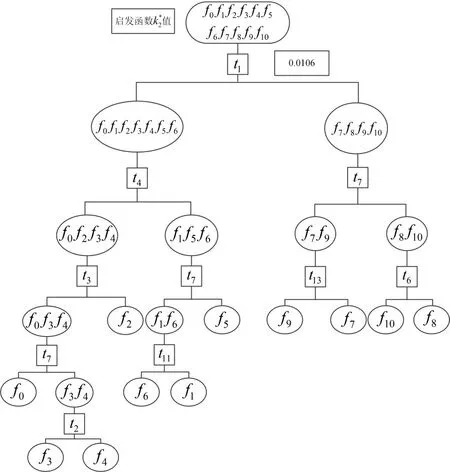
图3 以t1为首的临时诊断树

依次计算得到各个叶节点的参数，然后依据式（13）～（15）得到该临时诊断树的信息量IG(x;D1)，平均测试可靠度R(x;D1)和平均测试代价COST(x;D1)，最终根据式（12）计算得到t1的启发函数k2（t1）。具体计算过程如下：

同理，分别采用t2,t3,…,t15对系统故障状态集x构建临时诊断树，得到各个测试的启发函数分别为0.0103,0.0129,…,0.0108。选择启发函数值最大的测试点t7为第一步测试，其启发函数值k2(t7)=0.0131。

根据3.2节改进准深度算法的步骤6），将故障状态集x更新为以上计算过程中产生的各个故障子集，重复执行步骤2）～6）直至各故障子集中不多于一个元素，依次被选择的测试ts组成最优诊断测试序列。基于改进准深度算法与基于信息熵算法生成的诊断策略分别如图4、5所示。

图4 基于改进准深度算法的诊断树

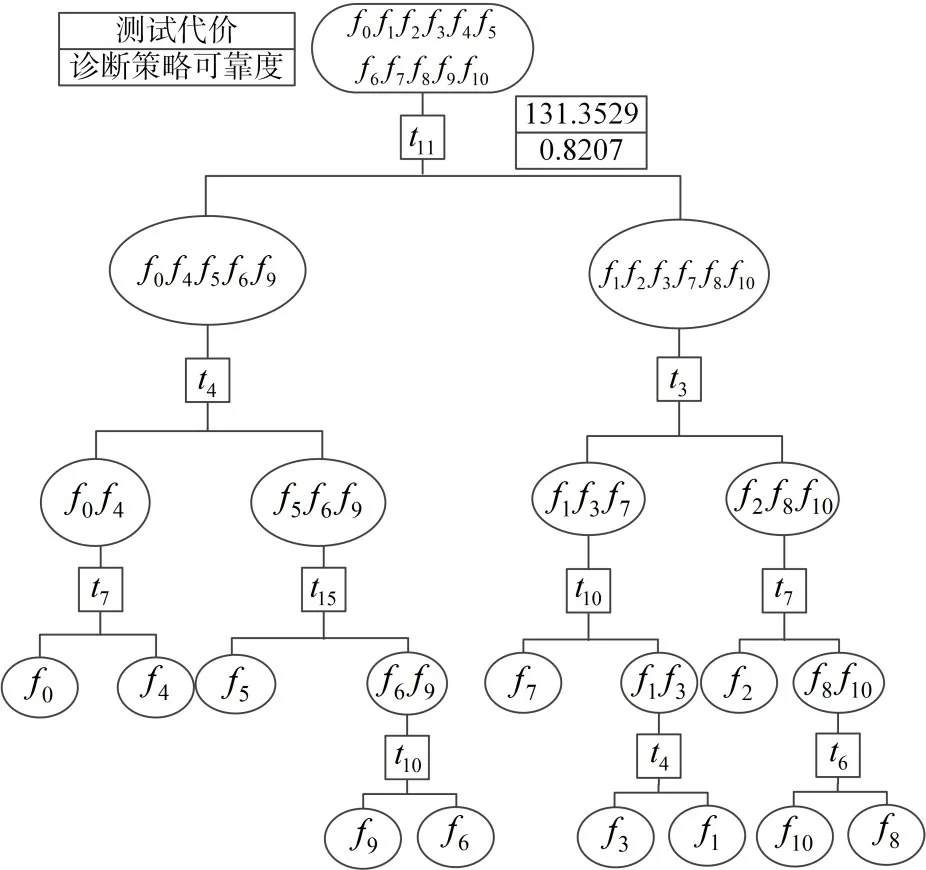
图5 基于信息熵算法的诊断树

通过对比以上两种诊断策略可知，应用改进准深度算法生成的诊断策略测试代价为117.5609，可靠度为0.8296，而单纯应用信息熵算法生成的诊断策略测试代价为131.3529，可靠度为0.8207。

通过深入分析可知，信息熵算法是基于贪婪搜索策略的，因此其在诊断策略生成过程中仅考虑了当前测试所获取的信息和测试代价，因而最优性较差，测试代价较高，测试可靠度较低。而改进准深度算法在选择当前最佳测试的过程中，不仅考虑了当前测试的信息、代价和可靠度参数，还考虑了以各个备选测试为顶点的临时诊断树的平均信息量、测试代价和测试可靠度。因此，该算法最优性要优于传统信息熵算法，并且生成的诊断策略能够以较小的测试代价检测隔离系统发生的故障，同时保证了较高的测试可靠度。

5 结语

本文针对现有诊断策略优化方法中因假设测试完全可靠而造成诊断策略优化结果不可靠，进而误诊费用增高的问题，提出了一种有指向性的选择可靠度高的测试的方法。实例分析结果显示应用本文方法时，测试代价和测试可靠性指标均有一定优势，验证了本文方法的有效性和准确性，对诊断策略设计工作具有一定的参考价值，并且相比现有的基于信息熵的诊断策略优化方法，考虑测试可靠度的诊断策略优化方法更具有实用性。