基于LS-SVM的舰艇修理能力评估研究

骆静 邹小锐

摘 要：艦艇修理能力受多种因素影响，且历史数据缺乏，为了对舰艇修理能力进行有效评估，建立了舰艇修理能力指标体系，针对小样本数据特点，使用最小二成支持向量机（LSSVM）建立修船能力评估模型，并利用粒子群算法（PSO）对影响最小二乘支持向量机（LSSVM）回归性能的参数进行优化。通过专家打分数据验证，结果表明，该方法在小样本条件下的泛化能力较好，能够科学、准确地评估舰艇修理能力，具有较高的评估效率。

关键词：舰艇修理;评估;最小二乘支持向量机;粒子群优化

Abstract： Evaluation of warship maintenance capability is limited by several factors， The historical data is lacked，In order to Evaluation of warship maintenance capability， The evaluation index system is constructed based on influence factor analysis. Focus on character of small data sets， LSSVM model is used to evaluated the warship maintenance capability， PSO is used to optimize the most important parameters which influent the LSSVM regression model. Verified by expert evaluation method， the evaluation results show， The generalization ability of model is well for small data sets， the PSO-SVM evaluation method is a scientific and accurate method for the evaluation of warship maintenance capability. The evaluation efficiency is high.

Keywords： warship maintenance; evaluation; LSSVM; PSO

1 引言

舰艇修理，是为保持和恢复舰艇的战术技术性能而采取的修理措施，它能够使舰艇在规定服役期内保持良好的技术状态和正常的在航率。修理能力评估是在开展修理工程前，对舰船修理厂的舰船修理能力的全面、准确分析和评价，以便为任务分配决策提供依据，同时也是降低舰艇修理风险，合理优化维修资源的重要保证。舰艇修理能力评估是一个多指标体系的综合评估问题，修理能力受人员、设备、技术及备品备件等多因素影响[1] [2]，且影响因子与能力评估结果之间存在非线性关系，各评价指标之间及相互独立又相互制约，如何对修船能力进行科学客观的评估是一个系统、复杂的问题。神经网络、模糊数学及层次分析法等数学方法被应用到修船能力评估中[2][3]，取得了一些成果，但上述方法都是在经验风险最小化原则下基于样本无限大的基础上进行的，而舰艇承修单位涉密程度高，修理项目繁杂，造成修理数据采集困难，样本有限，容易出现数据过拟合，泛化能力不高等问题[4]，从而限制了这些方法的应用。针对有限样本数量的情况，Vapnik等人对机器学习进行了系统的研究，而支持向量机（Support Vector Machine，SVM）是在小样本情况下机器学习规律下构造的机器学习方法，它以统计学习理论为基础，结构风险最小化为准则，对修船能力评估这类有限训练样本的问题，表现出数据预测精度高、不受数据维数限制等优点。当训练样本过大时，支持向量机因约束条件过多导致训练时间长，无法满足工程需要，最小二乘支持向量机（LSSVM）采用二次规划方法将支持向量机中的不等式约束改为等式约束，以误差平方和损失函数作为训练集的经验损失，把二次规划问题转化为求解线性方程组问题，加快了问题求解的速度，提高了算法的收敛精度。该方法已广泛应用于数据预测及评价领域，取得较好的效果[4]- [9]。本文在分析分析舰艇修理影响因子的基础上建立了修船能力评估指标体系，使用最小二成支持向量机（LSSVM）建立修船能力评估模型，利用粒子群算法（PSO）对影响最小二乘支持向量机（LSSVM）回归性能的参数进行优化，并对模型的评估有效性和准确性进行了检验。

2 修船能力评估指标体系构建

2.1 评价指标建立的原则

在科学开展修船能力评估前，需要对修船能力影响因素进行分析，建立一套客观合理的评估指标体系，也是建立修船能力评估模型的前提。考虑舰艇修理实际，评估指标体系构建需遵循以下原则：

客观性原则：评估指标立足修船工程实际，能够直接或间接体现出修船能力，指标尽量降低评价系统人为主观因素影响。

易量化原则：指标能够通过工厂实力及历史数据获得，并通过相应数学模型进行量化，作为评估模型数值输入。

多维性原则：修船能力评估指标应覆盖修理全过程，充分考虑修理周期、修理质量和修理费效等多个因素。

连续性原则：修船能力评估不是孤立的，它是修理企业前提修理能力的延续，评估结果也为后续任务承接提供理论依据。

战斗力标准原则：除以上通用原则外，针对作战舰艇特点，还需要考虑舰艇战技指标恢复程度，该项指标与特装修理人员数量及技术水平、修理任务均有关系。

2.2 评价指标的建立

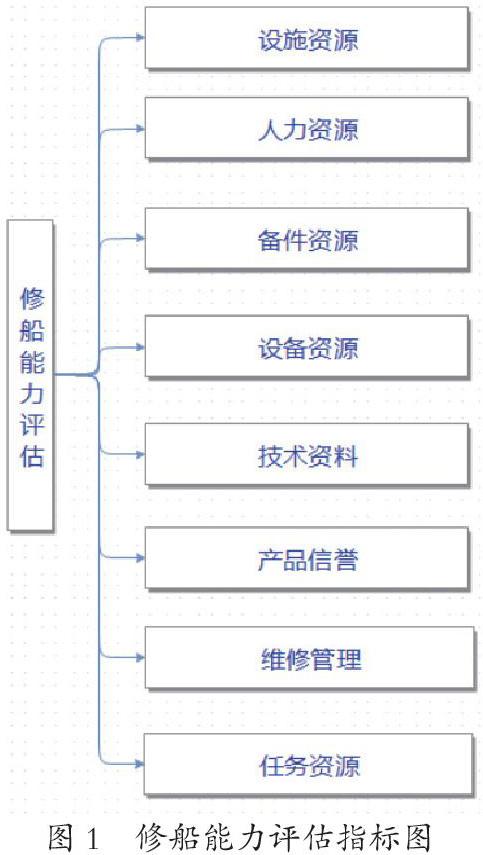
在严格遵循以上原则的基础上，本文从修理资源、修理效果、修理管理及修理任务四个主要影响方面来确定评估指标。其中修理资源通过设施资源、人力资源、备件资源、设备资源及技术资料5个具体指标来确定;修理效果通过产品信誉来表示，该指标主要为修理企业所修理前期所承担舰船修理效果的综合评价;修理管理为多级指标，分企业管理、部门调度、班组分工等多个层级;修理任务通过任务资源这个指标来体现，任务资源可推进修理企业人力资源和基础设施投入，进而提升企业舰艇修理能力水平，该指标充分体现了连续性原则。修船能力评估指标如图1所示。

3基于最小二乘支持向量机的修船能力评估建模

3.1 基于最小二乘支持向量机的修船能力评估模型

最小二乘支持向量机利用最小二乘线性系统误差平方和损失函数作为训练数据集的经验损失，将不等式约束规划转换成等式约束，将二次规划问题转化为线性方程组的求解，提高了模型的解算速度[11]。舰艇修理历史数据xi作为输入数据，，yi为与相对应评估指标的评估结果，，将评估样本过非线性映射函数映射到高维特征空间中，这样把评估模型中非线性不可分问题转化为高维空间的线性可分问题：

式3-1中，ω表示特征的权值向量，b表示特征的偏置量。结合最小化结构风险的原则可以将式3-1优化目标为：

式3-2中，γ作为误差的可调参数，ξi作为误差变量。对式3-2进行约束优化转换为无约束对偶空间的问题需要通过引入Lagrange乘子来解决，定义Lagrange函数为：

式3-3中，αi为Lagrange乘子。根据Karush-Kuhn-Tucker（KKT）互补条件的约束条件存在如3-4关系：

对3-4进行化简，消除ω和ξi能够得出式3-5矩阵列

针对舰艇修理能力评估问题，根据Mercer条件，将式3-5转换为线性预测。

径向基核函数是一种局部性强的核函数，可以将一个样本映射到更高维的空间内，对大小样本都有较好的性能，本文选取作LS-SVM的核函数，估计回归函数为式3-7：

3-7式中，σ为核参数，代表均方差的高斯函數。

3.2基于粒子群算法的LSSVM模型参数选取

在最小二乘支持向量机的回归模型中，惩罚参数C和核参数σ是影响最小二乘支持向量机学习精度和泛化能力的两个参数。模型参数的选择问题实质上是一个优化问题，目前参数选择方法有：经验选择法、实验试凑法、网格搜索法。经验选择法、实验试凑法过多依赖于经验值，主观性太强;网格搜索法计算量较大，且以上方法并不能保证找到全局最优解。本文使用粒子群算法对这两个参数进行优化。

粒子群算法是一种基群体叠代的启发式优化方法。它与遗传算法有相似的地方，它们都是一种基于的过程， 基于粒子群优化最小二乘支持向量机参数算法实现如下：

1）选取训练样本数据并进行数据预处理，初始化最小二乘支撑向量机（LSSVM）和粒子群算法（PSO）参数;

2）根据经验和试算确定（C，σ）的大致范围，初始化所有粒子，设置粒子的初始位置和速度，每个粒子的初始位置设为pbest，pbest中的最好值即为gbest;

3）计算每个粒子的适应值;

4）对每个粒子，将其适应值与其经历过的最好位置pbest的适应值进行比较，如果优于pbest，则将其作为当前的最好位置pbest，同时将其适应值与种群所经历过的最好位置gbest的适应值进行比较，如果优于gbest，则将其作为种群最优位置;

5）检验是否符合结束条件。如果迭代次数已达到最大迭代次数或用已搜索到的最优位置计算出的适应值已满足给定适应值的要求时，则停止迭代，否则转步骤3;

6）用得到的优化初值作为LSSVM的惩罚因子和核参数，训练样本得到LSSVM模型 [5]。

3）利用优化后的参数对最小二乘支持向量机的回归模型进行重新训练;

4）根据修船指标体系中设施资源、人力资源等9个评估指标历史数据，使用训练好的回归模型对修船能力进行评估。

3.3 修船能力评估数据的选择

选取设施资源、人力资源、备件资源、设备资源及技术资料等9个指标来对修船能力进行评估，指标样本数据来源于历史数据，对于不易定量的指标采用专家打分法进行量化。以修船能力评估等级作为模型训练输出数据。

3.4 数据的归一化整理

为减小数据大幅波动对预测效果的影响，提高评估模型的收敛速度，需对样本数据进行归一化处理。归一化公式为：

式中：yi是训练样本中某一变量数据xi归一化后数据，xmin为样本中改组变量数据的最小值，xmax为样本中该组变量数据的最大值。

4 仿真验证

4.1 样本数据采集

本文采集某舰艇修理企业140个舰船修理数据作为评估样本，取前112个样本作为PSO-LSSVM的训练样本（部分训练样本见表1），后28个样本作为测试样本（部分训练样本见表2）。根据指标评估体系，选取影响修船能力9个主要因素的数据作为模型的输入向量，模型的输出为4个等级，分别为4（优）、3（良）、2（中）、1（差）。

4.2 模型参数设置及仿真结果分析

Matlab编写了PSO-SVM程序，通过试算确定PSO的参数如下：粒子个数为30，粒子维数为2，循环次数为300，学习因子c1=1.5，c2=1.7，参数c的搜索范围为（0.1，100），参数g的搜索范围为（0.01，1000）。经过PSO优化，得到LSSVM的最优参数对c=8.7246，g=0.04，其优化结果图见图2。

利用最优参数对c=8.7246，g=0.04来建立LSSVM模型，为了检验模型的有效性，使用训练好的模型对表2中28组测试样本进行评估，与专家打分方法的评估结果进行对比，其评估结果如图3所示，所对应的评估数据如表2所示。

从图2和表2中可以看出PSO-LSSVM方法的评估效果都较好，总共有28组测试样本，使用PSO-LSSVM方法进行评估，经数据处理，所有28组与专家打分法的评估结果相吻合，评估准确率较高。

5 结论

针对修船评估数据小样本特点，使用最小二成支持向量机（LSSVM）建立修船能力评估模型能较好的描述修船能力与其影响因素之间的非线性关系，并利用粒子群算法（PSO）解决了对影响最小二乘支持向量机（LSSVM）回归性能参数选择问题。通过仿真实验验证，该模型能够有效地对修船能力进行评估，准确度较高，为修船能力评估提供了新的手段。

参考文献：

[1]张荧锋，陈砚桥.中继级修理能力评估指标体系研究[J]. 中 国 修 船. 2006.19（8）

[2]田 华，朱建冲.基于 BP 神经网络的海军中继级修理能力评估[J]. 控 制 管 理，2007.1

[3]黄栋，张怀强. 基于模糊层次分析法的舰船装备承修单位承修能力评估[J]. 中国修船，2008.8

[4]阮永芬，高春钦.基于粒子群优化小波支持向量机的岩土力学参数反演[J].岩土力学，2019.9

[5]胡新江，徐浩军.加权 LS-SVM的航空装备维修保障能力评估模型[J].火力与指挥控制，2012.12

[6]韩创益，王恩德. 基于贝叶斯推理的 LSSVM 矿产资源定量预测[J].东北大学学报，2017.11

[7]黄玉清， 魏军.基于SVM的舰船装备维修外购外协件质量监控研究[J].舰船科学技术，2010.7

[8]朱家元， 郭基联. 多元分类LS-SVM设计与装备保障性评估 [J].装备指挥技术学院学 报，2003.6

[9]肖斌卿，柏巍.基于LS-SVM的小微企业信用评估研究[J].审计与经济研究，2016.6

[10]黄丽君，郭文忠.基于粒子群优化的BP神经网络预测方法及其应用研究[J].漳州师范学院学报（自然科学版），2008.1

[11]叶永伟，陆俊杰.基于LS-SVM的机械式温度仪表误差预测研究[J].仪器仪表学报，2016.1

作者简介：

骆静（1984—），女，湖北武汉人，现为中船黄埔文冲船舶有限公司修船事业部技术部工程师。

邹小瑞（1976—），男，重庆人，现为中船黄埔文冲船舶有限公司修船事业部技术部研究员。

（中船黄埔文冲船舶有限公司 修船事业部技术部，广东 广州 510000）