±800 k V输电线路带电作业电位转移电流计算模型优化

李金亮，杨淼，隆晨海，任卉嵩，雷冬云，曾益

(1.国网湖南省电力有限公司电力科学研究院，湖南长沙，410007；2.国网湖南省电力有限公司检修公司，湖南长沙，410004；3.国网湖南省电力有限公司长沙供电公司，湖南长沙，410015；4.国网湖南省电力有限公司邵阳供电公司，湖南邵阳，422000)

0 引言

随着经济快速发展,建设特高压输电线路成为我国能源和经济社会协调发展的必然要求。因特高压直流输电线路输送容量大、运行可靠性要求高,特高压直流输电线路带电作业已成为确保特高压直流电网长周期安全稳定运行的重要技术手段。为确保特高压直流输电线路带电作业人员安全,需对电位转移电流进行仿真计算,以便为等电位作业人员安全防护措施提供依据[1-5]。

以±800 kV直流输电线路带电作业转移电流的计算为例,等电位作业人员采用吊篮法进入等电位。传统的计算电位转移电流的模型为电容模型,主要包含三个导体之间的电容,等电位作业人员及吊篮作为一个导体,进行电位转移的极线作为一个导体,另外一根极线、杆塔、地线和大地作为一个导体。虽然另外一根极线距离等电位作业人员较远,但由于特高压输电线路电压等级高,其对电位转移电流的影响也不容忽视。本文将传统计算转移电流的电容模型进行改进,考虑另外一根极线的影响,改进后的电容模型则主要包含四个导体之间的电容。通过有限元法对上述两种模型情况下的电容进行仿真计算,基于计算出的电容参数,仿真计算出上述两种模型在不同转移距离下的转移电流,并进行对比。改进后的电容模型从物理意义上更加准确,其研究结果可为输电线路带电作业转移电流的计算提供参考。

1 转移电流计算模型

电位转移是指作业人员通过导电手套或其他专用工具 (如电位转移棒)从中间电位转移到等电位的过程,是带电作业进出等电位过程中最重要的环节。由于特高压输电线路电压等级高,在电位转移的瞬间,会有较大的脉冲电流,在此过程中防护措施不当极有可能出现安全事故,因此电位转移过程中的脉冲电流是带电作业安全防护需要考虑的[6-10]。

1.1 传统的电容模型

采用吊篮法在进入±800 kV直流输电线路等电位的过程中,可采用如图1所示的传统电容模型对作业人员进入等电位过程中的电容暂态放电电流进行计算,其中,R为接触电阻；U为导线工作电压；L为转移棒和屏蔽服的电感；C12为人体与导线之间的电容；C11为人体对地电容。此时,在计算电容参数时,将人体及吊篮定义为导体1,将进行电位转移的极线定义为导体2,将铁塔、地线、大地及另外一根极线定义为导体3。在传统电容模型中,将另外一根极线与大地定义为一个导体,由于另外一根极线电压等级较高,因此采用传统电容模型可能会影响转移电流的计算精度。

图1 传统的电位转移电流计算模型

1.2 改进后的电容模型

为提高采用电容模型计算转移电流的精度,需考虑另外一根极线对电位转移电流的影响,并由此建立的电容模型如图2所示。其中,R为接触电阻；U1为等电位作业人员进行电位转移的导线工作电压；U2为另外一根导线的工作电压；L为转移棒和屏蔽服的电感；C12为人体与所需进行电位转移的导线之间的电容；C13为人体与另外一根导线之间的电容；C11为人体对地电容。此时,在计算电容参数时,将人体及吊篮定义为导体1,将进行电位转移的极线定义为导体2,将另外一根极线定义为导体3,将铁塔、地线及大地定义为导体4。

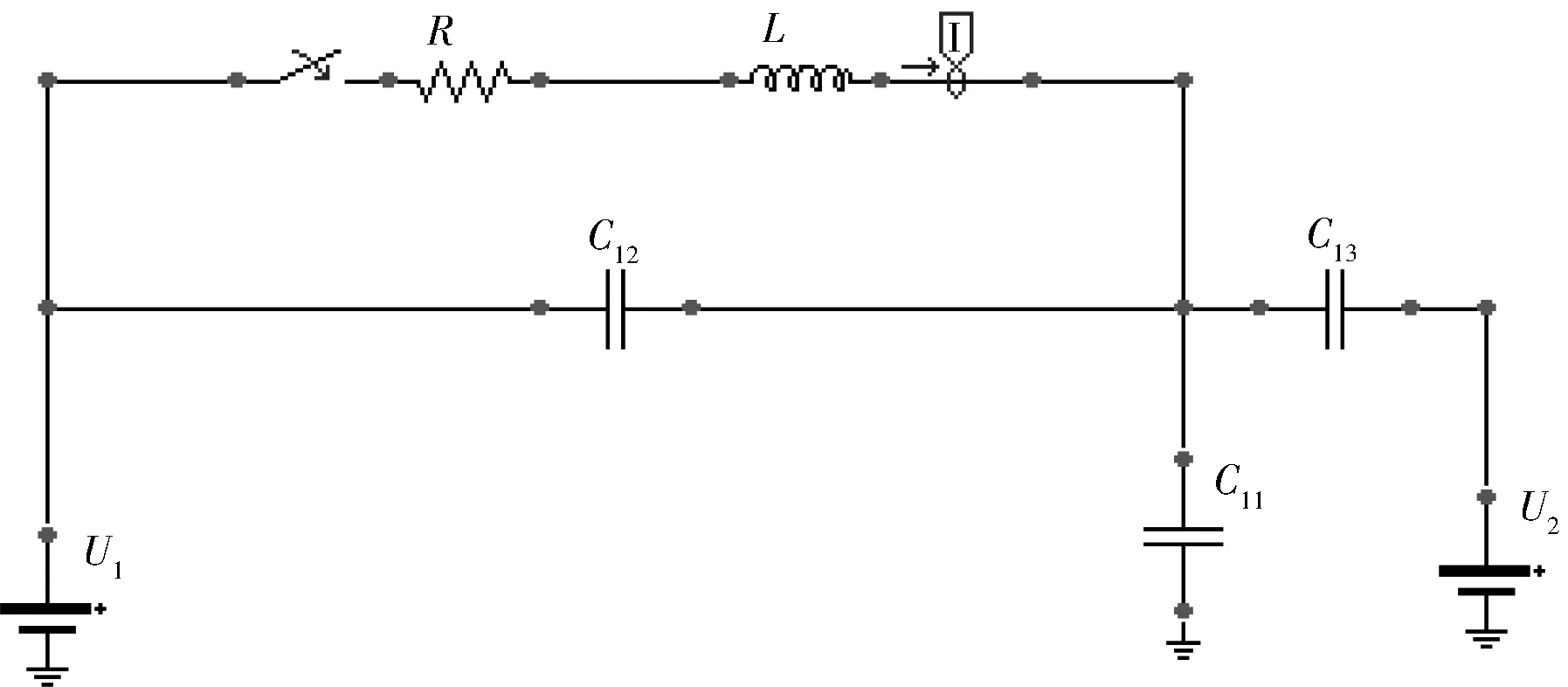
图2 改进后的电位转移电流计算模型

2 电容参数计算

以改进后的电容模型为例,多导体静电系统所储存的总静电能量计算如下:

其中,Cij(i≠j,i,j＝1,2,3) 为导体i与导体j之间的电容；Cii(i＝1,2,3)为导体i的对地电容；E为电场强度矢量；D为电通密度；ui为第i个导体对地电压；qi为第i个导体所带电荷。

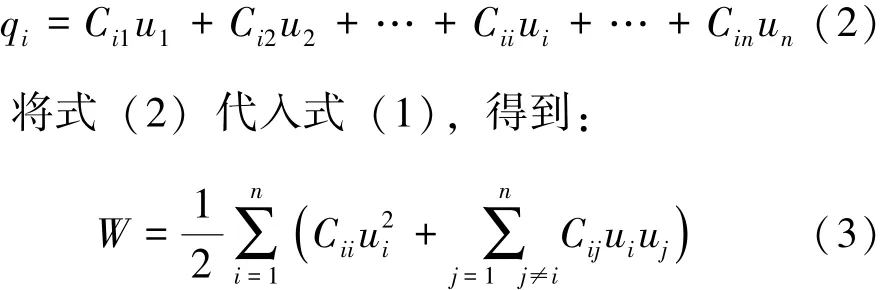
具体的部分电容求解过程如下:

1)主对角线元素Cii:给第i个导体施加单位电压,其余n-1个导体设零电位,利用有限元法求解三维静电场,再由式 (1)得到空间中的能量Wii,根据式 (3)可解得Cii(i＝1,2,3)。

2)非对角线元素Cij:给第i,j导体施加单位电压,其余n-2个导体设零电位,利用有限元法求解三维静电场,再由式 (1)得到空间中的能量Wij,由于Cii已知,再根据式 (3)可解得Cij(i≠j,i＝1,2, …,n-1,j＝i+1…n)。

采用吊篮法进行电位转移的现场作业情况如图3所示,根据±800 kV输电线路带电作业现场布置情况建立有限元计算模型[11-13],计算出的电位分布如图4所示,且云图结果与实际相符。

图3 吊篮法进入电场

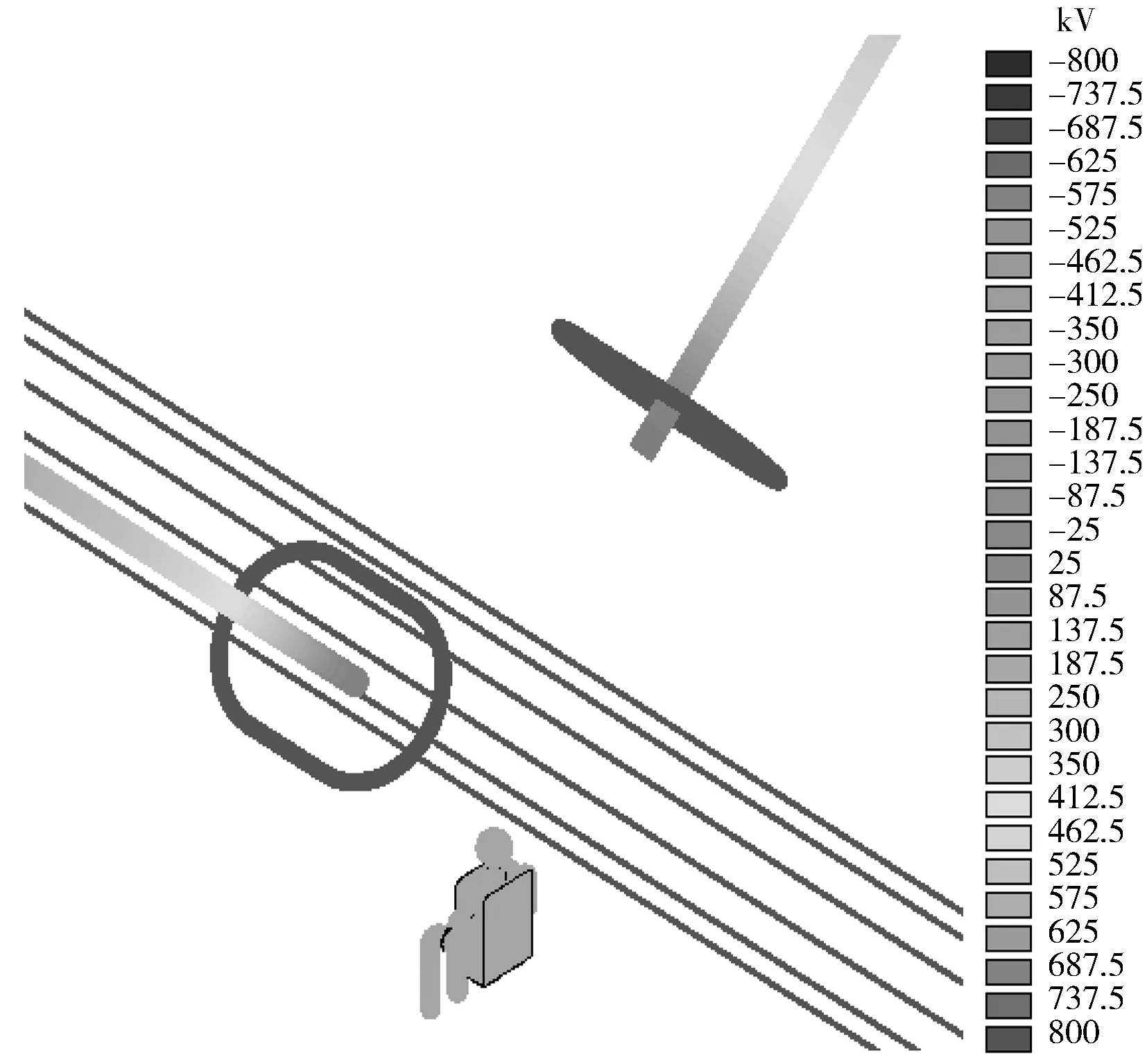
图4 吊篮法进入电场电位分布

根据上述公式,采用有限元法可计算出电容参数。当转移距离为0.3 m时,由此计算出的电容参数见表1。

表1 电容计算结果 pF

从表1的计算结果可以看出,由于人体与需进行电位转移的极线距离较近,与另外一根极线距离较远,因此C13较C12小很多,但由于另外一根极线的工作电压较高,其对转移电流的影响不容忽视。

3 转移电流仿真计算

3.1 传统模型和改进模型的转移电流计算结果对比

两种模型中,接触电阻为R取300Ω,电感为L取0.01 mH。采用电磁暂态仿真软件,基于图1和图2所示的两种电容模型,对电位转移瞬间的转移电流进行了计算,当转移距离为0.5 m时,以传统电容模型为例,计算出的转移电流波形如图5所示。

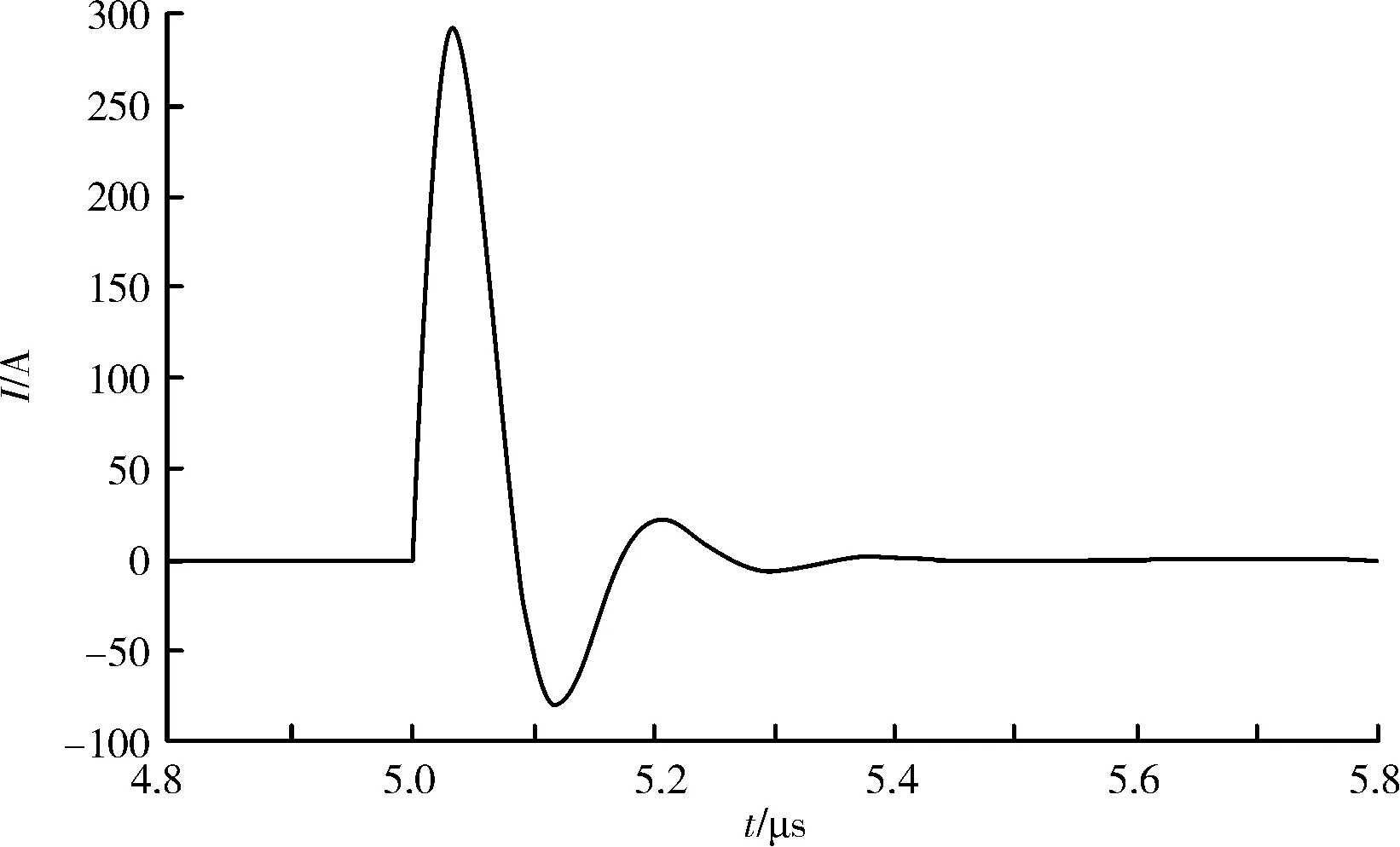
图5 电位转移电流波形

采用传统的电容模型计算转移电流,转移距离为0.5 m时,可计算出等电位过程中电容暂态放电电流的峰值为292 A。采用改进的电容模型计算转移电流,转移距离为0.5 m时,可计算出等电位过程中电容暂态放电电流的峰值为303 A。改进后的电容模型计算出的转移电流比改进前的模型计算出的转移电流大11 A。因此,为提高计算的精度,应考虑采用改进后的电容模型计算转移电流。

为校验现有防护措施是否得当,采用改进的电容模型对电位转移能量进行计算,发现当转移距离为0.5 m时,等电位作业人员与导线的电位差为222.4 kV,转移能量为1.0 J；当转移距离为0.7 m时,等电位作业人员与导线的电位差为247.1 kV,转移能量达到1.16 J。相关文献的研究结果表明,采用导电手套对电位转移过程的放电特性进行模拟,当放电系统能量约为1.37 J时,放电电弧的根部直接作用在导电手套上,将手套烧蚀[14]。所以在实际作业中采用电位转移棒进行电位转移以确保作业人员安全,采用改进的电容模型进行转移能量的计算,计算结果不影响现有防护参数的选择。

3.2 不同转移距离下的转移电流计算

为分析两种电容模型计算出的转移电流变化规律,仿真分析两种模型情况下不同电位转移距离(0.3 m、0.4 m、0.5 m、0.6 m、0.7 m)下的转移电流波形,并计算出最大值,其随转移距离变化规律的曲线如图6所示。

图6 不同转移距离下转移电流峰值

由图6可看出,采用改进的电容模型计算出的转移电流较传统的电容模型计算出的转移电流大,且两种模型计算出的转移电流峰值随转移距离的变化规律一致,即随着转移距离的增大,转移电流增大。这是由于在进入等电位过程中,人与导线之间的电位差逐渐降低,人体与进行电位转移的导线距离越远,人体与需进行电位转移的导线之间的电容储存的能量越大,因此转移电流也就越大[15]。

4 结语

本文对计算转移电流的传统的电容模型进行了改进,并依据±800 kV直流输电线路带电作业现场实际情况,建立仿真模型,分别对电容参数和转移电流波形进行仿真计算,可得到如下结论:

1)采用改进的电容模型计算出的转移电流较传统的电容模型计算出的转移电流大,为提高计算精度,尤其对于电压等级更高的输电线路,转移电流的仿真计算应考虑采用改进的电容模型。从转移能量的计算结果来看,采用改进后的电容模型进行分析不影响现有防护参数的选择。

2)两种电容模型计算出的转移电流峰值随转移距离的变化规律一致,即随着转移距离的增大,转移电流增大。