基于EMD算法的双外腔激光自混合微振动测量

高丙坤,刘径舟,张子超

(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.廊坊市中燃宏胜能源科技有限公司,河北 廊坊 065000)

1 引 言

激光自混合干涉(SMI)现象是指激光器发出的激光照射到外部振动目标上,经反射或散射后一部分携带了目标振动信息的激光反馈回激光腔并与腔内激光进行混合,使得激光器输出光功率发生变化,从而形成激光自混合干涉。因反馈光会改变激光参数而导致测量误差,因此早期的研究者们将从外部物体表面反馈回激光器谐振腔的光视为干扰因素,致力于减轻反馈光对激光器的输出特性产生的不利影响。随着研究的逐渐深入,研究人员发现反馈回的激光携带有外部振动物体的运动状态信息,于是开始不断探索激光自混合信号的特性及其应用。

从20世纪80年代开始,激光自混合干涉技术逐渐应用于测量领域。随着激光器种类的不断丰富[1]以及激光器技术的完善,如今激光自混合干涉技术已经逐渐趋于成熟。之前的研究工作主要围绕着半导体激光二极管的自混合干涉展开。由于半导体激光器易于产生自混合现象,并因其具有精度高、易准直、成本低等特点,在很多领域都有应用,例如,对目标物体的振动进行测量[2-4],距离测量[5]以及速度测量等[6-9]。在齿轮箱故障诊断[10-11]以及管道泄漏检测[12]等工业领域也有着广泛的应用前景。近年来,研究人员在测量装置上进行了部分改进[13-15]。已经开始利用全光纤自混合干涉仪进行自混合干涉的研究。光纤具有优越的可靠性,抗电磁干扰能力和长距离传输能力[16]。目前对自混合信号的研究已拓展到双外腔结构[17],并构造了含有两路反馈外腔结构的自混合干涉模型,证实了两路反馈外腔结构的自混合干涉信号为幅度周期性变化的类正弦波或类锯齿波[18]。两路外腔反馈的激光自混合干涉,即采用一个激光二极管,外腔由一路拓展到两路。在激光器数量不变的情况下能够采集到含有两路振动信息的激光自混合干涉信号,拓展了测量通道。但由于两路外腔自混合信号在频域上混叠,频谱分析方法难于彻底分离两路信号,使得已有的单路自混合干涉信号的微位移测量方法无法直接应用于两路信号振动信息的提取。宦海等人利用希尔伯特变换方法实现了两路合成信号的重构,但是其中的小波基及阈值函数不容易选择[19]。

为了实现两路微位移的同时测量,本文新提出了一种方法,用经验模态分解(EMD)算法对不同频率的两路激光自混合信号进行分离,对比于希尔伯特变换方法,具有算法简洁的优势。以原始信号和各基本模式分量(IMF)的互相关系数作为判断依据,选择出高频一路所需的IMF分量。对分离得到的两路自混合信号分别进行傅里叶变换,根据各自的频谱进行分析,从而提取出两路信号所携带的各路外部运动物体的振动信息。

2 两路自混合原理

两路自混合信号的外腔结构如图1所示,激光器发出的光束通过分光镜分成两束,一束折射到目标物体1上,一束透射到目标物体2上。经目标运动物体反射回分光镜处,最终返回激光器内腔,形成了两路自混合干涉。

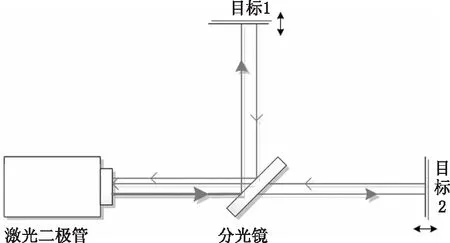
图1 两路自混合外腔结构光路图

已有文献[20]的研究表明,双外腔自混合信号为两个单路自混合信号的叠加。叠加能够保留两路信号各自的波动趋势,这是以下用EMD方法进行两路自混合信号分离的基础。

3 理论分析

EMD方法的本质可以理解为对信号进行平稳化处理,然后逐级分解出信号中含有的不同尺度的波动或者趋势,分解出的各个分量称作固有模态函数IMF。IMF分量通常在某一时刻只存在一种固定的频率成分[21]。

固有模态函数一般需要满足下面的条件。在IMF中不能出现大于零的极小值以及小于零的极大值。理想的信号应当局部均值为零。按定义,每次分解运算得到的IMF分量振荡的模式不可复杂,应为单一模式,且为存在有意义的瞬时频率的单分量信号。EMD分解过程如下[22]:

确定两路自混合信号S的所有局部极值点,构造上下包络线,即将所有局部极大值点用三次样条线连接起来形成上包络线,将所有局部极小值点用三次样条线连接起来形成下包络线。对上下包络线取的平均,记为M1。若原始信号减去M1为IMF分量,记:

IMF1=I1=S-M1

(1)

若I1不为IMF 分量,则对I1继续取包络求得平均值M11

I11=I1-M11

(2)

I1n=I1(n-1)-M1n

(3)

若I11为IMF分量,IMF1=I11；若不为,则上式重复n次直到I1n满足固有模态函数条件。此时得到第一个高频分量

IMF1=I1k

(4)

使原始两路自混合信号去掉第一个高频分量得到的信号命名为L1。重复上面步骤。

L1=S-IMF1

(5)

Ln=Ln-1-IMFn

(6)

当Ln单调递增或递减时分解结束。

(7)

若忽略噪声影响,则等式右侧的两部分分别为分离出的高频与低频信号。

对分离出的信号进行傅里叶变换与频谱分析,由公式(8)可求得两路目标的振幅。其中nd为主频阶次。

(8)

4 仿真数据处理

仿真数据为微弱反馈水平(C≪1)的信号。如图2所示,频率分别为10 Hz与频率为300 Hz的SMI信号,以及由这两路SMI构成双外腔激光混合信号的仿真图。由图可以看出,双外腔自混合干涉信号近似于两路自混合干涉信号的叠加。

图2 双外腔SMI仿真信号

对两路自混合信号进行EMD分解,得到由高频到低频的13个IMF分量。对IMF分量做互相关运算,其中相关系数越高相关程度越大。由表1中可看出IMF1分量即为高频一路的SMI信号。根据双外腔自混合信号的线性叠加性,低频一路的SMI信号为其余12个IMF分量叠加。其分离出的两路SMI信号如图3所示。

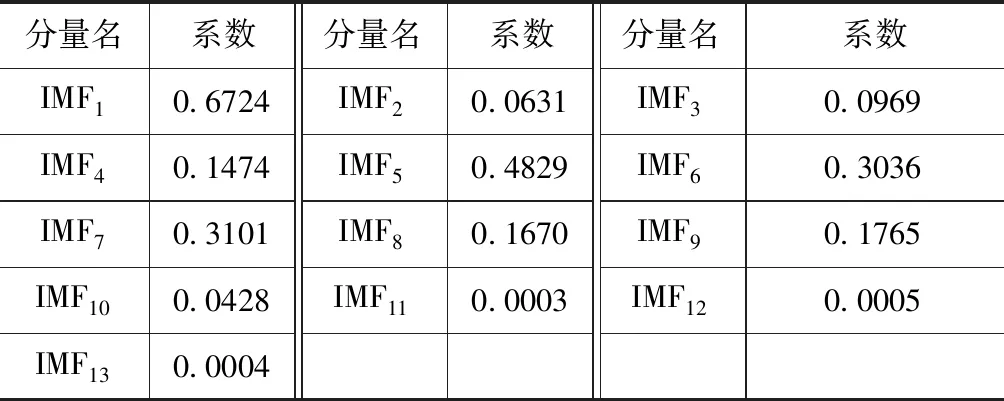
表1 各个IMF分量与原始两路信号的互相关系数

在EMD相关计算中,由于分离出的IMF分量均应具有局部对称性,所以需要用极大值和极小值定义的包络的局部均值来替换实际的均值。这可以避免由于信号的非平稳性所产生的影响,但是也会由于信号的非线性变形而引入一些假频。这就是图3(c)和3(d)中存在毛刺的原因。

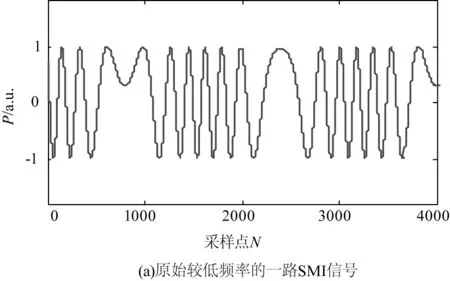
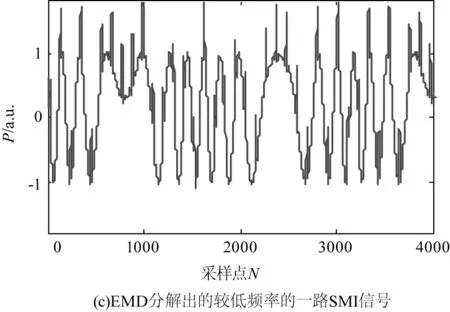
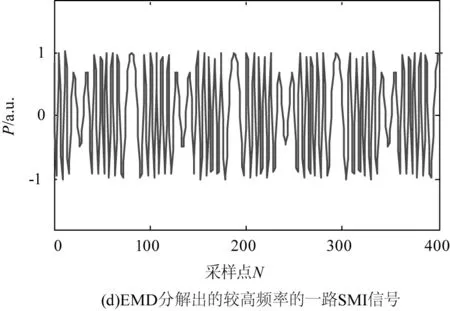
图3 单路原始自混合信号与双外腔分离后自混合信号仿真对比图

对原始信号与分离出的信号进行互相关,可得到原始高频信号与分离出的高频信号的相关系数为0.9565,原始低频信号与分离出的低频信号的相关系数为0.9523,信号得以分离。

对EMD分解后的信号进行FFT变换,频谱图如图4以及图5所示。

图4 EMD分解出的较低频率的一路SMI信号频谱

一般地,基波频率就是载波频率,为频谱图中第一个尖峰处。从图4可提取出基波频率fb为10 Hz,主频fd1为170 Hz,计算得到主频阶次nd值为17。

2.用户管理功能。以设备、功能和输出额度为标准来轻松管理单个使用者和使用群组的使用权限。从设置到输出作业，将认证程序简洁化和自动化。所有设备的绝对安全和授权使用。

图5 EMD分解出的较高频率的一路SMI信号频谱

从图5可提取出基波频率fb为300 Hz,主频fd1为5100 Hz,计算得到主频阶次nd值为17。根据公式(8)可以计算出重构振幅值为0.99 μm,其中λ0为650 nm。

双外腔激光自混合的两个目标的振动频率改变时,使用EMD分解算法的测量误差结果如表2所示,两路目标的微振幅的重构误差均小于1 %。

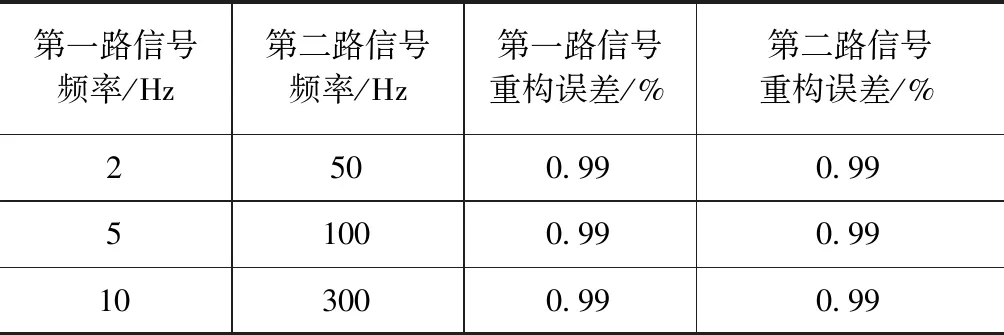
表2 利用EMD算法对不同频率的仿真信号振动重构的误差测量结果

5 实验数据处理

实验装置为简单的光纤传输自混合干涉测量系统。其配置包括光纤耦合激光器(THORLABS,S3FC1550),配有热电冷却器,可将其温度保持在恒定值,以稳定输出波长。耦合器(THORLABS,10202A-50-FC),定焦准直器(F220FC-1550)两个固定了反射镜的压电传感器(PZT)(P753.1 CD,Physik Instrumente,Karlsruhe,德国)和(P752.1 CD,Physik Instrumente,Karlsruhe,德国),光电二极管(THORLABS.PDA10CS-EC),以及 数据采集卡[National Instrument(NI),USB-4431]。其中PZT是由正弦电压信号驱动的。

图6为实验装置图,PZT表面贴有反光镜,由电脑控制振动。

图6 两路光纤传输自混合干涉测量系统装置图

PC端采集到的信号进行简单的滤波处理得到的信号如图7所示。

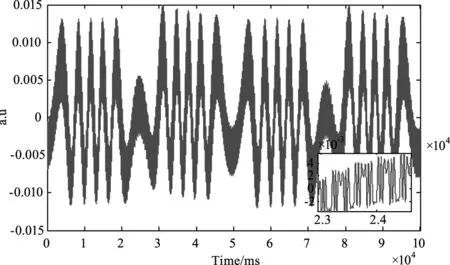
图7 去噪后的两路自混合实验信号

EMD分解去噪后的两路自混合实验信号得到7个IMF分量。对分离出的IMF分量与原始两路自混合信号进行互相关运算得到相关系数并绘出折线图。由图8可看出第四个分量与原始信号最为接近,第一个分量其次。以此为分界,较高频率一路信号为前三个IMF分量加和,较低频率一路信号为后四个分量叠加。图9为分离后的两路实验信号图。

图8 IMF分量与原始实验信号的互相关系数

图9 分离后的两路实验信号图

图10 EMD分解出的较高频率的一路SMI信号频谱

从图10可提取出基波频率fb为60.42 Hz,主频fd1为423.7 Hz,计算得到主频阶次nd值为7。根据公式(8)可以计算出重构振幅值为1.066 μm,其中λ0为650 nm。由于设置的实际振动为1 μm,求得误差为6.6 %。

图11 EMD分解出的较低频率的一路SMI信号频谱

从图11可提取出基波频率fb为0.4612 Hz,主频fd1为6.457 Hz,计算得到主频阶次nd值为14。根据公式(8)可以计算出重构振幅值为求得:1.975 μm,其中λ0为1550 nm,由于设置的实际振动为2 μm,求得误差为1.25 %。

6 结 论

在微弱反馈水平条件下,基于两路自混合信号的线性叠加性,提出了一种双外腔自混合信号的分离方法,实现了两路微振动的同时测量。用EMD算法分离两路自混合信号,采用互相关算法,以原始的两路自混合信号与各IMF分量的互相关系数作为判断依据,以得到相关系数最高的IMF分量为分界,前半部分IMF分量的叠加为高频一路所需的信号。低频一路信号由原始信号减去高频一路信号得到,也可由后半部分IMF分量的叠加求得。对分离出的两路信号进行傅里叶变换,利用主频阶次判定法重构目标物体振幅。仿真及实验结果表明,基于EMD的分离方法能够有效分离两路自混合信号。