风速和风偏角对斜拉索风雨激振的影响

关 健，李自林

(1.天津城建大学 土木工程学院，天津市西青区津静路26号 300384；2.河北水利电力学院 土木工程学院，河北省沧州市重庆路1号 061001)

近年来我国斜拉桥工程发展迅猛，随着桥梁跨度不断增加，斜拉索的刚度和阻尼越来越小,因此斜拉索极易发生振动的问题也日益突出，其中风雨激振振幅最大，危害最为严重。所谓风雨激振是指在一定天气条件下，斜拉索受到风雨的共同作用，之后发生的低频率、大幅度的振动现象。自从1984年，Hikami等[1]首次观测到该现象以来，世界多地区都出现了类似报道。随后很多学者，如Yamaguchi[2]、Seidel和Dinkler[3]、Xu和Wang[4]、顾明[5]、李永乐[6]等纷纷提出多种理论对风雨激振产生机理以及相关参数进行研究。研究结果表明，上水线的形成和振荡对风雨激振的产生和发展有重要影响。由于实际水线在斜拉索表面的形态多样，变化快，尺度小，难以准确测量，单纯依靠现场观测和风洞试验的方法不足以全方位掌握其变化规律。随着计算机技术的快速发展，计算流体力学(CFD)数值模拟技术逐渐成为研究复杂风雨激振问题的有力工具之一。李寿英和顾明等[7-8]通过流体计算软件CFX5.5建立了斜拉索的数值模型。敬海泉等[9]根据边界层状态提出一个新的数值模型来描述拉索表面的风场，系统分析了多个因素对风雨激振特性的影响。陈文礼等[10-11]应用自编译程序，提出气泡破裂的理论并对风雨激振现象进行模拟。Lemaitre等[12]首次基于滑移理论，初步建立了二维水平静止斜拉索表面的水膜运动方程，并初步模拟了水线的形成。由于该理论能准确反映斜拉索表面水膜变化形态，多名学者[13-18]在此基础上先后考虑了重力、表面张力、斜拉索倾斜角度、斜拉索振动、随时间变化的气动力等因素的影响，现已逐步发展为研究风雨激振问题的重要方法。

文中应用基于滑移理论的斜拉索风雨激振理论模型，考虑斜拉索振动与斜拉索表面水膜形态变化两者之间的关系，并应用COMSOL与MATLAB相结合的方法计算随时间变化的气动力系数，大幅提高了计算效率。通过42组数值模型，研究了不同风速以及风偏角条件下，斜拉索振动响应、斜拉索表面水膜形态变化以及随时间变化的空气动力三者之间的关系。

1 模型

1.1 水膜运动方程

如图1(a)所示：风速大小为U0，风偏角为β，其中β的变化范围为0≤β≤90°；斜拉索半径为Rc、水平倾角为α，其中α的变化范围为0<α≤90°；受到重力和空气动力的共同作用，风攻角为0°。在斜拉索上取A-A断面，以拉索圆心为原点建立极坐标系(er,eθ)。假设拉索表面有一层连续的水膜，在任意θ角处，水膜的厚度为h(θ)，该截面上拉索表面水膜受力如图1(b)所示。

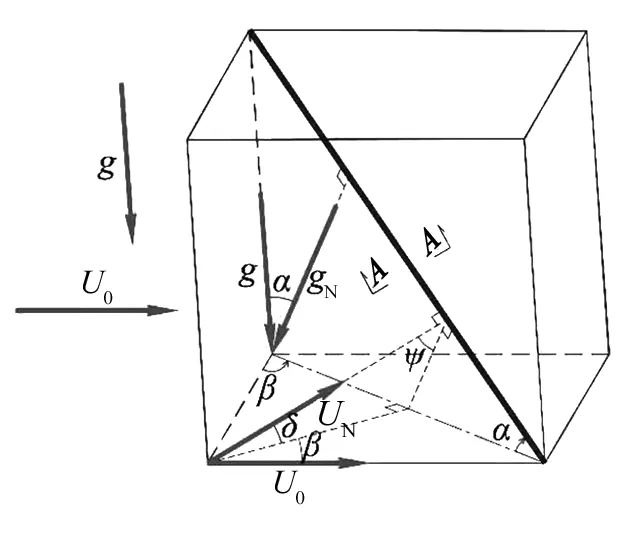
(a)斜拉索空间位置

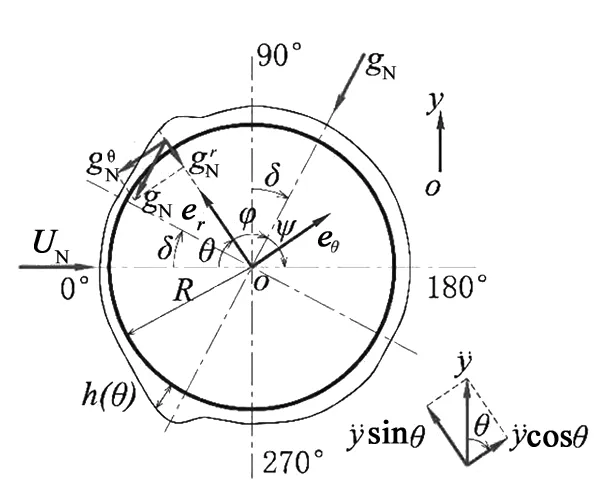
(b)斜拉索表面水膜受力图1 斜拉索模型图

忽略轴向重力分量，在该断面内的重力分量：

gN=gcosα

(1)

若只考虑二维断面内的气流作用，则斜拉索断面内的风速：

(2)

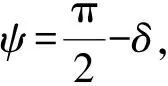
δ=arctan(sinα·tanβ)

(3)

水膜的运动方程由二维Navier-Stokes公式推导。建立极坐标系(er,eθ)，如图1(b)所示，水膜内点的坐标为(r,θ)，其中R≤r≤R+h，h为水膜厚度。将速度u表示为分量形式u=urer+uθeθ，则N-S方程可写为：

(4a)

(4b)

(4c)

根据Lemaitre等[12]的计算结果可知，水膜运动的雷诺数Reh=hu/v≈1(v为水的运动粘性系数)，式(4a)和式(4b)可写为：

ρ[gNsin(θ-δ)-sinθ]

(5a)

(5b)

方程的边界条件包括以下方面。

(1)水膜底面采用无滑移边界条件，即

ur|r=Rc=uθ|r=Rc=0

(6)

(2)水膜在与空气交界面F(r,θ,t)=Rc+

h(θ,t)-r=0处所受的应力与表面张力相平衡，即

(σg-σ)n=κγn

(7a)

σ=-pI+[μu+(u)T]

(7b)

σg=-pg(θ)I+τg

(7c)

式中：γ为水在空气中的表面张力系数，σ和σg分别为水膜和空气的应力张量，I为单位向量，pg为水膜表面所受空气压力，τg为空气粘滞力张量；n为水膜与空气交界处的法向向量，κ为水膜表面的曲率。

除了满足以上2种边界条件之外，拉索表面水膜与空气的交界面还满足自由界面F(r,θ,t)=Rc+h(θ,t)-r=0的连续条件，即水膜在与空气交界面处满足

(8)

将边界条件和式(8)带入方程(5a)、(5b)和(4c)中可得水膜运动方程：

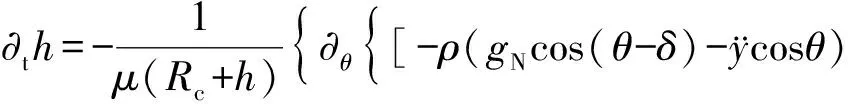
(9)

1.2 斜拉索振动方程

图2为斜拉索A-A断面受力图。设拉索质量为M，在二维模型中为单位长度上的质量，阻尼为c，刚度为K，阻尼比为ξ0，自振圆频率为ω0，根据单自由度振动理论在横风向(y轴方向)建立拉索运动方程：

(10)

式中Fy为横风向的拉索升力，按下式计算：

(11)

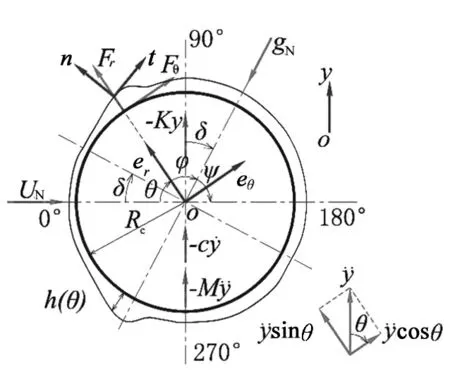
图2 斜拉索断面受力

水膜底面的应力张量为：

σ0={-pI+μ[u+(u)T]}|r=R

(12)

式中I为单位向量，则

Fr(θ)=er·σ0·er=-p+2μ∂rur|r=R

(13a)

(13b)

将式(13a)和式(13b)分别代入式(11)，即可得到升力Fy。

1.3 随时间变化的空气动力的计算

滑移理论假设拉索外表面有一层连续的水膜，因此水膜外表面与空气接触，内表面与拉索接触。水膜作为空气和拉索的媒介，在受到两者共同影响的同时也反作用于两者。已有研究结果表明[15-17]，考虑随时间变化的空气动力系数能更加准确地反映风雨激振现象。文中沿用毕继红等[18]的研究方法，采用COMSOL计算随时间变化的风压力系数Cp和风摩擦力系数Cf。在每一个时间步长内，依据该时刻水膜形态建立“类圆柱”外表面，并认为该时间步长内水膜形态采用定常流，采用SA湍流模型进行计算，计算区域设置、网格划分和边界条件设置都与文献[18]一致。

2 数值求解

2.1 水膜运动方程的求解

方程(9)为水膜运动方程，该方程为四阶偏微分方程，采用有限差分法进行求解。根据Robertson等人的研究[13]，将水膜在圆周空间上离散为128点可以保证计算精度，文中也照例设置，即相邻两个离散点与圆柱中心的连线夹角为Δθ=0.711π。时间步长取为0.001 s。水膜运动方程离散后的差分格式和差分方程可参考文献[18]。

2.2 数值求解流程

数值求解流程如图3所示。计算伊始，根据拉索和水膜的初始状态输入初始值，参数无量纲化后进入迭代过程。在迭代过程中，首先将计算结果中的水膜厚度数据读取出来；然后以此为依据在COMSOL中建立几何模型，在模型中划分网格，并根据上一步的拉索速度，设定边界条件从而建立数值模型；然后计算该时刻的水膜外表面各点处的气动力系数；再依据上一步求出的拉索加速度，求解水膜运动方程，即可获得下一时刻各点的水膜厚度；将水膜厚度变化结果代入方程(13)求解Fr(θ)和Fθ(θ)，进而求解方程(11)获得拉索升力Fy；然后将升力代入方程(10)，采用四阶Runge-Kutta法求解，可获得拉索新的位移、速度以及加速度。接下来判断是否进入最终时刻，直到计算全部结束。

2.3 基本参数选取

根据陈文礼等[10]的试验，斜拉索表面各个位置处的水膜初始厚度h0=0.2 mm，应用有限差分法求解水膜运动方程需要水膜在斜拉索表面连续分布，因此在水膜形态演变过程中，最大水膜厚度设为1 mm，最小水膜厚度设为0.02 mm。斜拉索断面上的水膜可以近似认为满足质量守恒。文中选取1×10-3s作为数值计算的时间步长。其余基本参数见表1，计算工况见表2。

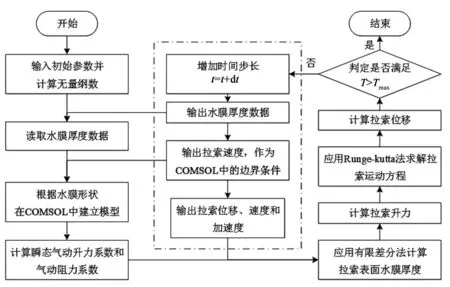
图3 计算流程图

表1基本参数

Tab.1Parametersincalculations

重力加速度g/(m·s-2)斜拉索半径R/m斜拉索倾角α/(°)斜拉索自振频率f0/Hz空气的运动粘性系数vg空气密度ρg/(kg·m-3)水的运动粘性系数v/(m2·s-1)水密度ρ/(kg·m-3)水的表面张力系数γ/(N·m-1)9.80.05300.9521.51×10-51.2251×10-610007.2×10-2

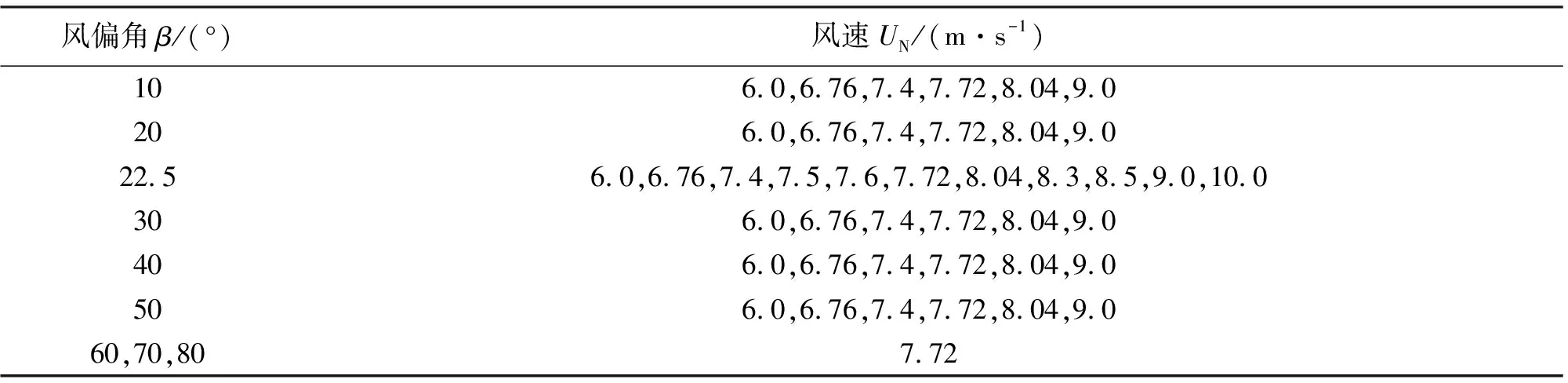
表2 数值计算工况

3 数值模拟结果

3.1 斜拉索振动响应

陈文礼等[10]在哈尔滨工业大学风洞与浪槽联合实验室中进行了人工降雨风洞试验。将风偏角为22.5°的计算结果提取出来并与试验结果相对比，结果如图4所示。其中深色线为试验结果，浅色线为计算结果。可以发现，风速过大或者过小时，斜拉索振幅都不大，在风速为7.4～7.72 m/s范围内时，斜拉索振幅大于0.08 m。这体现出斜拉索风雨激振“限速”的特点。总体上斜拉索振幅与试验结果非常接近。验证了本文中提出的斜拉索风雨激振理论模型和求解方法的准确性和可靠性。

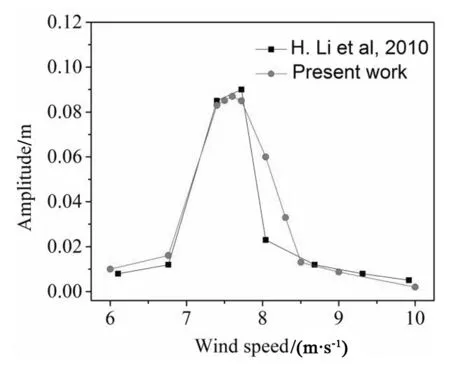
图4 各个风速下的拉索振幅与试验结果对比Fig.4 The cable amplitude comparison of calculated results and test results at every wind speed

图5给出了6个典型风速下的斜拉索振动响应时程曲线，可以发现，当风速较小时，拉索振动迅速趋于稳定，振幅很小。当风速进入激振区范围内时，斜拉索振幅初期也是比较小，经过大约30 s的能量积累之后，振幅基本稳定在最大值附近。表3是对斜拉索振动时程曲线进行频谱分析的结果，该结果表明，在风速较小以及在风雨激振范围内时，斜拉索振动主频接近斜拉索自振频率0.952 Hz，其频谱分析中的幅值逐渐增加；在风速超过激振区范围后，主频开始发生偏移，且幅值减小，说明曲线频谱特性不明显。

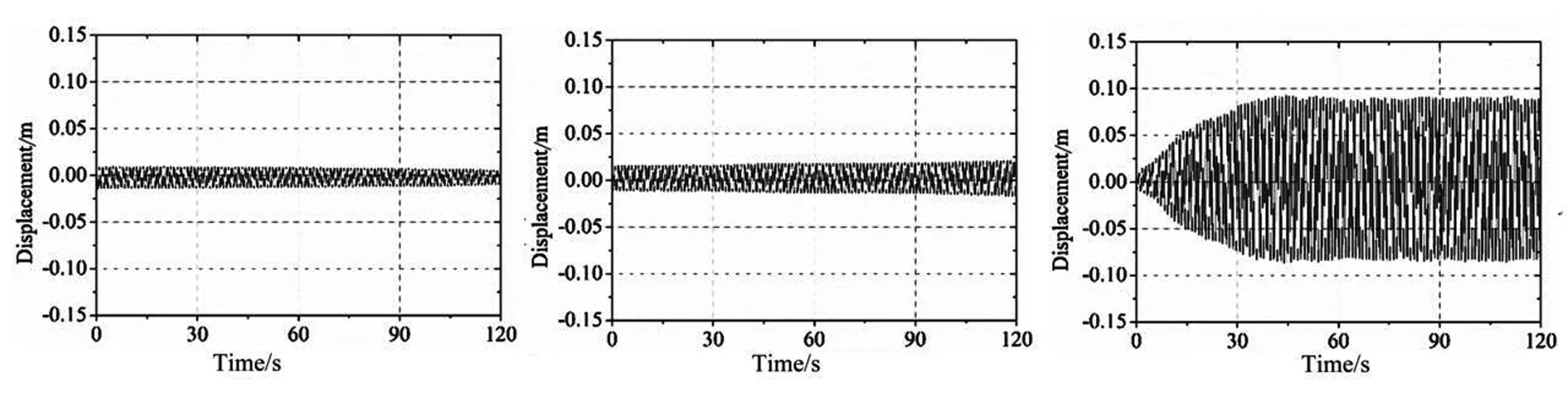
(a)UN=6.00 m/s (b)UN=6.76 m/s (c)UN=7.40 m/s

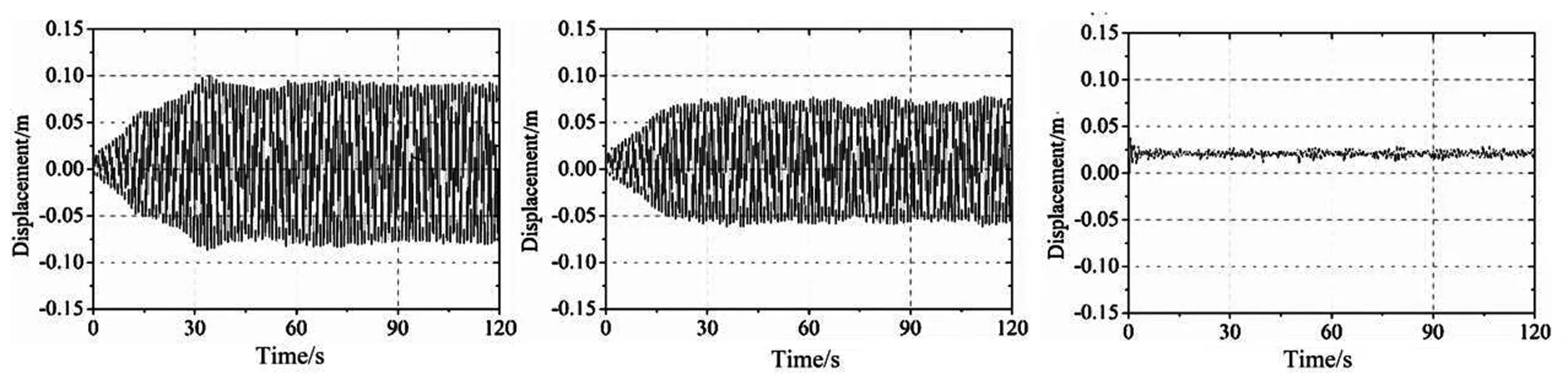
(d)UN=7.72 m/s (e)UN=8.04 m/s (f)UN=10.00 m/s图5 六个风速下的拉索振幅时程曲线Fig.5 The time history of cable vibration at six wind speeds

表3斜拉索振动主频(UN=7.72 m/s)

Tab.3Thedominantfrequencyofcablevibration(UN=7.72 m/s)

风速/(m·s-1)6.06.767.47.57.67.728.048.38.59.010主频/Hz0.9890.9890.9890.9890.9890.9890.9890.9891.033无无幅值/(°·Hz-1)0.0120.0150.0740.0740.0740.0750.0530.0280.003无无

图6给出的是风速在6.00 m/s到9.00 m/s的范围内，斜拉索振幅随风偏角的变化趋势，可以发现风偏角为22.5°，风速为7.72 m/s时的振幅最大。当风速为6 m/s和9 m/s时，风偏角在10°～50°变化时，斜拉索振幅都很小。这说明相同风偏角的情况下，随着风速改变都是先增大后减小，风偏角的改变对风雨激振区间影响不大。图7显示的是风速为7.72 m/s时，斜拉索振幅随风偏角改变的变化规律。其先增大后减小的特征明显，在风偏角为22.5°时，斜拉索振幅最大，接近0.1 m。

图6 不同风偏角下的斜拉索振幅Fig.6 The amplitudes of the cable vibrations at different wind yaw angles

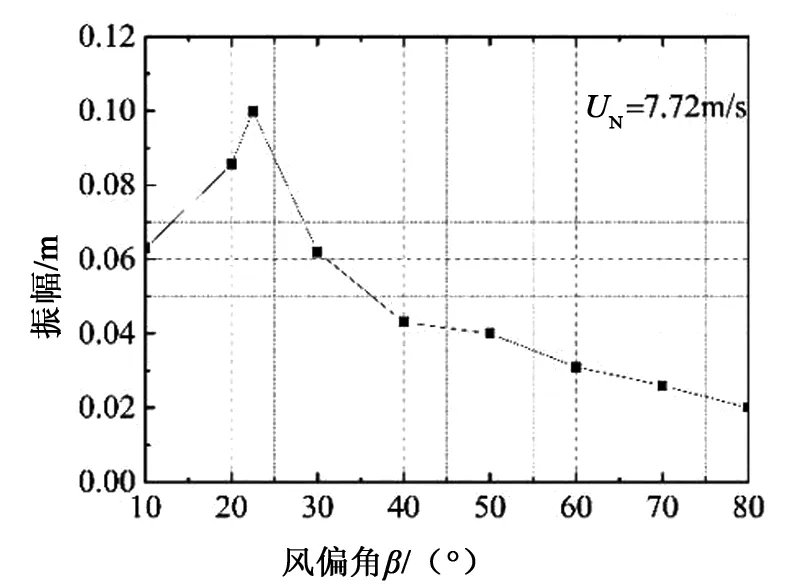
图7 风速为7.72m/s时，斜拉索振幅随风偏角的变化规律Fig.7 The variation of the amplitude of cable vibration with the wind deflection at the wind speed of 7.72m/s

3.2 上水线形态变化

图8显示的是不同风速以及风偏角条件下的上水线厚度。由图8可以发现，在风偏角相同的条件下，上水线厚度随风速增加而增大；在风速不变的情况下，上水线厚度随着风偏见增加而减小。这个规律与斜拉索振动响应规律有较大不同。为分析其原因，对上水线厚度变化时程进行频谱分析，并将风偏角在10°～50°、风速在6.00～9.00 m/s范围内的主频总结于表4中。由表4可以发现，在风速小于等于7.72 m/s范围内时，上水线厚度变化主频均为0.989 Hz，接近斜拉索自振频率，而当风速进一步增加以后，上水线主频逐渐偏离斜拉索自振频率。图9显示的是风偏角为22.5°时，3个典型风速下的斜拉索表面水膜形态演变规律。由图9可以发现，在风速为6.00 m/s时，斜拉索表面并未形成明显上水线。当风速增加到7.72 m/s，斜拉索振动稳定后，上水线在斜拉索表面周期性地形成和消失，其演变频率与斜拉索自振周期相接近。当风速增大到10.00 m/s后，上水线依然会形成，且最大水膜厚度显然比风速为7.72 m/s时更大，但同时可以发现，上水线形态杂乱，其周期性并不明显。

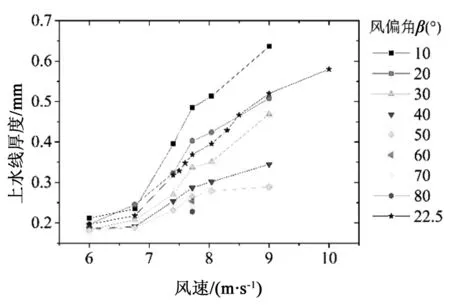
图8 不同风速以及风偏角条件下的上水线厚度Fig.8 Thickness of water film at different wind speeds and wind deflection angles

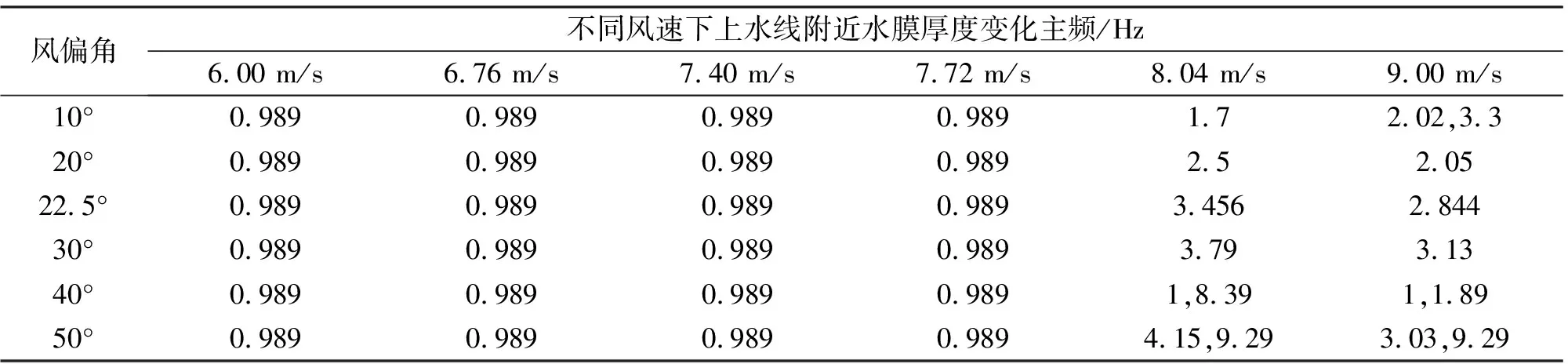
表4 上水线附近水膜厚度变化主频

(a)UN=6.00 m/s (b)UN=7.72 m/s (c)UN=10.00 m/s图9 3个典型水膜形态变化Fig.9 Three typical water film evolutions

3.3 斜拉索表面升力变化

图10是各个工况下的斜拉索表面升力幅值。由此可知：斜拉索表面升力随风速增加呈增大趋势；在风速不变的前提下，斜拉索升力随风偏角增大而减小。这是由于风偏角增加，断面内风速会减小，导致气动力减小，进而引起斜拉索升力下降。升力主频规律在表5中给出，由表5可知：风速较小以及风雨激振发生时，各个工况中升力变化主频均接近斜拉索自振频率；风速较大时，升力主频逐渐偏离斜拉索自振频率，这也是斜拉索振动主频偏移自振频率的主要原因，因为此时斜拉索受迫振动效果更明显。而斜拉索表面升力偏移斜拉索自振频率的原因是上水线运动主频逐渐消失。

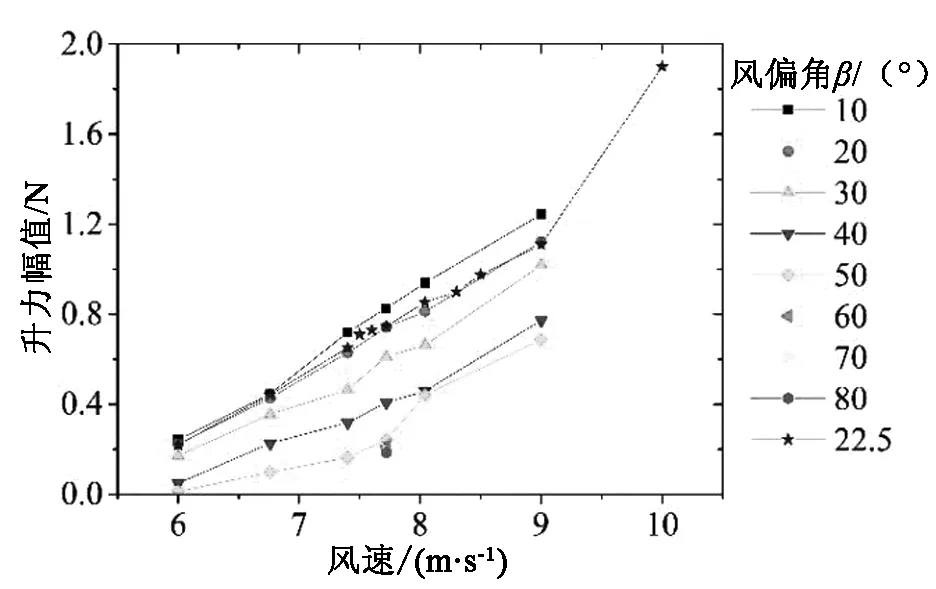
图10 各个工况下的斜拉索表面升力幅值Fig.10 Lift on the cable surface at every case

表5 不同风偏角时的升力主频

3.4 斜拉索和水线的双向耦合作用分析

由式(9)可以看出，斜拉索表面水膜运动同时受到斜拉索振动和空气动力的影响。当风速较小时，斜拉索振动对水膜运动的影响是主要的，而水膜运动对于斜拉索振动反馈作用相对较小，因此斜拉索表面受到的升力(由于水膜运动产生)较小，此时斜拉索振动类似自由振动。这也是斜拉索表面水膜厚度变化主频接近斜拉索自振频率的原因。随着风速的增大，水膜运动逐渐剧烈，水膜运动对斜拉索振动的作用也逐渐增加，但由于此时水膜运动主频依然接近斜拉索自振频率，因此此时水膜与斜拉索发生了同频谐振，导致斜拉索振幅大幅增加，风雨激振由此产生。当风速增大到激振区范围外时，水膜运动对于斜拉索振动的影响成为主要方面，由于此时斜拉索表面水膜在空气动力作用下变化剧烈，水膜形态杂乱，其周期性已不再明显。虽然此时上水线厚度比之前更大，但由于水膜与斜拉索之间的同频谐振现象已经消失，斜拉索振幅并未随着升力幅值的进一步增加而增大，反而逐渐减小，斜拉索逐渐退出风雨激振状态。

4 结论

(1)不同风偏角的条件下，随风速增加，斜拉索振幅都是先增加后减小的趋势。风偏角的改变对风雨激振的激振区间范围影响不大。

(2)在激振区间内，斜拉索振幅随风偏角的增加呈现先增加后减小的趋势，在风偏角为22.5°左右时，斜拉索振幅最大。

(3)相同风速下，随着风偏角的增加，上水线厚度以及升力幅值呈减小趋势。风偏角不变时，上水线厚度以及升力幅值均随风速增加而增大，风速超过激振范围外后，两者主频均逐渐偏离斜拉索自振频率。

(4)斜拉索与上水线之间的同频谐振是斜拉索风雨激振产生的主要原因之一。