非均质边坡稳定性有限元强度折减影响因素分析
马 伟
(山东农业大学勘察设计研究院,山东 泰安 271000)
1 引 言
土石坝、堤防、水库库岸等水利工程中存在着大量的边坡问题。边坡一旦失稳破坏,将造成重大的人员伤亡和财产损失[1]。因此,边坡稳定性分析一直是土石构筑物工程中的重要研究领域。近年来,将强度折减法和有限元结合应用于边坡稳定性分析已受到了越来越多的关注。强度折减有限元法克服了传统极限平衡法的诸多缺点,能考虑土体的非线性本构关系,满足力的平衡条件,模拟复杂的边界条件和多种材料;不仅能直观地得出边坡的应力、应变、特征点位移、塑性区分布等参数值及相应的云图分布,而且能直接得到一个物理意义明确的定量评价边坡稳定性的安全系数。
但就目前而言,在强度折减有限元计算中,单元类型、网格大小的选择,初始地应力考虑与否,边坡失稳评价标准的选取等都会对最后的计算结果造成影响;岩土体的黏聚力、内摩擦角、重度、弹性模量、泊松比以及剪胀角等材料参数同样会对安全系数的计算产生影响。
针对均质边坡的研究较多。万少石等[2]讨论了单元类型、网格大小对安全系数计算精度的影响,各种失稳判据的一致性、土体材料参数和坡角对边坡破坏模式的影响,得出了一些有益的结论。王栋等[3]通过比较计算认为单元类型应选四边形二阶单元。徐文杰等[4]讨论了初始地应力对有限元强度折减计算结果的影响。薛雷等[5]对非均质边坡稳定性中强度折减的范围进行了研究,认为应对整个区域进行折减。张鲁渝等[6]讨论了坡高、坡角、黏聚力、摩擦角对强度折减有限元法计算精度的影响,并给出了提高计算精度的具体措施。边坡的失稳判据主要有3类:ⓐ以数值计算迭代不收敛为失稳判据;ⓑ以特征部位的位移突变为失稳标志;ⓒ以是否形成连续的塑性贯通区为失稳判据。对于上述3类失稳判据,不同学者分别从各种失稳判据的差异性和内在统一性进行了论述。
目前,将有限元强度折减应用于均质边坡的例子较多,但很少涉及非均质边坡,本文拟研究单元类型和网格大小、初始地应力、失稳判据等因素对非均质边坡强度折减的影响。
2 强度折减法基本原理
20世纪70年代,Zienkiewics首先提出了强度折减的概念,后被许多学者广泛采用,并成功地应用于实际工程中。强度折减法就是在理想弹塑性有限元计算中,通过不断折减土体的抗剪强度参数c、φ,直至边坡达到临界破坏状态,此时的强度折减系数就是边坡的稳定安全系数Fs,定义为土体实际的抗剪强度与折减后极限状况下抗剪强度的比值,通过式(1)、式(2)进行计算:
c′=c/F
(1)
φ′=arctan(tanφ/F)
(2)
式中c——土体实际的黏聚力,kPa;
φ——土体实际的摩擦角,(°);
c'——土体折减后的黏聚力,kPa;
φ'——土体折减后的的摩擦角,(°);
F——强度折减系数。
本文采用有限元分析程序进行有限元强度折减,在非均质边坡中对整个区域进行折减[7],本构模型采用Mohr-Coulomb屈服准则和非关联流动法则。
3 强度折减有限元影响因素分析
3.1 单元类型和网格大小的影响
采用强度折减有限元法分析非均质边坡稳定性时,合理地选取网格的单元类型和大小是保证强度折减计算精度的重要条件之一。本文以非均质边坡[8]为例进行强度折减有限元分析,并与简化Bishop法所得结果比较,探讨网格单元类型和大小对非均质边坡强度折减有限元计算精度的影响。
非均质边坡的剖面几何尺寸及材料分区见图1,材料特性见表1。

图1 非均质边坡的剖面几何尺寸及材料分区 (单位:m)
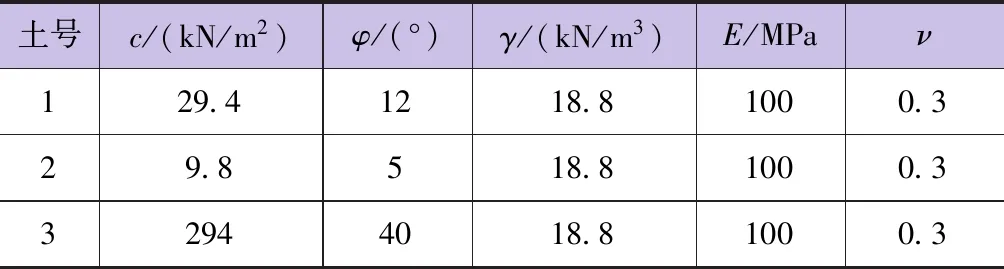
表1 非均质边坡的材料特性
为研究不同单元类型和网格大小对计算精度的影响,分别选取了四边形和三角形的一阶、二阶单元,网格大小为0.5~8m,每隔0.5m变化,进行强度折减有限元分析,计算出了在不同单元类型和网格大小下的安全系数,网格划分采用自由划分技术。为方便讨论,以有限元数值计算不收敛为失稳判据。强度折减所得安全系数和简化Bishop法的计算结果见图2。该算例的简化Bishop法所得结果为0.43[8]。
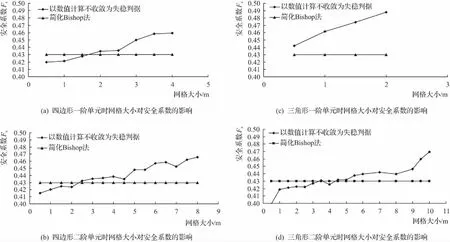
图2 单元类型和网格大小对计算精度的影响
由图2可知,不管采用何种单元类型,计算结果均随网格的稀疏而增大。与简化Bishop法所得结果相比,四边形一阶单元网格大小为0.5~3m时,误差在5%以内,当网格大小为1.5~2.5m时,误差仅在2%以内;四边形二阶单元网格大小为0.5~5.5m时,误差在5%以内,当网格大小为1.5~4.5m时,误差仅在2%以内;采用三角形一阶单元只有网格大小在0.5m时,误差在5%以内,网格变大,则得不到较好的计算精度;三角形二阶单元网格大小为1~9m时,误差在5%以内,当网格大小为2~5.5m时,误差仅在2%以内。由分析可知,采用三角形一阶单元时,计算精度得不到保证,一般不宜采用;采用四边形一阶、二阶单元时,只要网格大小合理均能保证计算结果的精度;三角形二阶单元对网格大小的要求不高,即使网格较大,仍能获得较理想的结果。由此可知,采用有限元强度折减对非均质边坡进行稳定性分析是可行的,对于四边形单元,当相对网格大小(网格大小与坡高的比值)为0.075~0.125;三角形单元,相对网格大小为0.1~0.275时,所得安全系数与Bishop法所得结果较为接近。
在非均质边坡强度折减有限元中,并不是网格划分得越小,所得结果越准确。二阶单元时,网格划分过小,不但耗费的机时很长,而且结果有时还不可用。比较一阶单元和二阶单元,二阶单元所得安全系数随网格大小变化较小,结果的稳定性好,建议采用二阶单元分析非均质边坡的稳定性。
3.2 初始地应力的影响
为了研究初始地应力对非均质边坡稳定性的影响,分别采用四边形一阶、二阶单元和三角形二阶单元,在考虑初始地应力情况下进行强度折减。根据计算结果,以数值计算不收敛为判据,不考虑初始地应力和考虑初始地应力的计算结果见表2。
由表2可知,当采用四边形单元时,考虑初始地应力时所得结果偏小,采用三角形二阶单元时,是否考虑初始地应力对计算结果没有影响,对于非均质边坡的强度折减有限元分析,初始地应力对所得结果有一定的影响,条件允许时要考虑初始地应力的影响。
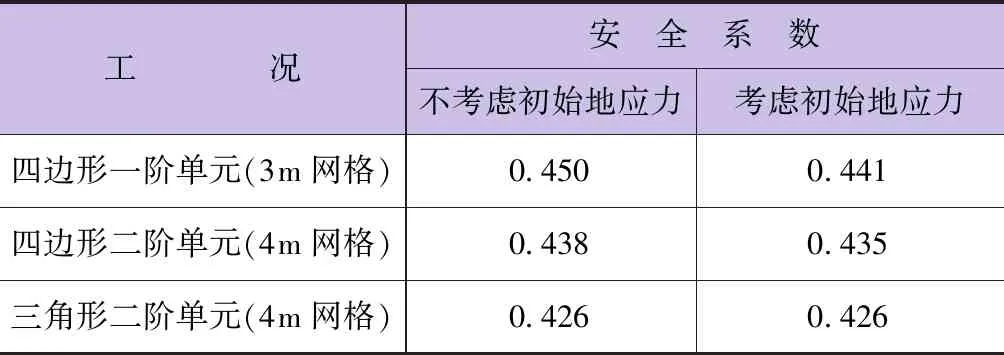
表2 安全系数计算结果
3.3 边坡失稳判据分析
如前所述,在边坡稳定性分析中应用强度折减有限元主要有3种判据,失稳判据的选取一直以来都有较大争议。本例采用三角形二阶单元4m网格进行边坡稳定分析,将坡顶点水平位移与强度折减系数的关系曲线绘于图3中,图4给出了不同强度折减系数下的塑性区分布。
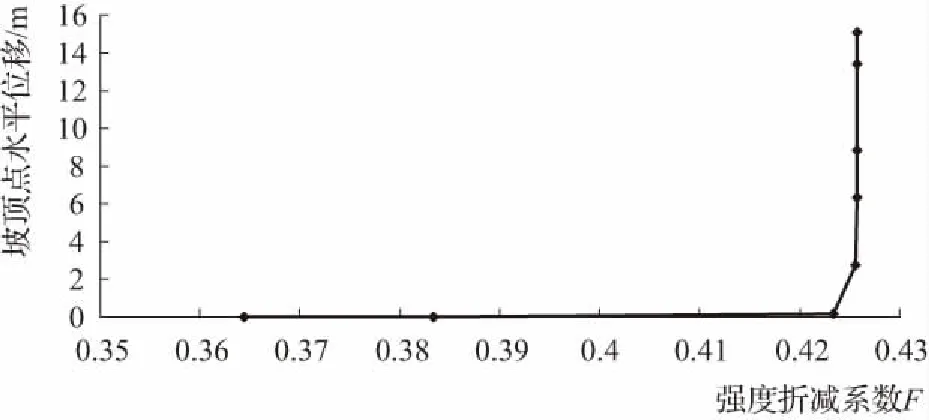
图3 坡顶点水平位移与强度折减系数的变化曲线
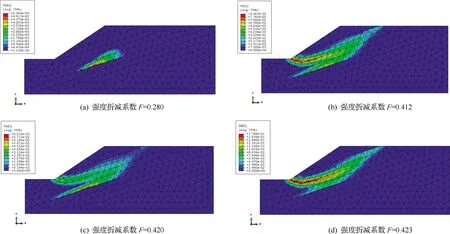
图4 塑性区随强度折减系数的变化
由图3可知,若以坡顶点水平位移突变为失稳判据,可得安全系数为Fs=0.423,对比图4中塑性区分布,当强度折减系数F=0.423时,边坡塑性区开始出现贯通现象,表征边坡正好处于极限状态。由此可得,采用特征点位移突变和塑性区是否贯通所得安全系数是一致的。若以数值计算不收敛为失稳判据,安全系数为Fs=0.426,所得结果与前两种判据的计算结果相比,数值偏大。分析边坡失稳破坏的过程,随强度折减的进行,边坡内土体开始出现塑性区并不断发展,扩大直至贯通,伴随着滑动体位移发生突变,而后进入无限制的塑性流动,继而无法承受荷载。强度折减有限元数值计算不收敛与所选取的屈服准则、所采用的计算模型、单元类型和网格大小以及设定的迭代步数等因素有关,数值计算不收敛并不一定意味着边坡达到极限破坏状态,或者可能边坡早已失稳。因此,虽然在本例中以坡顶点位移突变和以数值计算不收敛所得到的计算结果十分接近,但这与选取的单元类型和网格大小有关,并不具有普遍性。采用特征点位移突变结合塑性区贯通作为失稳判据具有明确的物理意义,更能真实反映边坡的稳定性。
4 算例验证
选取澳大利亚计算机应用协会(ACADS)对边坡稳定分析程序调查时使用的一个考核题[9]。边坡的剖面几何尺寸及材料分区见图5,材料特性见表3。
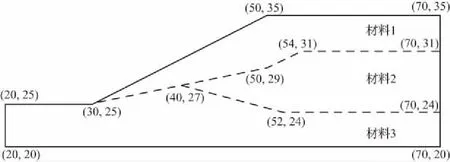
图5 算例边坡的几何尺寸及材料分区
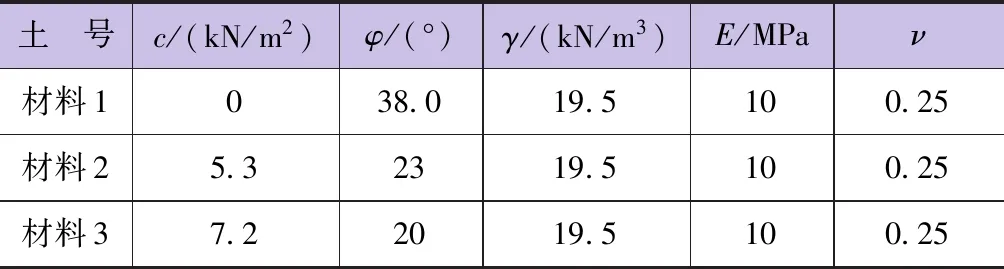
表3 算例边坡的材料特性
有限元强度折减时,采用三角形二阶单元,2.5m网格,自由划分技术。将考虑初始地应力下所得安全系数与ACADS计算结果见表4。
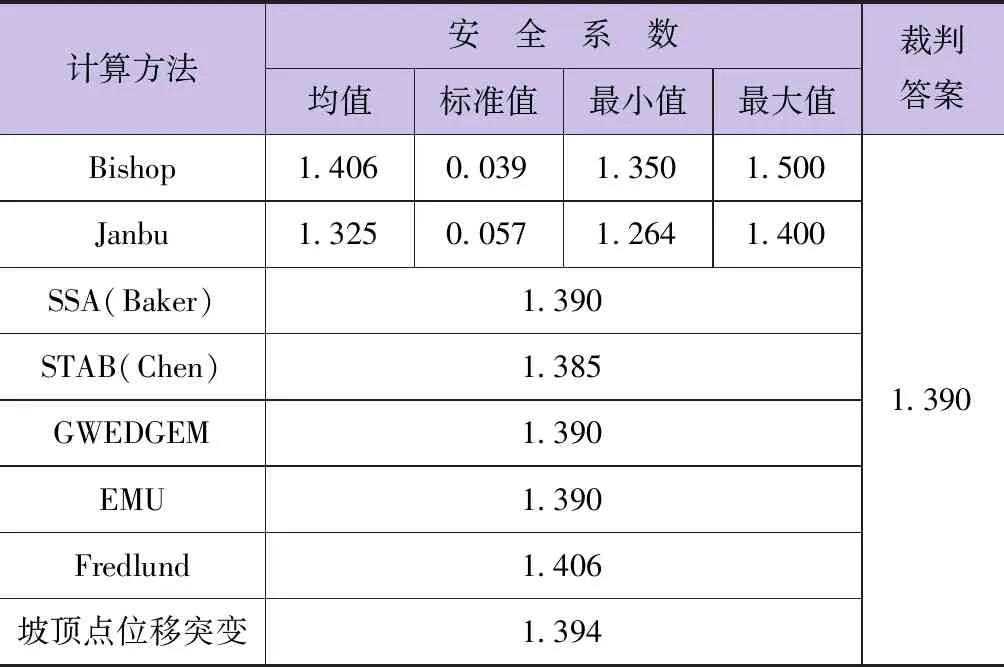
表4 计算结果汇总表
由表4可知,Bishop法所得结果较大,Janbu法所得结果较小,都偏离裁判答案。通过有限元强度折减以坡顶点位移突变为失稳判据所得结果1.394与裁判答案1.39几乎没有误差,可见本文所推荐的单元类型和网格大小以及失稳判据具有一定的合理性,对于简单的非均质边坡是适用的。但对于更为复杂的非均质边坡,结论的普遍性有待进一步研究。
5 结 语
本文将强度折减法与有限元结合应用于非均质边坡的稳定性分析。讨论了单元类型和网格大小、初始地应力、失稳判据对非均质边坡有限元强度折减计算结果的影响,得到了以下结论:
a.在非均质边坡强度折减有限元中,网格采用三角形一阶单元时计算精度差,四边形一阶、二阶单元在合理网格大小范围内满足精度要求,三角形二阶单元对网格大小要求不高,精度高。建议采用三角形二阶单元分析非均质边坡,参考的合理相对网格大小为0.1~0.275。
b.初始地应力对计算结果有一定的影响,考虑初始地应力所得结果较不考虑时偏小。若条件允许,建议在非均质边坡稳定性分析中考虑初始地应力的影响。
c.分析表明,采用特征点位移突变结合塑性区贯通为失稳判据具有明确的物理意义,能真实反映边坡的稳定性。

