求解弥散峰度张量-特征值问题的自适应信赖域法

逄 勃，张 雪，曹名圆

(北华大学数学与统计学院，吉林 吉林 132013)

0 引 言

弥散峰度张量成像可以表示各种生物组织中随机分子运动偏差中的非高斯成像[1-3]，其中的关键是利用弥散峰度张量的特征值得到空间中水分子的表观峰度系数，进而有助于疾病诊断[4-5].因此，计算弥散峰度张量特征值具有重要的应用价值.

则有

(1)

1 自适应信赖域算法

由变分原理，将问题(1)转化成如下约束优化问题

(2)

问题(2)的拉格朗日函数

对于当前迭代点xk(k∈*)，fk=f(xk)，gk=g(xk)=▽f(xk)-λkxk，Bk=B(xk)=2f(xk)-λk分别是点(xk，λk)处的函数值、L(x，λ)的梯度和Hessian阵.求解约束优化问题(2)的信赖域方法就是在迭代的每一步，求解如下信赖域子问题得到搜索方向

(3)

(4)

并且λk满足

在得到子问题(3)的解，即试探步dk之后，我们可以计算实际上升量f(p(xk+dk))-f(p(xk))和预估上升量φk(dk)-φk(0)，然后利用

(5)

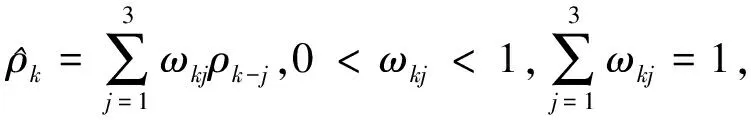
则

(6)

该策略中的比值利用3次迭代的比值加权求和得到，越新的迭代点处比值对应的加权系数越大.

算法1

步1 给定x0∈3，∈S[4，3]，且λ0=计算g0，B0.令k0.

步2 解子问题(3)得到dk.

2 算法的收敛性

为方便分析，令

则h(x)的梯度和Hessian阵分别为

引理1(ⅰ)对任意满足xTx=1，yTy=1的x和y，有

其中，M、L0和L1是正的常数.

(ⅱ)存在有界闭集Ω，对任意满足xTx∈Ω，yTy∈Ω的x和y，有

其中，L2是正的常数.

由g(x)、B(x)和▽2h(x)的光滑性和有界性显然可得引理1.

引理2考虑函数f(xk+dk)和模型φk(dk)的误差，则

证明可参照文献[6]中引理3.2.

引理3设dk是问题(4)的解，则

证明可参照文献[6]中引理3.3.

(7)

证明：反证法.假设结论不成立，存在无限集Κ⊂，使得

(8)

(9)

根据引理1～3和式(9)，我们有

由算法1知此时Δk+1单调非减，与式(8)矛盾.因此，式(7)成立.证毕.

定理1令序列{xk}由算法1产生，则有

(10)

证明：反证法.假设式(10)不成立，存在一个常数ε>0，对所有k∈，有

.

(11)

由式(10)，对充分大的k有ρk≥ω0.结合式(5)、引理3和式(11)，得

f(xk+dk)-f(xk)=ρk[φk(dk)-φk(0)]≥ω0[φk(dk)-φk(0)]≥

因为f(xk)在有界闭集Ω上单调递增且有界，有f(xk+1)-f(xk)→0(k→)，所以

这与引理4矛盾.因此，式(10)成立.证毕.

3 数值算例

本数值例子来源于福尔马林固定大鼠脊髓标本的核磁共振成像实验数据[7]，实验在CPU 2.40 GHz，RAM 2.00 GB计算机的MATLAB R2013a中运行.

w1111=0.498 2，w1112=-0.058 2，w1113=-1.171 9，w1122=0.223 6，w2233=0.151 9，

w1223=0.185 2，w1133=0.459 7，w1222=0.488 0，w1123=-0.017 1，w2333=0.763 1，

w1233=-0.408 7，w1333=0.763 9，w2222=0，w2223=-0.616 2，w3333=2.631 1和

d11=0.175 5×10-3，d12=0.003 5×10-3，d13=0.013 2×10-3，d22=0.139 0×10-3，

d23=0.001 7×10-3，d33=0.400 6×10-3(单位：mm2/s).