高效可撤销的身份基在线离线加密方案

王占君，马海英，王金华，李 燕

1.南通大学 理学院，江苏 南通 226019

2.南通大学 信息科学技术学院，江苏 南通 226019

1 引言

1984 年，Shamir 首次提出了身份基加密（Identity-Based Encryption，IBE）[1]的概念。在IBE 中，用户可以使用一个字符串（例如，家庭住址、身份证号、email地址等）表示自己的身份信息，密钥生成中心（Key Generation Center，KGC）利用该身份信息和系统主密钥为其生成用户私钥，加密者利用接收者身份信息和系统公钥加密消息。IBE 删除了传统公钥加密机制中证书验证过程，提高了加密效率。随后，学者们提出了许多实用的IBE 方案[2-4]，然而，在实际应用，用户私钥可能会泄漏、丢失或者到期，因此，IBE需要提供一种有效的成员私钥撤销机制。

针对IBE的成员撤销问题，现有的解决方案利用完全子树和子集不同方法可以实现成员撤销[5]。由于利用完全子树撤销方法，用户仅需存储较短的私钥，Boldyreva等人[6]基于该方法提出了成员撤销的IBE方案。该IBE方案利用用户身份和时间进行加密，KGC 根据最新成员撤销列表，周期性地发布未撤销用户的更新钥，使得未撤销用户利用相应的更新钥可以重构自己的解密钥。由于更新钥的工作量过大，导致KGC 可能构成系统的瓶颈。该方案[6]仅满足选择身份模型下的安全性。为了提高系统的安全性，文献[7]提出适应性安全的可撤销IBE 方案，文献[8-10]在此基础上进一步增强系统安全，提出了抗密钥暴露攻击的可撤销IBE 方案。然而，加密过程需要执行一些椭圆曲线上的幂乘运算，很难适用于轻量级设备。

为了提高 IBE 中的加密效率，2008 年，Guo 等人提出了身份基在线离线加密方案[11]，将加密过程分解为离线和在线两个阶段，离线阶段首先对大部分加密运算进行预处理生成离线密文，在线阶段利用离线密文执行少量简单运算生成密文，提高了实际加密的效率。随后，研究人员提出了一系列高效的身份基在线离线加密方案[12-16]和属性基在线离线加密方案[17-18]。然而，现有的身份基在线离线加密方案都不能实现用户撤销的功能。

本文提出了一种高效的可撤销成员的身份基在线离线加密。利用完全子树方法实现用户的撤销，首先，生成一颗完全二叉树，每个节点指定一个一次多项式f(x)=ax+1，利用该多项式将1 分解成两个份额f(1)和f(T)，其中，T为时间且大于1，利用份额f(1)来生成用户的身份私钥，利用f(T)来生成用户的更新钥。密钥生成中心周期性的发布更新钥，任意非撤销用户可以重构自己的解密钥。由于所有撤销用户都拥有相同的份额f(1)，其联合起来也不能重构解密钥，从而该方案可以抵抗联合攻击。为了减轻轻量级设备加密的负担，利用在线离线技术，将加密过程分解为离线阶段和在线阶段。在得知消息和接受者身份前，离线阶段执行大部分的加密工作。一旦得知消息和接受者身份之后，轻量级设备利用离线密文经过少量简单运算即可快速生成密文。特别地，离线阶段可在空闲时间利用高性能计算机执行。与相关知名方案相比，本文方案不仅提高了KGC 生成更新钥的效率，而且极大地减轻了轻量级设备的加密负担。

2 双线性对和DBDHI假设

双线性对：设G和GT都是素数p阶的循环群，g是群G的生成元，e:G×G→GT是一个映射，且满足：（1）双线性，对∀u,v∈G,β,δ∈Z，则e(uδ,vβ)=e(u,v)δβ；（2）非退化性，e(g,g)≠1；（3）可计算性：对 ∀u,v∈G，可在多项式时间内计算e(u,v)，则称e为一个双线性对。

2(l+1)-DBDHI 假设：设g是群G的生成元，x∈，给定一个2(l+2)元组，则任意多项式时间算法A判定T=e(g,g)1/x或T是GT中的随机元素的优势都是可以忽略的。

3 RIBOOE定义和安全模型

一个可撤销成员的身份基在线离线加密（RIBO0E）方案由初始化（Setup）、私钥生成（Genkey）、更新钥生成（Updatekey）、解密钥生成（Derivekey）、离线加密(Encoff)、在线加密 (Encon)、解密（Dec）、撤销（Revoke）算法构成。

Setup（λ，Nmax）→PP,MK,RL,ST。KGC 运行初始化算法，输入安全参数λ和用户最大个数Nmax，输出系统主密钥MK，公共参数PP，撤销列表RL，状态ST。

Genkey(ID,MK,ST,PP)→SKID，ST′。KGC运行私钥生成算法，输入身份ID、管理员密钥MK，状态ST和公共参数PP，输出ID的私钥SKID和更新的状态ST′。

Updatekey(T,PP,MK,RL,ST)→UKT,R。KGC运行更新钥生成算法，输入时间T、公共叁数PP、系统主密钥MK、撤销列表RL状和态ST，输出T时刻的更新钥UKT,R其中R为T时刻的撤销身份集合。

Derivekey (SKID,UKT,R,PP)→DKID,T/⊥。用户运行解密钥生成算法，输入私钥SKID，更新钥UKT,R和公共参数PP，输出解密密钥DKID,T或失败符号⊥。

Encoff(PP)→CToff。用户可以利用高性能设备在空闲时间运行离线加密算法，输入公共参数PP，输出离线密文CToff。

Encon(PP,ID,T,M,CToff)→CTID,T。用户利用轻量级设备运行在线加密算法，输入公共参数PP、身份ID、时间T、消息M和离线密文CToff，输出密文CTID,T。

Dec (CTID,T,DKID',T',PP)→M/⊥。接收者运行解密算法，输入密文CTID,T、解密钥DKID',T'和公共参数PP，当ID=ID′且T=T′时，输出消息M，否则输出失败符号⊥。

Revoke(ID,T,RL,ST)→RL′。KGC 运行撤销算法，输入身份ID、时间T、撤销列表RL和状态ST，输出更新后的撤销列表RL′。

RIBOOE的安全性由攻击者A和挑战者C之间的游戏来定义如下。

开始：A提交挑战身份ID*、挑战时间T*、T*时刻的撤销列表RL*给挑战者C。

初始化：挑战者C运行Setup算法，生成系统主密钥MK、撤销列表RL、状态ST、公共参数PP，并将PP发送给敌手A。

阶段1 敌手A可以适应性地询问如下3个预言机。

（1）私钥生成预言机OSK（·），敌手A 提交身份ID给C，C 运行Genkey(ID,MK,ST,PP)算法，返回SKID给A。

（2）更新钥生成预言机OUK（·），敌手A 提交时间T给C，C运行Updatekey(T,PP,MK,RL,ST)算法，返回UKT,R给A。

（3）撤销预言机ORev（·，·），敌手A提交身份ID和时间T给C，C 运行Revoke(ID,T,RL,ST)算法，并返回新的撤销列表RL′给A。如果敌手A 询问过，则C必须在T*时刻之前撤销掉用户ID*。

挑战：敌手A提交两个长度相等的消息M0，M1给C，C随机选择μ∈{0,1}，运行Encon(PP,ID,T,M,CToff)并将，返回给A。

阶段2 与Phase1相同。

猜测：A输出μ的猜测值μ′，如果μ′=μ，则称A赢得该安全性游戏。

敌手A的优势AdvRIBOOE=|Pr[μ=μ′]-1/2|。如果任意多项式时间敌手A 赢得上述游戏的优势都是可以忽略的，则称RIBOOE 在选择撤销身份列表（Selective-Revocation-List）模型下是安全的。

4 RIBOOE方案

本文方案利用完全子树方法撤销用户。首先生成一棵完全二叉树，每个节点指定一个一次多项式f(x)，使得f(0)=1。每个用户被指定到一个叶子节点，获得从其叶子节点到根节点路径上每个节点处的身份私钥。利用X=e(g,g)s加密消息。给定T时刻的撤销用户集合R，KGC生成非撤销用户的覆盖集合，为覆盖集合中的每个节点生成更新钥，使得未撤销用户利用更新钥可以计算Xf(T)，利用身份私钥计算Xf(1)，由于f(x)为一次函数，利用Xf(T)和Xf(1)可以算出Xf(0)，可以成功解密密文。特别地，撤销用户仅能计算Xf(1)，即使任意多个撤销用户联合起来也得不到f(x)上的其他点，不能重构函数f(x)，所以，无法获知f(0)的值，导致撤销用户解密失败。因此，本文方案满足抗联合攻击性。

Setup(λ,Nmax)：该算法输入安全参数λ和用户最大个数Nmax，生成素数p阶的双线性群e:G×G→GT，令g为G的生成元。随机选择，计算，，生成存放(ID,u)的用户列表UL，存放(u,fu(x))的函数列表FL。设M为消息空间，|M|=nM，选择Hash 函数，然后，生成一棵完全二叉树BT，使其至少有Nmax个叶子节点。对该树的任意叶子节点u，随机选择一个一次函数fu(x)，使得fu(0)=1，并存放(u,fu(x))到FL。最后，输出系统主密钥MK=(y1,y2,FL)、撤销用户列表RL、状态ST=(BT,UL) 和公共参数PP=(g,Y1,Y2,e(g,g),H1,H2)。

Genkey(ID,MK,ST,PP)：该算法输入身份ID、系统主密钥MK，状态ST和公共参数PP。首先，选择一个未使用的叶子节点u，将ID指定给叶子节点u，并保存该元组(ID,u)到UL中。然后，对于任意节点z∈Path(u)，检索函数列表FL={(u,fu(x))|∀u∈BT}，计算：

最后，输出更新的状态ST和用户私钥SKID={Path(u),。

Updatekey(T,PP,MK,RL,ST)：该算法输入时间T、公共叁数PP、系统主密钥MK、撤销列表RL和状态ST。首先利用RL定义T时间的撤销用户集合R，即如果存在 (ID′,T′)∈RL且T′≤T，则ID′∈R，根据用户列表UL定义撤销集合索引RI，得到撤销用户的覆盖集合CVRI。然后，对任意z∈CVRI，计算：

最后，输出更新的状态和更新钥UKT,R={CVRI,{Ez}z∈CVRI}。

DeriveKey(SKID,UKT,R,PP)：该算法输入SKID={Path(u),{Dz}z∈Path(u)} ，UKT,R={CVRI,{Ez}z∈CVRI} ，如果ID∉R，由完全子树方法得z∈Path(u)∩CVRI，得到解密钥：

否则输出⊥。

Encoff(PP) ：该算法输入公共参数PP，随机选择s,δ,β∈Zp，计算R=e(g,g)s，R0=H2(R)，R1=(Y1gδ)ss，R2=(Y2gδ)s，输出离线密文CToff=(R0,R1,R2,s,δ,β)。

Encon(PP,ID,T,M,CToff)：该算法输入公共参数PP、身份ID、时间T、消息M和离线密文CToff，计算C=R0⊕M,C1=s(H1(ID)-δ)，C2=s(T-β)，输出密文CTID,T=(C,C1,C2,R1,R2)

Dec(CTID,T,DKID',T',PP)该算法输入密文CTID,T，解密钥DKID',T'和公共参数PP，当ID=ID′且T=T′时，则计算：

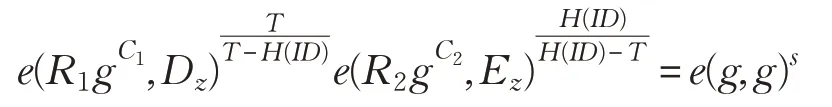
输出明文M=H2(e(g,g)s)。

Revoke(ID,T,RL,ST)：该算法输入身份ID、时间T、撤销列表RL、状态ST=(T,UL)，如果(ID,*)∈UL，输出⊥；否则将(ID,T)加入到RL中，输出更新后的撤销列表RL′。

5 安全性证明

定理如果2(l+1)-DBDHI假设成立，则本文RIBOOE方案在选择撤销身份列表模型下是安全的。

证明假定存在一个敌手A 能攻破RIBOOE 方案，则可以构造一个算法B攻破2(l+1)-DBDHI假设。

开始：A 提交挑战身份ID*、挑战时间T*和T*时刻的挑战撤销列表RL*。

（1）∀z∈FixedSubset(ID*)，随机选择y∈Zp，隐式的保存(x=H1(ID*),αy)到FL；

（2）∀z∉FixedSubset(ID*)，随机选择y∈Zp，隐式的保存(x=H1(T*),αy)到FL，注意一次函数fu(x)被两个点（0，1）和(x,αy)所确定。

B设置撤销列表RL和状态ST=(BT,UL)，随机选择π1，π2∈{1,2,…,l}，Iπ1，w1,w2,…,wπ1-1,wπ1+1,…,wl∈Zp，当i≠π1时定义，对系统运行时间T1,…,…,Tl，计算 2(l-1) 次多项式：

构造生成元：

当i{1,…,l}{π1}时，B计算：

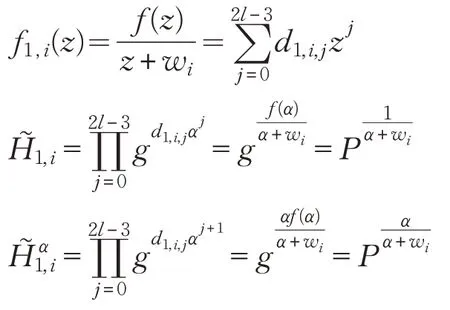
当i∈{1,…,l}{π2}时，B计算：

阶段1 A 适应性的进行哈希函数随机预言机、私钥、更新钥询问。

针对哈希函数H1的询问，假设第v次询问的身份为IDv，B设置H1(IDv)=Iv。

针对身份IDi的私钥询问，当IDi≠ID*时，首先构造点（0，1）的临时钥部件：

若(IDi,*)∈UL，从UL中下载(IDi,u)，否则随机选择u使得u≠u*∧(*,u)∉UL，并保存(IDi,u)到UL，然后得到Pathu。对节点z∈Pathu，检索函数列表(u,fu(x))，若z∈FixedSubset(ID*)，此时(x=H1(ID*,αy)：

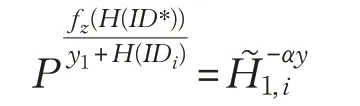
若z∉FixedSubset(ID*)，此时 (x=T*,αy)：

当IDi=ID*时，此时必有ID*∈R*，从UL中下载(ID*,u*)，得到。对，此时(x=H1(ID*),αy)：

如果敌手A 进行时间Ti的更新钥询问，当Ti≠T*时，构造点（0，1）的临时钥部件：

定义Ti时刻的撤销用户集合R，并得到覆盖集合CVRI，对节点z∈CVRI，检索函数列表 (u,fu(x))。若z∈FixedSubset(ID*)，此时 (x=H1(ID*),αy)：

若z∉FixedSubset(ID*)，此时 (x=T*,αy)：

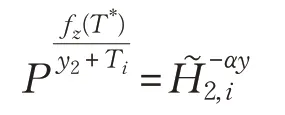
当Ti=T*时，定义T*时刻的撤销用户集合R*，并得到覆盖集合CVRI*。当ID*∈R*，FixedSubset(ID*)={Path(u*)}，CVRI*∩FixedSubset(ID*)=∅ ，当ID*∉R*，FixedSubset(ID*)=∅ ，CVRI*⋂FixedSubset(ID*)=∅ ，总之CVRI*⋂FixedSubset(ID*)=∅。对节点z∈CVRI*，检索函数列表(u,fu(x))。由z∉FixedSubset(ID*)，注意此时 (x=T*,αy)，计算：

构造更新钥为UKT,R=(CVRI,{Ez}z∈CVRI)。

挑战：A 提交两个消息M0、M1，B 随机选择μ∈{0,1}，d,m∈Zp，构造挑战密文为：B隐式的设置s=1/α，δ=H1(ID*)+α(d+1),β=T*+α(m+1)：

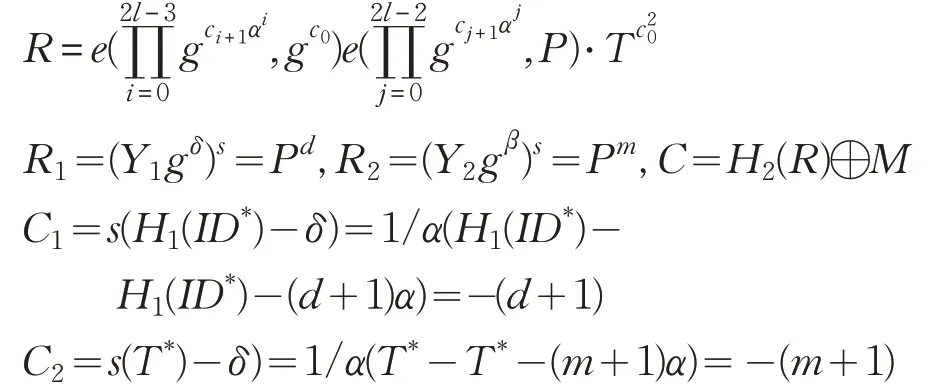
当Z=e(P,P)1/α时 ，C=Mμe(P,P)s，C1,C2,R1,R2为Mμ的密文，当Z∈GT时，C,C1,C2,R1,R2为随机消息的密文。

猜测：A 输出猜测值μ′∈{0,1}。当μ′=μ时，B 输出1，否则B输出0。

6 性能比较和实验分析

如表1 将本文RIBOOE 方案和两个相关方案在效率和功能方面进行了比较，其中，假设素数p阶的双线性群e:G×G→GT中，E表示群G中的幂乘运算，mc表示Zp中的模乘运算，r表示撤销用户的个数，Nmax表示用户最大个数。特别地，群G中幂乘的计算量远远大于Zp中模乘运算的计算量。

表1 本文方案与3个知名方案的性能比较

由表 1 可知，本文方案与 BGK 方案[6]和 JK[8]都能实现用户撤销，但BGK 的加密过程需要执行椭圆曲线上的12 个幂乘运算，轻量级设备难以在短时间内完成加密任务，且需要消耗大量电能。本文方案将加密分解成离线和在线两个阶段，加密者可以利用高性能计算机在可信环境下执行离线加密，轻量级设备仅需执行整数环上的两个模乘运算即可生成密文，整数环上的模乘运算量远远小于椭圆曲线上的幂乘运算量。因此，与BGK方案和JK 方案相比，轻量级设备运行本文方案的加密算法效率得到了极大地提高。此外，本文方案的KGC私钥更新工作量是BGK的1/7，是JK[8]的1/3。

WMW[15]提出了一种高效的可外包解密的身份基在线离线加密方案，该方案支持轻量级设备快速加密数据，但不能实现用户撤销的功能。与WMW[15]方案相比，本文方案支持用户撤销功能，尽管在线加密工作量比WMW[15]方案多执行一个整数环上的模乘运算，由于整数环上的模乘运算量极小，轻量级设备完全能够承担。性能比较表明，本文方案不仅大大提高了轻量级设备的加密效率，而且极大地减少了KGC 私钥更新的工作量，适合于轻量级设备保护用户隐私信息。

7 结束语

本文提出高效可撤销的身份基在线离线加密方案，该方案利用完全子树方法实现用户撤销功能，利用在线离线技术提高轻量级设备加密效率。基于DBDHI 假设，证明本文方案是安全的。本文方案的优势主要表现在三个方面：（1）轻量级设备的加密效率很高；（2）KGC的私钥更新工作量大大减少；（3）实现成员撤销功能。因此，本文方案非常适合于移动环境中轻量级设备保护用户隐私信息。